MATE 3. Semana del 25 al 28 marzo 2019
Bloque:
|
IV
|
Eje:
|
Análisis de la información
|
TEMA:
|
Proporcionalidad y funciones
|
SUBTEMA
|
• Cálculo y análisis de la razón de cambio
de un proceso o fenómeno que se modela con una función lineal. Identificación
de la relación entre dicha razón y la inclinación o pendiente de la recta que
la representa.
|
APRENDIZAJES
ESPERADOS
|
• Resuelve problemas que implican el uso de
las razones trigonométricas seno, coseno y tangente.
|
Intenciones didácticas: A partir de cierta información, que los alumnos construyan tablas y gráficas y que a partir de éstas, relacionen cantidades y obtengan nueva información.
1. Función de proporcionalidad directa
Definición: Se llama función de proporcionalidad directa o, simplemente, función lineal a cualquier función que relacione dos magnitudes directamente proporcionales (x,y).
Su ecuación tiene la forma y = mx ó f(x) = mx
El factor m es la constante de proporcionalidad y recibe el nombre de pendiente de la función porque, como veremos en la siguiente sección, indica la inclinación de la recta que la representa gráficamente.
Recuerda: dos magnitudes son directamente proporcionales si su cociente es constante.
Representación gráfica
Como has visto, las funciones lineales se representan gráficamente como líneas rectas. Además, como y=mx, si x=0 entonces y=0; por lo tanto la gráfica de todas las funciones lineales pasa por el punto (0,0). Para dibujar la gráfica basta con obtener las coordenadas de otro punto, dando un valor arbitrario a la x y unir ese punto con el origen de coordenadas (0,0). Si x=1, entonces y=m, por tanto m representa la variación de la y por cada unidad de x, es decir, la inclinación o pendiente de la recta. Si m es positiva, representa la cantidad que sube la y por cada unidad de x y si m es negativa la cantidad que baja. F
Definición: Se llama función de proporcionalidad directa o, simplemente, función lineal a cualquier función que relacione dos magnitudes directamente proporcionales (x,y).
Su ecuación tiene la forma y = mx ó f(x) = mx
El factor m es la constante de proporcionalidad y recibe el nombre de pendiente de la función porque, como veremos en la siguiente sección, indica la inclinación de la recta que la representa gráficamente.
Recuerda: dos magnitudes son directamente proporcionales si su cociente es constante.
Representación gráfica
Como has visto, las funciones lineales se representan gráficamente como líneas rectas. Además, como y=mx, si x=0 entonces y=0; por lo tanto la gráfica de todas las funciones lineales pasa por el punto (0,0). Para dibujar la gráfica basta con obtener las coordenadas de otro punto, dando un valor arbitrario a la x y unir ese punto con el origen de coordenadas (0,0). Si x=1, entonces y=m, por tanto m representa la variación de la y por cada unidad de x, es decir, la inclinación o pendiente de la recta. Si m es positiva, representa la cantidad que sube la y por cada unidad de x y si m es negativa la cantidad que baja. F
| 1.- Los tres hermanos Pérez asistieron al cine. El boleto de entrada cuesta $50.00: a) ¿Cuánto pagaron por las tres entradas? ________________ b) Si cada uno llevó un invitado, ¿cuánto se pagó en total para que todos entraran? _________ c) Si además asistieron los padres de los hermanos Pérez, ¿cuánto se pagó por todos? ______ A partir de la información anterior, completen la siguiente tabla: Con los datos obtenidos en la tabla anterior, tracen la gráfica correspondiente.(AQUI VA LA GRAFICA) Observen la gráfica y contesten: a) ¿Cuánto se pagará por cinco personas? _____________ b) ¿Cuánto se pagará por nueve personas? _____________ 2.- analicen la siguiente gráfica que muestra los cambios en el precio de un artículo durante los primeros meses del año, posteriormente den respuesta a las preguntas a) ¿Cuánto varió el precio del primero al tercer mes? __________________________ b) ¿Cuánto varió el precio del primero al cuarto mes? _________________________ c) Suponiendo que el incremento fue el mismo cada mes, ¿cuánto varió el precio del tercero al sexto mes? _____________________________ d) ¿Cuál es el incremento mensual del precio del artículo? _________________________ e) Si el primer mes corresponde a enero, ¿cuál es el precio del artículo en marzo? __________ f) Si el incremento fue el mismo cada mes, ¿cuál será el precio del artículo en diciembre? ________________________ g) Respecto al inciso a, encuentren el cociente del incremento en el precio entre el número de meses, es decir la “razón de cambio”. Encuentren la razón de cambio en los incisos b y c y compárenla con la del inciso a. ¿Cómo son? ________________________________________ RECUERDEN QUE LA RAZÓN DE CAMBIO SE OBTIENE POR MEDIO DE: 3.- La siguiente gráfica muestra el costo del servicio telefónico de dos compañías, con base en la información que proporciona, respondan lo que se pide. a) ¿Cuál es la razón de cambio (incremento en el costo por llamada) en cada compañía? _______________________________________________________________________ b) ¿Cuál es la relación entre las razones de cambio y la pendiente o inclinación de las rectas?________________________________________________________________________________________________________________________________________ c) ¿Por qué el costo de las 100 primeras llamadas telefónicas es el mismo en las dos compañías?____________________________________________________________________________________________________________________________________ d) ¿Cuál es el incremento en el costo de 50 a 100 llamadas en la Compañía A? ____________________________¿Y en la B?__________________________________ e) En la Compañía A, ¿el incremento en el costo de 1 a 50 llamadas es el mismo que de 51 a 100 llamadas? ___________________¿Y en la B?____________________________ Al igual que en el plan anterior es importante no confundir “incremento en el costo” y el “costo del servicio” En la compañía A el incremento en el costo de 1 a 50 llamadas es de $75.00 y el costo de las primeras 50 llamadas es de $225.00 Llena la siguiente tabla | |
Representa las funciones
4María va a la frutería y compra plátanos a 1.70 €/Kg.
| Cantidad (en Kg) | 0 | 1 | 2 | 7 | ||
| Precio (en €) | 0 | 5.1 | 8.5 |
5. Completa la tabla de valores de la función lineal y = 3x
| x | y |
|---|---|
| −3 | −9 |
| 0 | |
| 2 |
6. Relaciona cada gráfica a su expresión correspondiente que se encuentra abajo:
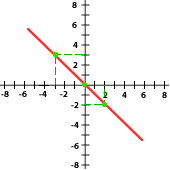
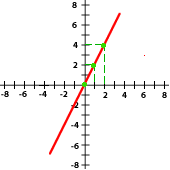
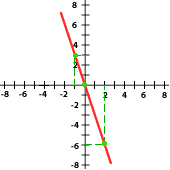
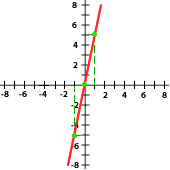
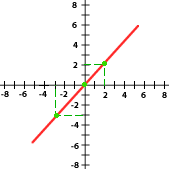
y = 2x y = −3x y = x y = −x Y = 5X
7. Indica si las pendientes de las siguientes funciones son positivas o negativas:

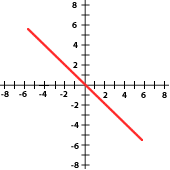
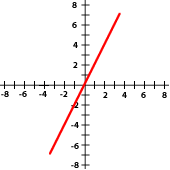
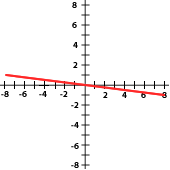
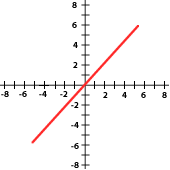
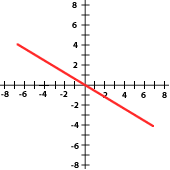
8. La cantidad de basura que se genera en una ciudad está relacionada con el número de habitantes. Completa la tabla, traza la gráfica y contesta lo que se te pide.
Habitantes (millones)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Basura
(miles de ton)
|
12.5
|
a) Cuánta basura (en kg) en promedio genera un habitante por día?
b) Cuánta basura genera por día una ciudad de un millón de habitantes?
c) Cuántos millones de habitantes tiene una ciudad que genera 12 500 toneladas de basura?
d) Qué significa la inclinación de la recta en este caso?
9. 4x+y=10
Escribe el valor faltante en la solución de la ecuación.
left parenthesis
Escribe el valor faltante en la solución de la ecuación.
left parenthesis, minus, 5, comma
Escribe el valor faltante en la solución de la ecuación.
left parenthesis








