MATE 2. Semana del 1º al 4 abril 2019
BLOQUE
|
III
|
EJE:
|
Análisis de la información
|
TEMA:
|
Proporcionalidad y funciones
|
Subtema
|
• Representación algebraica y análisis de una relación de
proporcionalidad y = kx, asociando los significados de las variables con las
cantidades que intervienen en dicha relación.
|
APRENDIZAJES ESPERADOS:
|
• Lee y comunica información mediante histogramas y gráficas
poligonales.
|
Entra al siguiente link y pasa el apunte a tu cuaderno.
Funciones Proporcionales en Tablas y Conjuntos de Pares Ordenados
Como otras funciones, las funciones proporcionales pueden ser descritas y exploradas usando tablas y conjuntos de pares ordenados. Veamos cómo las tablas de funciones proporcionales pueden ser útiles.
Mary trabaja en un puesto cerca de la granja familiar, vendiendo huevos a $1.99 por cartón los fines de semana. Cuando los clientes compran muchos cartones, ella tiene que sumar los totales con lápiz y papel, y le preocupa cometer errores. Por suerte, ésta es una relación proporcional — la salida (costo total) es igual a la entrada (número de cartones) multiplicada por una constante (el precio por cartón). Mary puede usar una función proporcional para obtener una tabla de precios.
Número de cartones
|
Precio total
|
Ahora sólo tiene que utilizar la ecuación para calcular los valores y llenar la tabla. Recuerda, la ecuación de la función proporcional es y = kx. Por lo que en éste caso, costo total = precio del cartón • número de cartones. Costo total = 1.99 • número de cartones.
Número de cartones
|
Precio total
|
1
|
$1.99
|
2
|
$3.98
|
3
|
$5.97
|
4
|
$7.96
|
5
|
$9.95
|
6
|
$11.94
|
Mary puede también escribir las entradas y salidas posibles de ésta función como pares ordenados. Un cartón de huevos cuesta $1.99 y puede ser representado como (1, 1.99). Dos cartones cuestan $3.98, o (2, 3.98), y así sucesivamente.
(1, 1.99)
(2, 3.98)
(3, 5.97)
(4, 7.96)
(5, 9.95)
(6, 11.94)
Nota que en cada par ordenado el valor de y es 1.99 veces el valor de x.
Funciones Proporcionales en Gráficas
Cuando las funciones proporcionales son graficadas, muestran algunas características distintivas — todas las funciones proporcionales son una línea recta que pasa a través del origen.
Grafiquemos la función costo/cartón que hemos estado discutiendo.
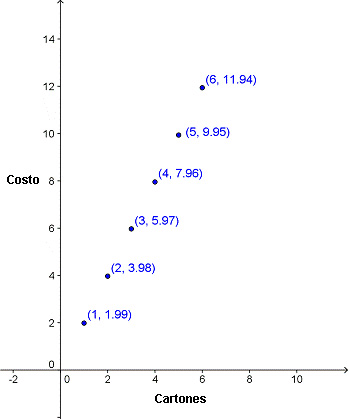
Ésta es una función discreta — está hecha de puntos individuales, porque el puesto de la granja sólo vende cartones de huevo completos. Pero podemos ver que todos los puntos están espaciados de manera uniforme, y aparentemente forman una línea recta. También podemos ver que a pesar de no estar graficado, el punto (0,0) satisface la función — el costo de 0 cartones sería de $0.
Sumario
En una función proporcional, la salida es igual a la entrada multiplicada por una constante. La constante describe la tasa con la que las variables cambian. Como ésta tasa, o constante de variación, no cambia, las funciones proporcionales tienen una ecuación y una gráfica distintivas. Todas las funciones proporcionales tienen la fórmula y = kx y forman una línea recta que termina o pasa por el origen.
TAREA PARA ENTREGAR EL JUEVES 4 DE ABRIL
1. Consideren una cisterna A y una cisterna B, que tienen la misma capacidad. La cisterna A tiene 500 litros de agua, mientras que la cisterna B esta vacía. Se abren al mismo tiempo las llaves para llenar ambas cisternas y caen, en cada una, 10.5 litros de agua por minuto.
a) Anoten las cantidades que hacen falta en las tablas.
Cisterna A
| ||||||||
Tiempo (min)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Cantidad de agua (litros)
| ||||||||
Cisterna B
| ||||||||
Tiempo (min)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Cantidad de agua (litros)
| ||||||||
b) Representen con la letra x el número de minutos y con la letra y la cantidad de agua contenida en cada cisterna y expresen algebraicamente la relación entre las dos columnas de cantidades de cada tabla.
Cisterna A: ______________________________
Cisterna B: ______________________________
c) ¿Cuántos litros de agua tendrá la cisterna A los 20 minutos de abierta la llave de llenado? _______________________
¿Cuántos litros tendrá la cisterna B en el mismo tiempo? ____________________
d) Si ambas cisternas tienen una capacidad de 2 000 litros de agua, ¿en cuanto tiempo se llenarán?
2. Para pintar un edificio de departamentos, se necesita comprar pintura de diferentes colores, si con el tipo de pintura seleccionada se cubren 24 m2 por cada 4 litros:
a) Anoten las cantidades que faltan en la tabla.
m2
|
30
|
48
|
72
|
120
|
180
|
240
|
litros
|
b)¿Qué expresión algebraica permite conocer la cantidad de litros cuando se conoce el número de metros cuadrados por cubrir? ________________
3. Completen la tabla y expresen algebraicamente cómo cambia y (longitud de la circunferencia) en función del valor de x (longitud del diámetro).
Expresión algebraica: ____________________
X
(longitud del diámetro)
|
(longitud de la circunferencia)
| |
9.42
| ||
a) Consideren la expresión y = kx, ¿cuál es el valor de k en la expresión que encontraron? ________
b) La fórmula C = p x D es la misma que y = kx, solo que con otras literales. ¿Qué valores pueden tomar C, π, D, de acuerdo con la información de la tabla?
C = ____________ π = ___________ D = ___________
4. Se sabe que la distancia que necesita un automóvil para frenar completamente es directamente proporcional a la velocidad que lleva. Al probar uno de sus nuevos modelos de autos, una compañía determinó que para una velocidad de 60 km/h el auto necesita una distancia de frenado de 12 metros .
a) Elaboren una tabla que exprese la relación entre los dos conjuntos de cantidades, velocidad y distancia de frenado. La distancia de frenado debe ir desde 12 metros hasta un metro.
b) Expresen con palabras la regla general que permite obtener las distancias de frenado a partir de las velocidades. ____________________________________________________________
c) Expresen algebraicamente la regla general que encontraron. __________________________
d) Utilicen la regla general para encontrar las cantidades que faltan en la siguiente tabla.
Velocidad km/h
|
80
|
100
|
120
|
150
|
Distancia de frenado
|
e) ¿Cuál es la velocidad que corresponde a una distancia de frenado de 20 metros?
5. ¿Cuáles de las siguientes ecuaciones representan funciones proporcionales?
Ecuación 1: 
Ecuación 2: 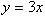
Ecuación 3: 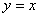
Ecuación 4: 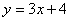
A) La Ecuación 1
B) Las Ecuaciones 2 y 3
C) La Ecuación 4
D) Las Ecuaciones 2 y 4
6. ¿Cuál es la constante de la función mostrada en la tabla?
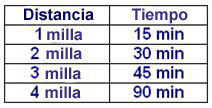
A) 15
B) 1
C) Distancia
D) Tiempo
6. ¿Cuál línea es una función proporcional?
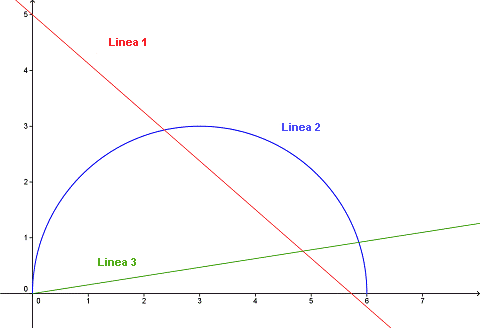
7. Haz la actividad 1 con los ejercicios 1 y 2 del link que te dejé arriba.