MATE 2. SEMANA DEL 18 AL 22 MAYO 2020

BLOQUE:
3
EJE:
FORMA, ESPACIO Y MEDIDA
TEMA:
• Magnitudes y medidas
SECUENCIA:
21. Volumen de prismas rectos
LECCIÓN:
1. Volumen de prismas rectos con base en forma de polígonos regulares
APRENDIZAJES ESPERADOS:
• Calcula el volumen de prismas y cilindros rectos.




















El prisma
Los prismas son poliedros que tienen:

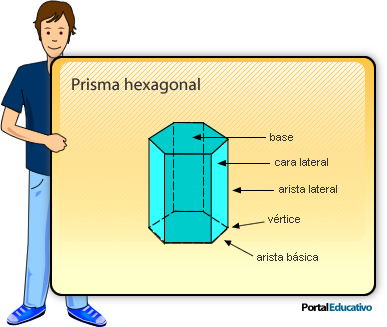
El prisma

Los cuerpos geométricos

Está constituido por dos bases poligonales e iguales y sus caras laterales son paralelogramos. Según el  número de lados de la base se le da el nombre al prisma.
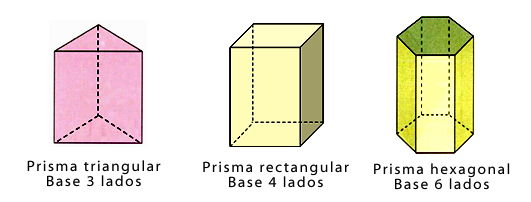
Por ejemplo:  Prismas triangular (sus bases son un triángulo), Prismas cuadrangulares (sus bases son cuadrados), Prisma pentagonal (sus bases son pentágonos), Prisma hexagonal (sus bases son hexágonos) , etc.
prisma
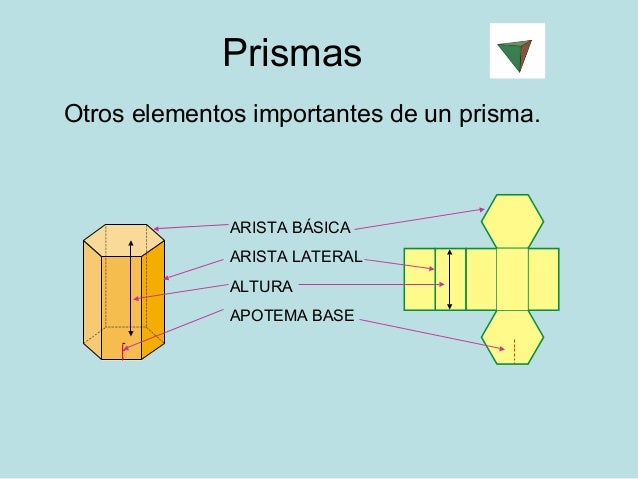
La altura de un prisma es la distancia entre las bases. 

Polígonos Regulares – Formulario de Perímetros y Áreas 0


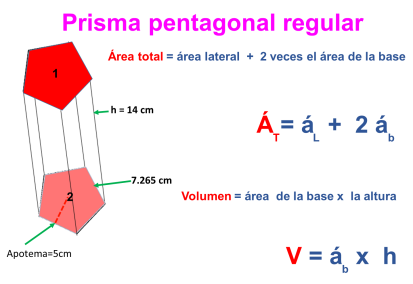
Ejemplo y fórmula volumen de un prisma recto


Un prisma recto tiene como bases dos caras planas poligonales, paralelas e iguales. Si deseamos encontrar el volumen V de un prisma recto debemos conocer el área de la base A y la altura h.
La fórmula para hallar el volumen de un prisma recto se expresa como:
V=A\cdot h
Ejemplo (prisma pentagonal):
Vamos a considerar un prisma pentagonal recto con altura de 10 centímetros, lado de 3 centímetros, y apotema de 2.064 centímetros.
Ahora, sustituimos en la fórmula y tenemos que:
V=A\cdot h
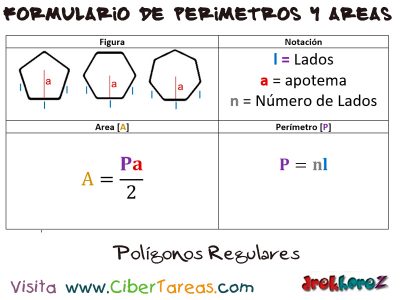
Sabemos que el área de un pentágono se calcula como el producto del perímetro P por la apotema a entre dos:
A=\frac{P\cdot a}{2}
Y el perímetro de un pentágono de lados iguales se calcula sumando 5 veces el lado l, o multiplicando el lado por 5:
P=5\cdot l
Entonces:
V=\frac{P\cdot a}{2}\cdot h
V=\frac{5\cdot l\cdot a}{2}\cdot h
V=\frac{5\cdot\hspace{0.2cm} 3\hspace{0.2cm} [cm]\cdot \hspace{0.2cm}2.064 \hspace{0.2cm} [cm]}{2}\cdot 10 \hspace{0.2cm} [cm]
V=\frac{15\hspace{0.2cm} [cm]\cdot \hspace{0.2cm}2.064 \hspace{0.2cm} [cm]}{2}\cdot 10 \hspace{0.2cm} [cm]
V=\frac{30.96 \hspace{0.2cm} [cm^{2}]}{2}\cdot 10 \hspace{0.2cm} [cm]
V=15.48 \hspace{0.2cm} [cm^{2}]\cdot 10 \hspace{0.2cm} [cm]
V=154.8 \hspace{0.2cm} [cm^{3}]
La fórmula:
V=A\cdot h
Se aplica para prismas hexagonales, heptagonales, octagonales, etc. Solo hay que recordar que el área se calcula en función del perímetro, y este último se calcula en función del número de lados

 TAREA PARA ENTREGAR EL VIERNES 22 DE MAYO

1.- Hallar  el volumen de un prisma triangular cuya base mide 10 x 43 y con una altura de 42 cm; si la  altura el prisma mide 60 cm.

2.- Hallar  el volumen de un prisma cuadrangular regular cuyo lado de la base mide 1.20 m y la altura de 4 m.

3.- Hallar  volumen de un prisma cuadrangular irregular cuya base mide 38 cm  por 21 cm y la altura del prisma es de 30 cm.

4.- Hallar el volumen de un prisma pentagonal regular cuya base mide 7.265 de lado y  5cm de apotema, y  la  altura el prisma mide 14 cm.



área_volumen_prismas18





















Entradas populares de este blog

MATE 1. Semana del 4 al 8 octubre 2019

Imagen
BLOQUE : 1 EJE: Forma, espacio y medida TEMA: Magnitudes y medidas SUBTEMA: 9. Perímetro de polígonos 10. Área de triángulos y cuadriláteros          APRENDIZAJES ESPERADOS: • Calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros desarrollando y aplicando fórmulas. Polígono regular Recordemos que un  polígono  es  regular  cuando  todos sus lados son iguales y todos sus ángulos   también  lo son. Es irregular si no cumple con estas condiciones. Nombres de polígonos regulares Tres lados………..triángulo o trígono Cuatro lados……cuadrado o tetrágono Cinco lados…….pentágono Seis lados………hexágono Siete lados……heptágono o septágono Ocho lados……octágono Nueve lados…..nonágono o eneágono Diez lados…….decágono Once lados…..endecágono o undecágono Doce lados….dodecágono Trece lados….tridecágono Catorce lados…tetradecágono Quince lados….pentedecágono
Leer más

MATE 1. Semana del 25 al 29 mayo 2020

Imagen
BLOQUE: 3 EJE: Forma, espacio y medida TEMA: Magnitudes y medidas SUBTEMA: 31. Volumen de prismas      APRENDIZAJES ESPERADOS: • Calcula el volumen de prismas rectos cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando fórmulas. Empecemos por recordar los elementos de un polígono regular. Para calcular el área de los polígonos regulares se necesita conocer su apotema. Recordemos que el área viene dada por la fórmula    Te  anexo un formulario para calcular el área  y el perímetro de varios polígonos regulares que te pueden ser de utilidad para que a su vez puedas calcular el volumen de prismas, por si no te acuerdas. Ejemplo 1. Calcula el volumen de un prisma con base rectangular, la cuál tiene de base 8cm y de altura 5cm. Sabemos que h=10 cm Dibujo                                     Fórmula            
Leer más