MATE 3. Semana del 1º al 4 de abril 2019

Bloque:	IV
Eje:	Análisis de la información
TEMA:	Análisis y representación de datos
SUBTEMA	• Medición de la dispersión de un conjunto de datos mediante el promedio de las distancias de cada dato a la media (desviación media). Análisis de las diferencias de la “desviación media” con el “rango” como medidas de la dispersión.
APRENDIZAJES ESPERADOS	• Calcula y explica el significado del rango y la desviación media.

Cómo calcular el recorrido o rango

El recorrido o rango es la diferencia entre el valor mayor y el valor menor de un conjunto de datos.

Vamos a ver un ejemplo:

Cuatro amigos han sacando las siguientes notas:

Todos tienen una nota media de 5 (lo puedes comprobar), sin embargo, unas están más dispersas que otras. Vamos a ir calculando a lo largo de la lección cada una de las medidas de dispersión.

Empezamos calculando el recorrido para el Amigo A. Su nota más alta es 7 y su nota más baja es 3, por lo tanto, su recorrido es:

El recorrido para el Amigo B es 8, para el Amigo C es 9 y para el Amigo D es 3.

Cuanto mayor sea el recorrido, más dispersos están los datos.

Desviación respecto a la media

La desviación respecto a la media es la diferencia en valor absoluto entre cada valor de la variable estadística y la media aritmética.

D_i = |x - x|

Desviación media

La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.

La desviación media se representa por D_x

Ejemplo:

Calcular la desviación media de la distribución:

9, 3, 8, 8, 9, 8, 9, 18

Calculamos la media aritmética para poder hallar las desviaciones respecto a la media

Aplicamos la fórmula de la desviación media

Desviación media para datos agrupados

Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la desviación media es:

Ejemplo:

Calcular la desviación media de la distribución:

	xi	fi
[10, 15)	12.5	3
[15, 20)	17.5	5
[20, 25)	22.5	7
[25, 30)	27.5	4
[30, 35)	32.5	2

En primer lugar calculamos la media artmética:

Incorporamos otra columna con los productos de las marcas de clase por sus frecuencias absolutas correspondientes y hacemos la sumatoria (457.5).

Por otro lado realizamos la sumatoria de las frecuencias absolutas (21)

	xi	fi	xi · fi
[10, 15)	12.5	3	37.5
[15, 20)	17.5	5	87.5
[20, 25)	22.5	7	157.5
[25, 30)	27.5	4	110
[30, 35)	32.5	2	65
		21	457.5

Añadimos otra columna a la tabla con las desviaciones respecto a la media (|x - x|)

	xi	fi	xi · fi	|xi - x|
[10, 15)	12.5	3	37.5	9.286
[15, 20)	17.5	5	87.5	4.286
[20, 25)	22.5	7	157.5	0.714
[25, 30)	27.5	4	110	5.714
[30, 35)	32.5	2	65	10.714
		21	457.5

Agregamos otra columna con los productos de desviaciones respecto a la media por sus frecuencias absolutas correspondientes (|x - x| · f_i) y calculamos su sumatoria (98.75)

	xi	fi	xi · fi	|xi- x|	|xi- x| · fi
[10, 15)	12.5	3	37.5	9.286	27.858
[15, 20)	17.5	5	87.5	4.286	21.43
[20, 25)	22.5	7	157.5	0.714	4.998
[25, 30)	27.5	4	110	5.714	22.856
[30, 35)	32.5	2	65	10.714	21.428
		21	457.5		98.57

Calculamos la desviación media

TAREA PARA ENTREGAR EL JUEVES 4 DE ABRIL

Escoge la opción que indica la desviación media de cada serie de datos:

1El número de veces que come pasta durante una semana un grupo de tres amigos:
2, 4, 3

0.67

−0.67

0

2Los litros de agua que beben al día un grupo de cuatro amigos:
2, 1, 3, 2

0.5

2.3

1

3El número de horas que Carmen ha visto la tele durante cada día de la semana pasada es:
3, 2, 3, 3, 2, 6, 3

0.81

0.78

0.18

4Las veces que se cepilla María los dientes al día durante una semana:
1, 2, 3, 3, 4, 2, 1.

1.3

0.90

2.5

5Las notas de los exámenes de matemáticas realizados durante el curso por Pablo son:
7, 5, 6, 8, 7, 8, 8, 9, 10, 10.

1.24

1.92

−1.24

6El número de horas que dedican un grupo de cuatro amigos a realizar un trabajo de investigación de Geometría:
10, 23, 12, 13

4

4.61

4.25

7Las estaturas en centímetros de un grupo de cinco amigos:
150, 160, 164, 158, 183.

9.4

7.4

8.4

8El número de veces que va al cine en un mes cada componente de un grupo de cinco amigos es:
2, 2, 2, 3, 1,

0.4

0.6

0.8

Contesta a las siguientes cuestiones:

9Las notas de matemáticas de los 26 alumnos de una clase son:

6, 2, 4, 4, 5, 5, 6, 3, 8, 6, 5, 3, 7, 6, 5, 6, 4, 4, 4, 3, 5, 5, 4, 6, 7, 4

Calcula la desviación media, redondeando a dos cifras decimales si fuese necesario:

 

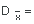
10Las faltas de asistencia de 25 alumnos de otra clase son:

0, 1, 1, 1, 3, 2, 2, 7, 1, 2, 1, 0, 0, 0, 1, 2, 1, 2, 1, 2, 0, 0, 4, 6, 7

Calcula la desviación media, redondeando a dos cifras decimales si fuese necesario:

 

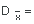
11. Encuentra la desviación media absoluta (DMA) de los datos en la siguiente gráfica de barras.

________

  chicle.

$$

$0$$1$$2$$3$$4$$5$$6$MarySophiaJadaTaraPersonaNúmero de chicleschicle por persona

12. Encuentra la desviación media absoluta (DMA) de los datos en la siguiente gráfica de puntos.

 chispas de chocolate.

$0$$1$$2$$3$$4$$5$$6$Número de chispas de chocolateChispas de chocolate en
galletas diferentes de un paquete

13. Las temperaturas máximas en una ciudad durante el mes de junio fueron:
28 ºC, 29 ºC, 28 ºC, 30 ºC, 30 ºC, 29 ºC, 30 ºC, 31 ºC, 29 ºC, 29 ºC, 30 ºC, 31 ºC, 31 ºC, 31 ºC, 32 ºC, 33 ºC, 34 ºC, 34 ºC, 35 ºC, 31 ºC, 31 ºC, 32 ºC, 32 ºC, 33 ºC, 33 ºC, 31 ºC, 32 ºC, 32 ºC, 33 ºC, 33 ºC, 34 ºC.

Calcula la moda:

Mo = 

Calcula la mediana:

Me = 

Calcula la media:

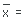
Calcula el rango:

R = 

46.96 Calcula la desviación media:

14. CALCULA LA DESVIACIÓN MEDIA 0.26 PARA LOS SIGUIENTES DATOS AGRUPADOS