MATE 3. Semana del 11 al 15 marzo 2019
Bloque:
|
IV
|
Eje:
|
Forma, espacio y medida
|
TEMA:
|
Medida
|
SUBTEMA
|
• Análisis de las relaciones entre los ángulos agudos y los cocientes
entre los lados de un triángulo rectángulo
|
APRENDIZAJES ESPERADOS
|
• Resuelve problemas que implican el uso de las razones
trigonométricas seno, coseno y tangente.
|
INTRODUCCIÓN
La utilización de las llamadas funciones trigonométricas data de la época de la antigua Babilonia. Los principios de esta rama matemáticas fueron desarrollados en su mayoría por estudios de la India, antigua Grecia y matemáticos musulmanes.Las funciones trigonométricas surgen al estudiar el triángulo rectángulo y observar que las razones (cocientes) entre las longitudes de dos cualesquiera de sus lados dependen únicamente del valor de los ángulos del triángulo
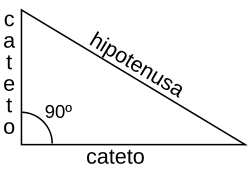
La denominación de los lados de un triángulo rectángulo son las siguientes:*
La hipotenusa (h) corresponde al lado que se encuentra opuesto al ángulo recto.
* El cateto opuesto (a) corresponde al lado opuesto al ángulo que se quiere establecer.
* El cateto adyacente (b) corresponde al lado que es adyacente al ángulo que se busca establecer.
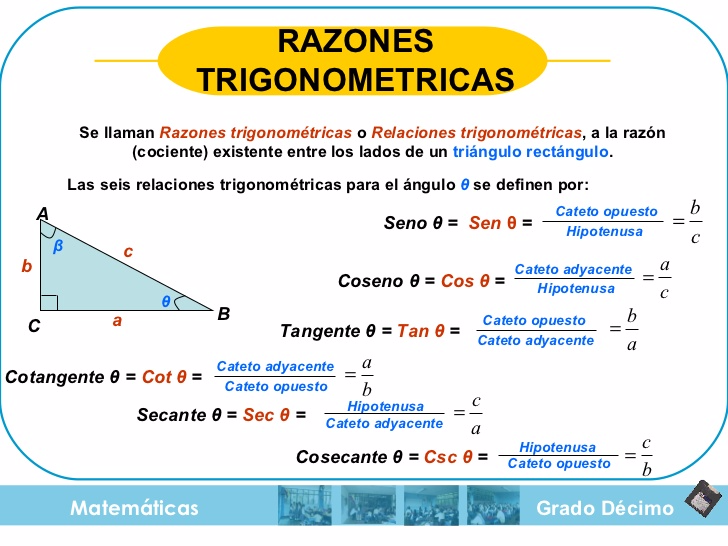
Si es un ángulo agudo de un triángulo rectángulo, se define las razones trigonométricas seno, coseno y tangente, cotangente, secante y cosecante para dicho triángulo como:
CONOCE
Ángulos de elevación y depresión
En la siguiente imagen podemos apreciar en qué consisten los ángulos de elevación y depresión:

RESUELVE Y APRENDE
1. Un árbol proyecta una sombra de 12 m de largo cuando el ángulo de inclinación del sol es de 31º. Calcula la altura del árbol.
2. Una torre proyecta una sombra de 86.9 m de largo cuando la altura del sol sobre el horizonte es de 56.5. ¿Cuál es la altura de la torre?
3. Desde un faro situado a 44 m sobre el nivel del mar, el ángulo de depresión de un barco es de 55.3. ¿A qué distancia del faro se encuentra el barco?
4.

5. Encuentra la altura de la torre y la medida del tensor que la sostiene. Utiliza para encontrar el tensor dos formas: con las funciones trigonométricas y con el teorema de Pitágoras
6. Calcular las razones trigonométricas de un ángulo agudo α, sabiendo que sec α = 4.
7-10.

11. Desde un barco vemos la luz de un faro con una inclinación de 20º y, después de avanzar 18 km en la dirección de este, se ve con un ángulo de 30º ¿a qué distancia estamos del faro?

12. Desde una determinada distancia, una bandera situada en la parte superior de un torreón se observa con un ángulo de 47º. Si nos acercamos 17,8 metros al torreón, la bandera se observa con un ángulo de 75º.
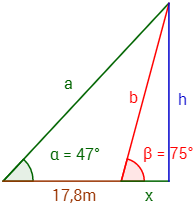
Calcular la altura a la que se encuentra la bandera.
13. Un extraterrestre diminuto pero horrible está parado en la punta del edificio Empire State (que mide 443metros de alto) y ¡amenaza con destruir la ciudad de Nueva York!
Un agente de los Hombres de Negro está parado al nivel del piso, a 18 metros del edificio, y apunta su pistola láser al extraterrestre.
A qué ángulo, en grados, debe el agente disparar su pistola láser?
Redondea tu respuesta final a la décima más cercana.
Redondea tu respuesta final a la décima más cercana.
degree
14. Los amigos de Alexa le regalaron una clase de paracaidismo para su cumpleaños. Su helicóptero despegó del centro de paracaidismo a un ángulo de

20, degree y recorrió 3, point, 4 kilómetros antes de que ella saltara en dirección perpendicular al suelo.
¿A qué distancia del centro de paracaidismo aterrizó Alexa?
Redondea tu respuesta final a la centésima más cercana.
Redondea tu respuesta final a la centésima más cercana.
kilómetros

15. Un piloto de un barco observa al vigía de un faro con un ángulo de elevación de 32º. Si la altura del faro es de 135 m, calcular la distancia del faro al barco, y la visual del piloto.
(Una observación muy válida: si fuera el vigilante del faro el que observara al piloto del barco, entonces hablaríamos de angulo de depresión)
Solución.
Observemos la figura.
16-17. . El piloto de un avión observa a un hombre en la calle de una ciudad con un ángulo de depresión de 42°, como se muestra en la figura:

Pregunta 1: Si la visual del piloto es de 15.95 km, la horizontal del piloto en ese momento es:
A. 9.52 km
B. 8.77 km
C. 11.85m
D. 11.85 km
Pregunta 2: La altura h del piloto es aproximadamente:
A. 12.85 km
B. 10.67 km
C. 19.67 km
D. 11.93 km
Puedes practicar con la siguiente página interactiva.

