MATE 2. Semana del 11 al 15 marzo 2019
BLOQUE
|
III |
EJE:
|
Forma, espacio y medida
|
TEMA:
|
Figuras y cuerpos
|
Subtema
|
• Formulación de una regla que permita calcular la suma de los
ángulos interiores de cualquier polígono.
|
APRENDIZAJES ESPERADOS:
|
• Justifica la suma de los
ángulos internos de cualquier triángulo o polígono y utiliza esta propiedad
en la resolución de problemas.
|
SUMA DE ÁNGULOS INTERIORES DE UN POLÍGONO
La suma de los ángulos interiores de un polígono depende del número de triángulos que se formen dentro de este por medio del trazo de sus diagonales desde un solo vértice.
La Fórmula empleada para determinar cuánto es la suma de ángulos interiores en un polígono es:
Donde:
n es el número de lados del polígono.
(n-2) es el numero de triángulos formados.
180° es lo que vale cada triángulo sumando sus ángulos interiores.
La regla general
Así que cada vez que añadimos un lado más (de triángulo a cuadrilátero, a pentágono, etc) sumamos otros 180°al total:
| Si es regular... | ||||
| Figura | Lados | Suma de los ángulos interiores | Forma | Cada ángulo |
|---|---|---|---|---|
| Triángulo | 3 | 180° | 60° | |
| Cuadrilátero | 4 | 360° | 90° | |
| Pentágono | 5 | 540° | 108° | |
| Hexágono | 6 | 720° | 120° | |
| ... | ... | .. | ... | ... |
| Cualquier polígono | n | (n-2) × 180° | (n-2 | |

5.- Elementos de un polígono
Observa el polígono ABCDE. Cada uno de los puntos es un vértice. En el dibujo hay 5 vértices: A, B, C, D y C. Los lados son los segmentos que componen el contorno. En este caso tenemos 5 lados: AB, BC, CD, DE y EA.
La diagonal es toda recta que une dos vértices no consecutivos. En el dibujo, de cada vértice salen 2 diagonales. En el dibujo hay 5 diagonales: AC, AD, BD, BE y CE.

TAREA PARA ENTREGAR EL VIERNES 15 MARZO
Completa la tabla siguiente
Polígono
|
Número de lados
|
Cuántos triángulos hay
|
Suma
de los ángulos internos del polígono
|
triángulo
|
|||
cuadrilátero
|
|||
pentágono
|
|||
hexágono
|
|||
heptágono
|
|||
octágono
|
|||
eneágono
|
|||
decágono
|
|||
Polígono de n lados
|
n
|
¿Cuál es la expresión que permite calcular la suma de los
ángulos interiores de cualquier polígono?______________________________________________________________
1. ¿Cuánto mide cada ángulo interior de un dodecágono
regular?___________
¿Por
qué?_______________________________________________________
2. Si la suma de los ángulos interiores de un polígono es
igual a 1620°, ¿Cuántos lados tiene el polígono?__________ ¿Cómo se llama?_______________________________________
3. La siguiente figura
muestra una parte de un polígono regular. Cada ángulo marcado con rojo mide 140º. ¿De qué polígono se trata?_______________
¿Por qué?______________________________________
4. En el centro de la plaza de mi pueblo hay
un kiosco de forma octagonal donde se presentan artistas y diversos eventos.
Quieren colocar en cada esquina un adorno y para que la base del adorno quede
justa, necesitan saber cuánto miden los
ángulos internos del piso del kiosco, que tiene forma de octágono.
¿Cuál es la expresión que permite calcular
la medida de un ángulo interno del piso del kiosco?

Ejercicio 5
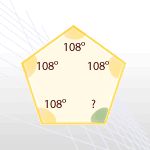
¿Qué polígono tiene sus ángulos interiores que suman 540°?
Ejercicio 6
¿Cuanto mide cada ángulo interior de un octágono regular?
7.
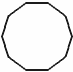
Ejemplo: ¿Cuánto mide un ángulo interno de un decágono?
 |
8 Atendiendo al siguiente dibujo escoge la opción correcta:
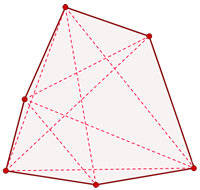
1Los segmentos del contorno del polígono se denominan ...
2Los puntos señalan...
3En el dibujo...
4La suma de los ángulos interiores de este polígono es de...
Elige la opción correcta:
5Un polígono tiene...
6Un polígono...
7Los ángulos interiores de un polígono de 5 lados suman...
8Un polígono de 7 lados tiene...
Responde a las siguientes cuestiones:
9Sabiendo que la suma de los ángulos interiores de cierto polígono es de 720°, ¿cuántos lados tiene dicho polígono?
lados.
10¿Existe algún polígono tal que la suma de sus ángulos interiores sea igual a 920°? (Sí o No)