MATE 3. Semana del 25 al 29 mayo 2020
|
BLOQUE:
|
3
|
|
Eje:
|
Análisis de datos
|
|
TEMA:
|
Probabilidad
|
|
APRENDIZAJES ESPERADOS:
|
• Calcula la probabilidad de ocurrencia de dos eventos mutuamente
excluyentes.
|
Fórmula de la probabilidad teórica
Si todos los resultados en un espacio muestra son igualmente probables, y es un evento en entonces la probabilidad teórica del evento está dada por:
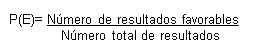
Aplicaciones de la probabilidad
Las probabilidades teóricas se aplican a toda clase de juegos de azar (lanzamiento de dados, juegos de cartas, ruletas, lotería, etc.), y aparentemente también a muchos fenómenos de la naturaleza.
Un ejemplo de ello es un fraile austriaco llamado Gregor Mendel hacia un curioso experimento con cruces de dos especies homologas de diferentes características, esta fue una de las primeras aplicaciones de la teoría de la probabilidad y de las ciencias naturales.
Eventos mutuamente excluyentes y Eventos equiprobables y no Equiprobables.
Juan, Luis y María juegan a lanzar un dado una sola vez.
Juan gana si ocurre el evento {1, 2}, Luis gana si ocurre el evento {3, 4} y
María gana si ocurre el evento {5, 6}. Se lanza el dado y sale 3, ¿quién ganó?
Dos eventos son mutuamente
excluyentes si no tienen elementos en común. En el juego anterior, los
eventos son mutuamente excluyentes.
En cambio, si se hubieran definido así:
Juan gana si sale un número par; María si es impar, y Luis si es múltiplo de 3,
los eventos no serían mutuamente excluyentes, lo que traería como
consecuencia de que si sale el 6 no haya un ganador único.
Dados dos eventos A y B de una experiencia aleatoria, se
llama la unión de A y B al evento compuesto
A U B; se dice que A U B ocurre, si
ocurre A u ocurre B, o equivalentemente si ocurre al menos uno de ellos.
La probabilidad de que ocurra la unión de A y B se encuentra
mediante la regla de la suma que establece que:
Si dos eventos son mutuamente excluyentes entonces se
cumple:
P (A U B) = P(A) + P (B)
Un juego justo es aquel en el que todos los jugadores tienen la misma probabilidad de ganar, mientras que uno injusto es aquel en el que hay una distinción entre quienes pueden ganar el juego y quienes no, por ejemplo, aquellos que dependen de quién hace el primer movimiento, como sucede en el juego del “gato”
TAREA PARA ENTREGAR EL VIERNES 22 DE MAYO
1. Un problema en el que esta regla puede usarse es el
siguiente:
Ana, Beto, Carolina y Daniel inventan un juego en el que
lanzan una moneda tres veces y definen al ganador de acuerdo con el número de
águilas que aparezcan, de la siguiente manera:
A: Ana gana si sale 0 águilas (3 soles)
B: Beto gana si sale 1 águila
C: Carolina gana si salen 2 águilas
D: Daniel gana si salen 3 águilas
En este problema se puede preguntar ¿cuál es la probabilidad de cada evento? Anoten los resultados en un cuadro como el siguiente:
Evento
|
A
|
B
|
C
|
D
|
Total
|
Probabilidad
|
1
|
¿Es justo este juego?
Vamos a cambiar el problema:
deciden los amigos dar el premio por parejas, Ana y Carolina forman un equipo y Beto y Daniel,
el otro. Calculen las probabilidades de cada equipo y
que completen la tabla siguiente:
Probabilidad de ganar del equipo de Ana y Carolina:
P(A U C) =
Probabilidad de ganar del equipo de Beto y Daniel:
P(B U D) =
¿Es justo este juego?
2. Es un juego justo?
3. Se tiran dos dados a la vez y se suman las caras que quedan hacia arriba. Cada jugador escoge un número que corresponde a la suma de los dados: 2, 3, 4, 5,..., 12. Todos tienen la mism aoprtunidad de ganar?
