MATE 1. Semana del 1 al 5 de junio 2020

BLOQUE:	3
EJE:	Forma, espacio y medida
TEMA:	Magnitudes y medidas
SUBTEMA:	32. Problemas de volumen de prismas
APRENDIZAJES ESPERADOS:	• Calcula el volumen de prismas rectos cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando fórmulas.

La "capacidad" y el "volumen" son términos que se encuentran estrechamente relacionados. Se define la capacidad como el espacio vacío de alguna cosa que es suficiente para contener a otra u otras cosas. Se define el volumen como el espacio que ocupa un cuerpo. Por lo tanto, entre ambos términos existe una equivalencia que se basa en la relación entre el litro (unidad de capacidad) y el decímetro cúbico (unidad de volumen).

Algunas equivalencias de capacidad y volumen

1 litro = 1 dm³  = 1,000 cm³

Recordemos antes los elementos del prisma.

Ejemplo 1. Realizando un despeje

¿Cuál será la altura de un prisma que tiene un área de 600 cm² y un volumen de 1800 cm³?

Fórmula                Despeje              Sustitución                                      Resultado

V= Ab · h      V= Ab · h      h = 1800 cm^{3 /} 600 cm²         h = 3 cm

             Ab · h = V

                   h = V / Ab     

Recuerda que en este caso no te están pidiendo el volumen sino la altura del prisma, por eso es necesario hacer un despeje, una vez que lo tienes solo basta con sustituir valores y realizar las operaciones.

Otro despeje que te podría ser de utilidad al momento de trabajar con volúmenes sería cuando te piden calcular el área de un prisma sabiendo los datos del volumen y de la altura

                     V= Ab · h     

             Ab · h = V

                   Ab  = V / h

TAREA PARA ENTREGAR EL VIERNES 5 DE JUNIO

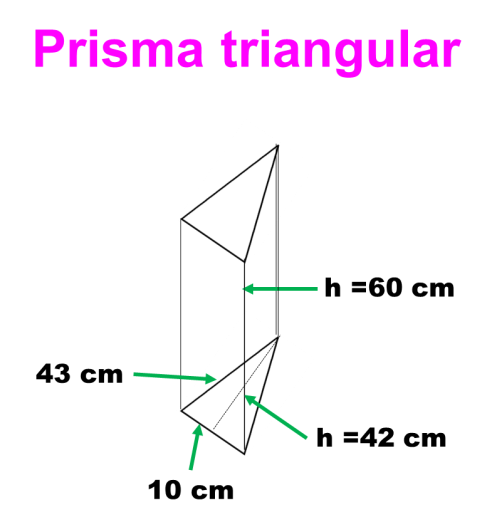
1. Calcular el volumen del siguiente prisma triangular

2.  Calcular la altura de un prisma rectangular si  le caben 2 litros y el área de la base es de 100  cm²
(Realiza primero la conversión de  los litros a centímetros cúbicos como te explican en el video) ( Checa el ejemplo donde te explican el despeje de la altura  para calcularla)

3. Sea un prisma rectangular de dimensiones conocidas, siendo los lados contiguos de la base a=3 cm y b=1,5 cm y la altura h=4 cm.

¿Cuál es su volumen?

4. Queremos hacer un tetra pack de base cuadrada de 10 cm de altura (para que  quepa en los estantes de los supermercados) y con capacidad de 2 L. ¿Cuánto cartón necesitaremos? (Sugerencia: convierte los litros a cm³ y trabajas en estas unidades)