MATE 3. Semana del 9 al 13 de marzo 2020

Bloque:	3
Eje:	Forma, espacio y medida.
TEMA:	Magnitudes y medidas
Contenido:	24. Seno, coseno y tangente
APRENDIZAJES ESPERADOS:	• Análisis de las relaciones entre los ángulos agudos y los cocientes entre los lados de un triángulo rectángulo.

Les dejo el siguiente video para que construyan su clinómetro o goniómetro y la manera de medir  o calcular alturas  de edificios, árboles, etc. TAREA: Costruye tu goniómetro y llévalo el miércoles a más tardar. Es OBLIGATORIO.  

INTRODUCCIÓN La utilización de las llamadas funciones trigonométricas data de la época de la antigua Babilonia. 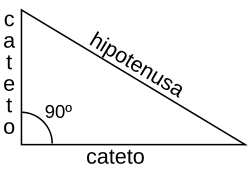Los principios de esta rama matemáticas fueron desarrollados en su mayoría por estudios de la India, antigua Grecia y matemáticos musulmanes.Las funciones trigonométricas surgen al estudiar el triángulo rectángulo y observar que las razones (cocientes) entre las longitudes de dos cualesquiera de sus lados dependen únicamente del valor de los ángulos del triángulo La denominación de los lados de un triángulo rectángulo son las siguientes:*

La hipotenusa (h) corresponde al lado que se encuentra opuesto al ángulo recto. * El cateto opuesto (a) corresponde al lado opuesto al ángulo que se quiere establecer. * El cateto adyacente (b) corresponde al lado que es adyacente al ángulo que se busca establecer.

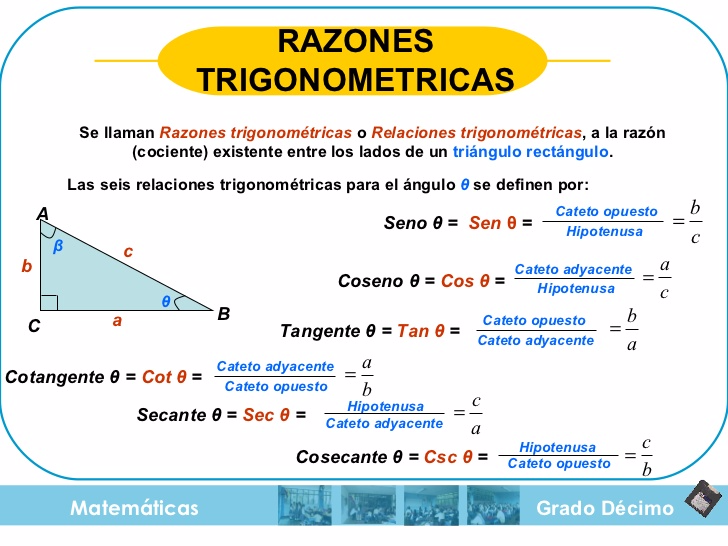
Si es un ángulo agudo de un triángulo rectángulo, se define las razones trigonométricas seno, coseno y tangente, cotangente, secante y cosecante para dicho triángulo como:

1. Unos rescatistas deben ayudar a salir a unos excursionistas que han quedado atrapado en el fondo de un barranco de 35 m de profundidad. Cuentan con una cuerda y saben que para poder colgar una canastilla con seguridad, deben tener un ángulo con la vertical de 40°. ¿Qué largo debe tener la cuerda para llegar en canastilla a los excursionistas?

$BC=$B, C, equals

Redondea tu respuesta a la centésima más cercana.

$70^{\circ}$$?$$5$$C$$B$$A$

3. AC=

A, C, equals

Redondea tu respuesta a la centésima más cercana.

$35^{\circ}$$3$$?$$C$$B$$A$

4. BC=

B, C, equals

Redondea tu respuesta a la centésima más cercana.

$65^{\circ}$$?$$7$$C$$B$$A$

5. Resolver (hallar los 3 ángulos y los 3 lados) el triángulo rectángulo ABC sabiendo que el lado b = 102.4 m y el ángulo B = 55º


6. La base de un triánguulo isósceles  mide 10 m  y el ángulo opuesto  50º. Hallar el área

7. La hipotenusa de un triángulo rectángulo mide a = 25 m y el cateto  b = 20 m. Resolver el triángulo


8. Los polígonos regulares están formados por triángulos isósceles, tantos como lados tenga el polígono. El valor de los lados iguales es el radio de una circunferencia circunscrita. Si es hexágono los triángulos son equiláteros.
Hallar el área de un pentágono regular de lado 10m.




9. SOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS • Resuelve los siguientes triángulos rectángulos, encontrando todos los datos faltantes:
1.   a=35.4ft   B=38º50´
2.   a=25.3m    A=57º42´
3.   c=9.87 km    B=34º25´42”
4.   a= 8km     b=7km
5.   a=354.2m    c= 566 m


10. Los amigos de segundo año de Danna le regalaron una clase de paracaidismo para su cumpleaños. Su helicóptero despegó del centro de paracaidismo a un ángulo de 

$20^\circ$20, degree y recorrió $3.4$3, point, 4 kilómetros antes de que ella saltara en dirección perpendicular al suelo.

¿A qué distancia del centro de paracaidismo aterrizó Alexa?
Redondea tu respuesta final a la centésima más cercana.

11. El piloto de un avión (NO es el novio de Camila, por supuesto) observa a un hombre en la calle de una ciudad con un ángulo de depresión de 42°, como se muestra en la figura:

Pregunta 1: Si la visual del piloto es de 15.95 km, la horizontal  del piloto en ese momento es:

A. 9.52 km

B. 8.77 km

C. 11.85m

D. 11.85 km

Pregunta 2: La altura h del piloto  es aproximadamente:

A. 12.85 km

B. 10.67 km

C. 19.67 km

D. 11.93 km

12. Desde un barco vemos la luz de un faro con una inclinación de 20º y, después de avanzar 18 km en la dirección de este, se ve con un ángulo de 30º ¿a qué distancia estamos del faro?  



13-16.


17. Halla la anchura del río, utilizando las medidas que se han tomado: 



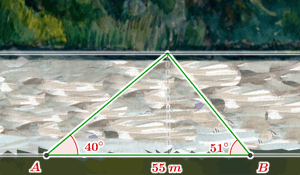
18. Dos personas separadas por una distancia de 5 km observan un avión con ángulos de 23º y 18º respectivamente. ¿A qué altura se encuentra el avión y quién se encuentra más cerca del avión?