MATE 2. Semana del 16 al 20 de marzo del 2020
BLOQUE
|
2
|
EJE:
|
Forma, espacio y medida.
|
TEMA:
|
Magnitudes y medidas
|
SECUENCIA:
|
16. Perímetro y área de polígonos regulares
|
LECCIÓN:
|
1. Perímetro y área de polígonos
|
APRENDIZAJES ESPERADOS:
|
• Calcula el perímetro y el área de polígonos regulares y del
círculo a partir de diferentes datos
|
Áreas y perímetros de polígonos regulares
- Cálculo del perímetro
Sumando las longitudes de los lados de un polígono hallaremos su perímetro.
- Cálculo del área
Para calcular el área de un polígono regular cualquiera se divide en triángulos uniendo el centro con cada uno de los vértices. La altura de cada uno de los triángulos coincide con la apotema del polígono. Se calcula el área de uno de estos triángulos y se multiplica por el número de triángulos que se han formado.
n= número de lados
Perímetro = número de lados multiplicado por longitud del lado.
El área de un polígono regular es igual al producto de su perímetro por su apotema dividido entre dos.
Apotema: segmento que une el centro del polígono con el punto medio de cada lado.
Esta fórmula permite calcular la apotema de cualquier polígono regular.
Ejemplos
Encuentra la área de la siguiente habitación:
Lo puedes hacer de dos formas:
| Método #1 | Método #2 |
Divide la figura en dos rectángulos y encuentra las longitudes que faltan. El rectángulo grande tiene un área de: 4 cm × 7 cm = 28 cm2 El rectángulo más pequeño tiene un área de: 4 cm × 2 cm = 8 cm2 Si las sumamos tenemos la área total: 28 cm2 + 8 cm2 = 36 cm2 | Dibuja dos líneas para convertir la figura en un gran rectángulo. La área del gran rectángulo es: 7 cm × 6 cm = 42 cm2 Sin embargo, un rectángulo de 2 × 3 cm no pertenece a nuestra figura original, así que tenemos que restar la área del rectángulo blanco. (2 cm × 3 cm = 65 cm2) 42 cm2 – 6 cm2 = 36 cm2 |
2. Encuentra la área de esta parte de una cancha de básquetbol:
Esta figura ya está dividida en dos: un rectángulo y un semicírculo.
Tenemos que encontrar la área de cada uno y sumarlas.
Área del rectángulo = 19 ft × 12 ft = 228 ft2
Área del semicírculo = 
Área total = 228 + 56.52 = 284.52 ft2
Ejemplo de área de un polígono irregular:
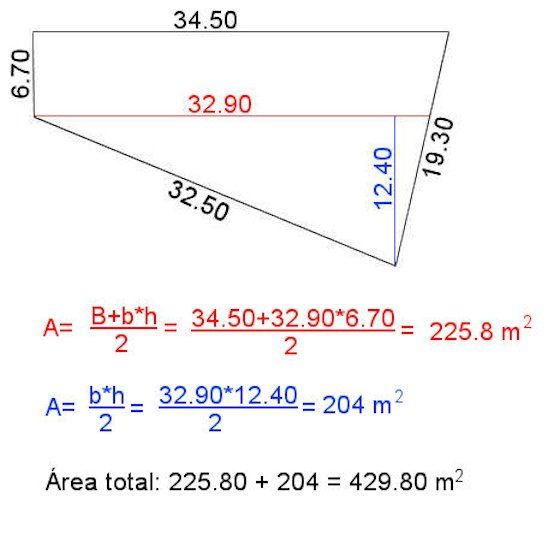
Entregar ejercicios el viernes 20
1. Hallar el área de la siguiente figura:
2.
3Queremos pintar la parte de la fachada y chimenea de la casa que se observa en la imagen. Un bote de 1 Kg de pintura cuesta 3 €, sabiendo que con 1 Kg de pintura se pintan aproximadamente 8 m² y el bote más pequeño que venden de pintura es el de 1 Kg, ¿cuánto nos costará la pintura necesaria? La basede la casa mide 10 m
4. Halla el área de un pentágono regular de 8 cm de lado y 5 cm de radio
5. Y el área de un octógono regular de 8 cm de lado y 6 cm de apotema
6. Cuál es el área de un dodecágono regular de 5 cm de lado y apotema 9.35 cm?
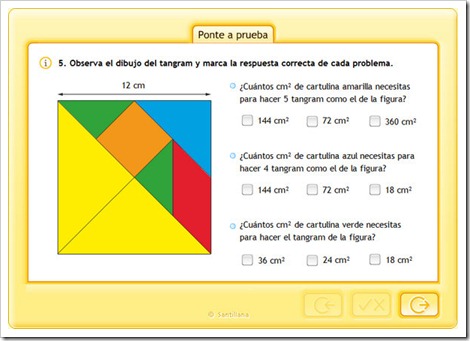
7. 
8.
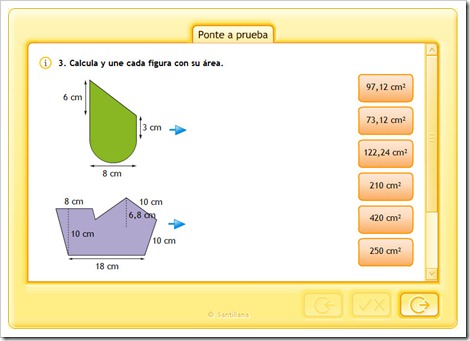
9. Cuánto vale el área de la parte subrayada de la figura, si el área del hexágono es de
cm².
10.Calcula la cantidad de pintura necesaria para pintar la fachada de este edificio sabiendo que se gastan 
kg de pintura por m².
8.
9. Cuánto vale el área de la parte subrayada de la figura, si el área del hexágono es de
cm². kg de pintura por m².
