MATE 2. SEMANA DEL 30 MARZO AL 3 ABRIL 2020
BLOQUE:
|
2
|
EJE:
|
Análisis de datos
|
TEMA:
|
Estadística
|
SECUENCIA:
|
18. Medidas de tendencia central, rango y desviación media
|
LECCIÓN:
|
1. Medidas de tendencia central
|
APRENDIZAJES ESPERADOS:
|
• Usa e interpreta las medidas de tendencia central (moda, media
aritmética y mediana), el rango y
la desviación media de un conjunto de datos y decide cuál de ellas conviene más en el análisis de los datos en cuestión. |
Te dejo este video por si te atreves a calcular las medidas de tendencia central usando excel. Si es así, también le tomas foto a la pantalla y me la mandas. No es obligatorio, es opcional.
1. Cómo calcular la media
El valor medio (también se llama la media) es simplemente el promedio de los números.
Es fácil de calcular: sólo suma los números, después divide por cuántos números hay. (En otras palabras es la suma dividida por la cuenta).
Ejemplo 1:
¿Cuál es la media de estos números?
3, 10, 5
Suma los números: 3 + 10 + 5 = 18
Divide por cuántos números hay (tenemos 3 números): 18 ÷ 3 = 6
Divide por cuántos números hay (tenemos 3 números): 18 ÷ 3 = 6
La media es 6
Ejemplo 2:
Mira estos números:
3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29
La suma de estos números es igual a 330
Hay quince números.
La media es igual a 330 ÷ 15 = 22
El valor medio de los números de arriba es 22
2. Cómo calcular la mediana
Es el número en el medio de una lista ordenada.
Para calcular la mediana, ordena los números que te han dado según su valor y encuentra el que queda en el medio.
Mira estos números:
3, 13, 7, 5, 21, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29
Si los ordenamos queda:
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56
Hay quince números. El del medio es el octavo número:
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56
La mediana de este conjunto de valores es 23.
PERO si hay una cantidad par de números la cosa cambia un poco.
En ese caso tenemos que encontrar el par central de números, y después calcular su valor medio. Esto se hace simplemente sumándolos y dividiendo entre dos.
Lo vemos mejor con un ejemplo:
En ese caso tenemos que encontrar el par central de números, y después calcular su valor medio. Esto se hace simplemente sumándolos y dividiendo entre dos.
Lo vemos mejor con un ejemplo:
3, 13, 7, 5, 21, 23, 23, 40, 23, 14, 12, 56, 23, 29
Si ordenamos los números nos queda:
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 40, 56
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 40, 56
Ahora hay catorce números así que no tenemos sólo uno en el medio, sino un par:
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 40, 56
En este ejemplo los números intermedios son 21 y 23.
Para calcular el valor en medio de ellos, sumamos y dividimos entre 2:
21 + 23 = 44
44 ÷ 2 = 22
44 ÷ 2 = 22
Así que la mediana en este ejemplo es 22.
3. Cómo calcular la moda o valor modal
La moda es simplemente el valor que aparece más veces.
Para calcular la moda tienes que ordenar los números que te dan.
Mira estos números:
3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29
Ordenados quedan:
3, 5, 7, 12, 13, 14, 20, 23, 23, 23, 23, 29, 39, 40, 56
Así es más fácil ver qué números aparecen más veces.
En este caso la moda es 23.
Cómo calcular la media aritmética en tablas de frecuencias para datos no agrupados (Ejercicio 16)
Vamos a ver ahora cómo calcular la media aritmética utilizando las tablas de frecuencias. En estos casos, tenemos un número más alto de datos no agrupados y además, estos datos pueden repetirse.
Podríamos calcular la media sumando todos los valores y dividiendo entre el número total, pero sería una operación muy larga.
En su lugar, construimos una tabla de frecuencias con los datos, donde añadiremos una columna para multiplicar cada valor por su frecuencia absoluta.
La media será la suma de cada dato por su frecuencia absoluta, dividida entre el número de datos:
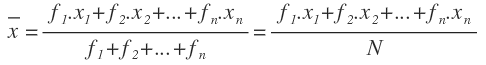
Vamos a verlo más despacio con un ejemplo.
Tenemos los siguientes datos no agrupados y nos piden calcular la media aritmética:
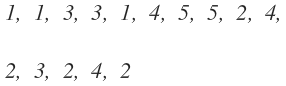
Colocamos los datos en la primer columna de la tabla de frecuencias (que explico cómo construirla en la segunda lección del curso de estadística) y su frecuencia absoluta en la segunda columna:
Ahora añadimos una tercera columna, donde iremos añadiendo la multiplicación de cada dato por su frecuencia absoluta:
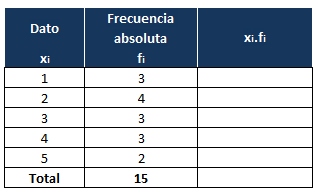
Para la primera fila sería: 1x3=3
Para la segunda fila: 2x4=8
Y así con todas las filas.
En la última fila, realizamos la suma de toda la columna:
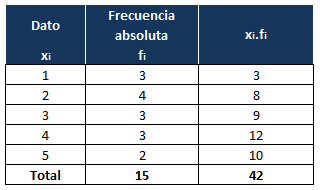
Una vez tenemos esta tabla, aplicamos la fórmula de la media aritmética:
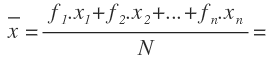
Donde el numerador es igual a la suma de cada elemento por su frecuencia, que es 42 y lo tenemos calculado en la última fila de la tercera columna y el denominador el la suma de las frecuencias absolutas, calculada en la última fila de la segunda columna y que es igual a 15:
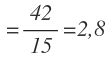
TAREA PARA ENTREGAR EL VIERNES 3 DE ABRIL A LAS 12:00 PM
1. DEBERÁN COPIARLA EN SU CUADERNO Y RESOLVERLOS. LE SACAN FOTO Y ME LA ENVÍAN
2. DEBERÁN ESTAR NUMERADOS LOS EJERCICIOS
3. DEBEN TENER PROCEDIMIENTO
4. LA FOTO DEBE ESTAR CLARA, SIN REFLEJOS O SOMBRAS.
5. ENVÍENLA COMPLETA, ES DECIR, NO EN PARTES.
6. CON LETRA Y NÚMEROS LEGIBLES, POR FAVOR!
Resolver los siguientes ejercicios
Escoge la opción que indica la mediana de cada serie de datos:
1El número de veces que come pasta durante una semana un grupo de tres amigos:
2, 5, 3
2, 5, 3
2Los litros de agua que beben al día un grupo de cuatro amigos:
2, 1, 3, 2.5
2, 1, 3, 2.5
3El número de horas que Carmen ha visto la tele durante cada día de la semana pasada es:
3, 2, 3, 3, 2, 6, 3
3, 2, 3, 3, 2, 6, 3
4Las veces que se cepilla María los dientes al día durante dos semanas:
1, 1, 2, 2, 3, 3, 3, 3, 4, 4, 2, 2, 5, 1.
1, 1, 2, 2, 3, 3, 3, 3, 4, 4, 2, 2, 5, 1.
5Las notas de los exámenes de matemáticas realizados durante el curso por Pablo son:
7, 5, 6, 8, 7, 8, 8, 9, 10, 10.
7, 5, 6, 8, 7, 8, 8, 9, 10, 10.
6El número de horas que dedican los veintitres alumnos de una clase a realizar un trabajo de investigación de Geometría:
5, 10, 10, 11, 12, 12, 12, 13, 14, 15, 14, 15, 15, 15, 14, 15, 17, 18, 18, 20, 20, 13, 23
5, 10, 10, 11, 12, 12, 12, 13, 14, 15, 14, 15, 15, 15, 14, 15, 17, 18, 18, 20, 20, 13, 23
7Las estaturas en centímetros de un grupo de dieciseis amigos:
150, 160, 164, 157, 183, 163, 182, 170, 159, 157, 151, 161, 163, 178, 173, 172.
150, 160, 164, 157, 183, 163, 182, 170, 159, 157, 151, 161, 163, 178, 173, 172.
8El número de veces que va al cine en un mes cada componente de un grupo de once amigos es:
2, 0, 2, 3, 1, 1, 2, 3, 1, 1, 3
2, 0, 2, 3, 1, 1, 2, 3, 1, 1, 3
Contesta a las siguientes cuestiones:
9Las notas de matemáticas de los 26 alumnos de una clase son:
6, 2, 4, 4, 5, 5, 6, 3, 8, 6, 5, 3, 7, 6, 5, 6, 4, 4, 4, 3, 5, 5, 4, 6, 7, 4
Calcula la mediana:
Me =
10Las faltas de asistencia de 25 alumnos de otra clase son:
0, 1, 1, 1, 3, 2, 2, 7, 1, 2, 1, 0, 0, 0, 1, 2, 1, 2, 1, 2, 0, 0, 4, 6, 7
Calcula la mediana:
Me =
11. Encontrar
la media, mediana y moda de los siguientes valores: 84; 91; 72; 68; 87;
78; 65; 87; 79.
Calcula lo que se te pide, no calcules el rango
12 Se le pregunta a un grupo de personas acerca de la cantidad de libros que leyó durante el año 2015, y las respuestas son: 4; 3; 2; 7; 10; 8; 2; 9; 3; 6; 8; 1; 1; 9; 2. La moda de la muestra es:
a) 2 b) 3 c) 4 d) 5 e) 9
13 Halla la mediana de las siguientes series estadísticas.
a) 1, 7, 3, 2, 4, 6, 2, 5, 6
b) 4, 2, 1, 3, 8, 5, 3, 1, 6, 7
14 Se tienen dos distribuciones cuyos datos son los siguientes:
Distribución A: 9, 5, 3, 2, 1, 2, 6, 4, 9, 8, 1, 3, 5, 4, 2, 6, 3, 2, 5, 6, 7
Distribución B: 1, 1, 3, 2, 5, 6, 7, 2, 5, 4, 3, 1, 2, 1, 5, 7, 8, 9, 9, 2, 1
a) Halla la moda de ambas distribuciones
15 Se tiene el siguiente conjunto de datos:
10, 13, 4, 7, 8, 11, 10, 16, 18, 12, 3, 6, 9, 9, 4, 13, 20, 7, 5, 10, 17, 10, 16, 14, 8, 18
a) Obtén la mediana
16.Calcular la media de la siguiente distribución:
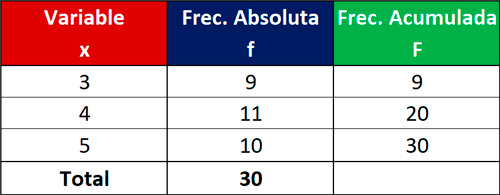. Las puntuaciones obtenidas por un grupo en una prueba han sido: (Los puedes hacer con excel).
CAlcular la media, moda y mediana
17.
18. El número de estrellas de los hoteles de una ciudad viene dado por la siguiente serie:
