MATE 3. SEMANA DEL 30 MARZO AL 3 ABRIL 2020

Bloque:	3
Eje:	Número, álgebra y variación
TEMA:	Patrones, figuras geométricas y expresiones equivalentes
APRENDIZAJES ESPERADOS:	• Resuelve y plantea problemas que involucran ecuaciones lineales, sistemas de ecuaciones y ecuaciones de segundo grado.

Sistema de ecuaciones | Teoría y ejercicios

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas en la que deseamos encontrar una solución común.

En esta ocasión vamos a resolver un sistema de dos ecuaciones lineales con dos incógnitas.

Una ecuación lineal con dos incógnitas es una igualdad del tipo ax+by=c, donde a, b, y c son números, y «x» e «y» son las incógnitas.

Una solución es todo par de números que cumple la ecuación.

Los sistemas de ecuaciones lineales los podemos clasificar según su número de soluciones:

• Compatible determinado: Tiene una única solución, la representación son dos rectas que se cortan en un punto.
• Compatible indeterminado: Tiene infinitas soluciones, la representación son dos rectas que coinciden.
• Incompatible: No tiene solución, la representación son dos rectas paralelas.

 Existen diferentes métodos de resolución:

• Sustitución.
•  Reducción.
•  Igualación.

En esta ocasión vamos a resolver un sistema de dos ecuaciones lineales con dos incógnitas. Por ejemplo:

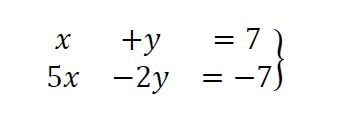
Sistema de ecuaciones: método de sustitución

A través del método de sustitución lo que debemos hacer es despejar una de las incógnitas en una de las ecuaciones y sustituir su valor en la siguiente. Lo veremos con más detalle en el siguiente ejemplo:

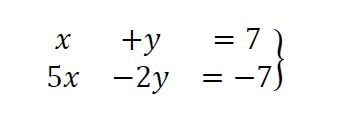
Lo primero que hacemos es despejamos una de las incógnitas en la primera ecuación.

x+y=7
x= 7-y

Posteriormente, sustituimos en la segunda ecuación el valor correspondiente de la «x».

5x-2y         =  -7
5(7-y) -2y  =  -7

Ahora, despejamos la «y».

35-5y-2y =  -7
35-7y     =  -7
      -7y        =  -7-35
-7y           =  -42
                      y       =  -42/-7      =6

y=6

Por último, utilizamos el valor de «y» para hallar el valor de «x», es decir, susutituimos el valor de  y en t

x = 7-y

    x   = 7-6  =1

x=1

La solución de nuestro sistema es x=1 e y =6.

Sistema de ecuaciones: método de reducción

Con el método de reducción lo que hacemos es combinar, sumando o restando, nuestras ecuaciones para que desaparezca una de nuestras incógnitas.

Los pasos a seguir son los siguientes:

En primer lugar, necesitamos preparar las dos ecuaciones, si es necesario, multiplicándolas por los números que convenga.

En este caso, queremos reducir la «y» de nuestro sistema, por tanto, multiplicamos la primera ecuación por 2.

2(x+y=7)
5x-2y=-7

Así, el sistema se queda:

Con esto igualamos los coeficientes de las  y  (+2 y -2) y mira lo que pasa.

Si nos fijamos, sumando las ecuaciones la y nos desaparece.

Y nos quedaría:

7x  =7
          x   =7/7  =1
x=1

Por último, sustituimos el valor que hemos calculado despejando la otra incógnita en una de las ecuaciones iniciales.

y= 7-x

    y =7-1  =6

y  =6

La solución de nuestro sistema es x=1 e y =6.

TAREA PARA ENTREGAR EL VIERNES 3 DE ABRIL A 

LAS               12:00 PM

1. DEBERÁN COPIARLA  EN SU CUADERNO Y RESOLVERLOS. LE SACAN FOTO Y ME LA ENVÍAN

2. DEBERÁN ESTAR NUMERADOS LOS EJERCICIOS

3. DEBEN TENER PROCEDIMIENTO

4. LA FOTO DEBE ESTAR CLARA, SIN REFLEJOS O SOMBRAS.

5. ENVÍENLA COMPLETA, ES DECIR, NO EN PARTES.

6. CON LETRA Y NÚMEROS LEGIBLES, POR FAVOR!

1.

$\begin{array}{l}2x=3y-1\\ 6x-9y=-3\end{array}$

¿Cuántas soluciones tiene el sistema?

Escoge 1 respuesta:

Escoge 1 respuesta:

• 
  

  
  

  
  

  Exactamente una solución
• 
  

  
  

  
  

  Ninguna solución
• 
  

  
  

  
  

  Una infinidad de soluciones

. 

2.

​y=3x+812x−4y=−32​

¿Cuántas soluciones tiene el sistema?

Problema 3

Dos números suman 25 y el doble de uno de ellos es 14. ¿Qué números son?

Problema 4

El doble de la suma de dos números es 32 y su diferencia es 0. ¿Qué números son?

Problema 5

La suma de dos números es 12 y la mitad de uno de ellos el doble del otro. ¿Qué números son?

Problema 6

Ana tiene el triple de edad que su hijo Jaime. Dentro de 15 años, la edad de Ana será el doble que la de su hijo. ¿Cuántos años más que Jaime tiene su madre?

7. Averiguar el número de animales de una granja sabiendo que:

• la suma de patos y vacas es 132 y la de sus patas es 402.
• AYUDA? No puedes? Te ayudo un poco

p = número de patos

v = número de vacas

La suma de los animales es 132: Haz una ecuación aquí

La suma de las patas es 402 (dos patas por pato y cuatro por vaca):Haz la otra ecuación aquí

8. Tenemos dos números cuya suma es 0 y si a uno de ellos le sumamos 123 obtenemos el doble del otro. ¿Qué números son?

Resolver los siguiente sistemas por los dos métodos

9. 

10. Encontrar la solución del sistema de ecuaciones lineales dado por:

por cualquier método.

11-14. Resolver los siguientes sistemas de ecuaciones por el

método de reducción