MATE 3. Semana del 10 al 14 septiembre 2018

septiembre 09, 2018

EJE: Forma, espacio y medida.
TEMA: Figuras y cuerpos geométricos
Aprendizaje esperado: Construye polígonos semejantes. Determina y usa criterios de semejanza de triángulos.

Explicitación de los criterios de congruencia y semejanza de triángulos a partir de construcciones con información determinada.

Criterios de semejanza de triángulos

Para comprobar si dos triángulos son semejantes no hace falta comprobar que los lados son proporcionales y los ángulos iguales, basta con comprobar que cumplen alguno de estos tres criterios.

Primer criterio: Criterio AA (ángulo - ángulo)

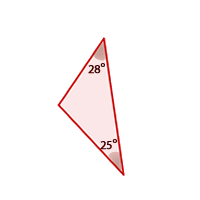
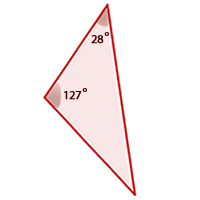
Dos triángulos que tienen dos ángulos iguales son semejantes.

Actividad 1

En el siguiente applet aparecen dos triángulos con dos ángulos iguales.

Puedes hacer variar el valor de los ángulos utilizando los deslizadores.

Puedes hacer variar el lado c moviendo los vértices A o B.

Comprueba, arrastrando uno de ellos sobre el otro, que los dos triángulos se pueden colocar en posición de Thales en todos los casos.

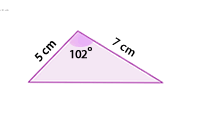
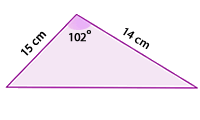
Segundo criterio: Criterio LAL (lado - ángulo - lado)

Dos triángulos que tienen un ángulo igual comprendido entre lados proporcionales, son semejantes.

Actividad 2

En el siguiente applet aparecen dos triángulos con un ángulo igual y los lados que lo forman proporcionales.

Puedes hacer variar la amplitud del ángulo utilizando el deslizador verde y la constante de proporcionalidad entre los lados, con el deslizador gris.

También puedes modificar el tamaño del triángulo azul moviendo cualquiera de sus vértices.

Comprueba que, en cualquier caso, los triángulos se pueden colocar en posición de Thales.

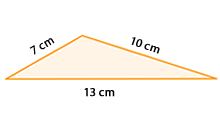
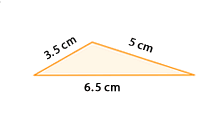
Tercer criterio: Criterio LLL (lado - lado - lado)

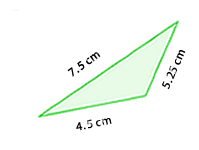
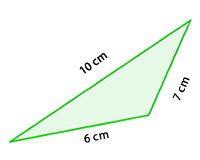
Dos triángulos que tienen los tres lados proporcionales son semejantes.

Actividad 3

En el siguiente applet aparecen dos triángulos con los tres lados proporcionales.

Puedes hacer variar la constante de proporcionalidad utilizando el deslizador.

También puedes mover los vértices del triángulo ABC para cambiar la forma.

Comprueba, que en cualquier caso, los dos triángulos siempre se pueden colocar en posición de Thales.

1 Dos triángulos son semejantes si tienen dos ángulos iguales.

2 Dos triángulos son semejantes si tienen los lados proporcionales.

3 Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.

TAREA PARA ENTREGAR EL JUEVES 13

1 Calcular la altura de un edificio que proyecta una sombra de 6.5 m a la misma hora que un poste de 4.5 m de altura da una sombra de 0.90 m.

2 Los catetos de un triángulo rectángulo que miden 24 m y 10 m. ¿Cuánto medirán los catetos de un triángulo semejante al primero cuya hipotenusa mide 52 m?