MATE 2. Semana del 10 al 14 septiembre 2018
Cálculo de productos y cocientes de potencias enteras positivas de la misma base y potencias de una potencia. Significado de elevar un número natural a una potencia de exponente negativo.
Los exponentes también se llaman potencias o índices.
6 · 6 · 6 · 6 · 6 = 65
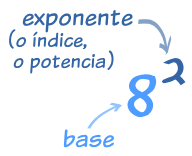
Base de una potencia
La base de una potencia es el número que multiplicamos por sí mismo, en este caso el 6.
Exponente de una potencia
El exponente de una potencia indica el número de veces que multiplicamos labase, en el ejemplo es el 5.
¿Qué pasa si el exponente es 1 o 0?
- Si el exponente es 1, entonces tienes el número solo (por ejemplo 91 = 9)
- Si el exponente es 0, la respuesta es 1 (por ejemplo 90 = 1)
Cualquier número elevado a cero, el resultado es 1.
Ya sabes que el cociente de dos números iguales es 1: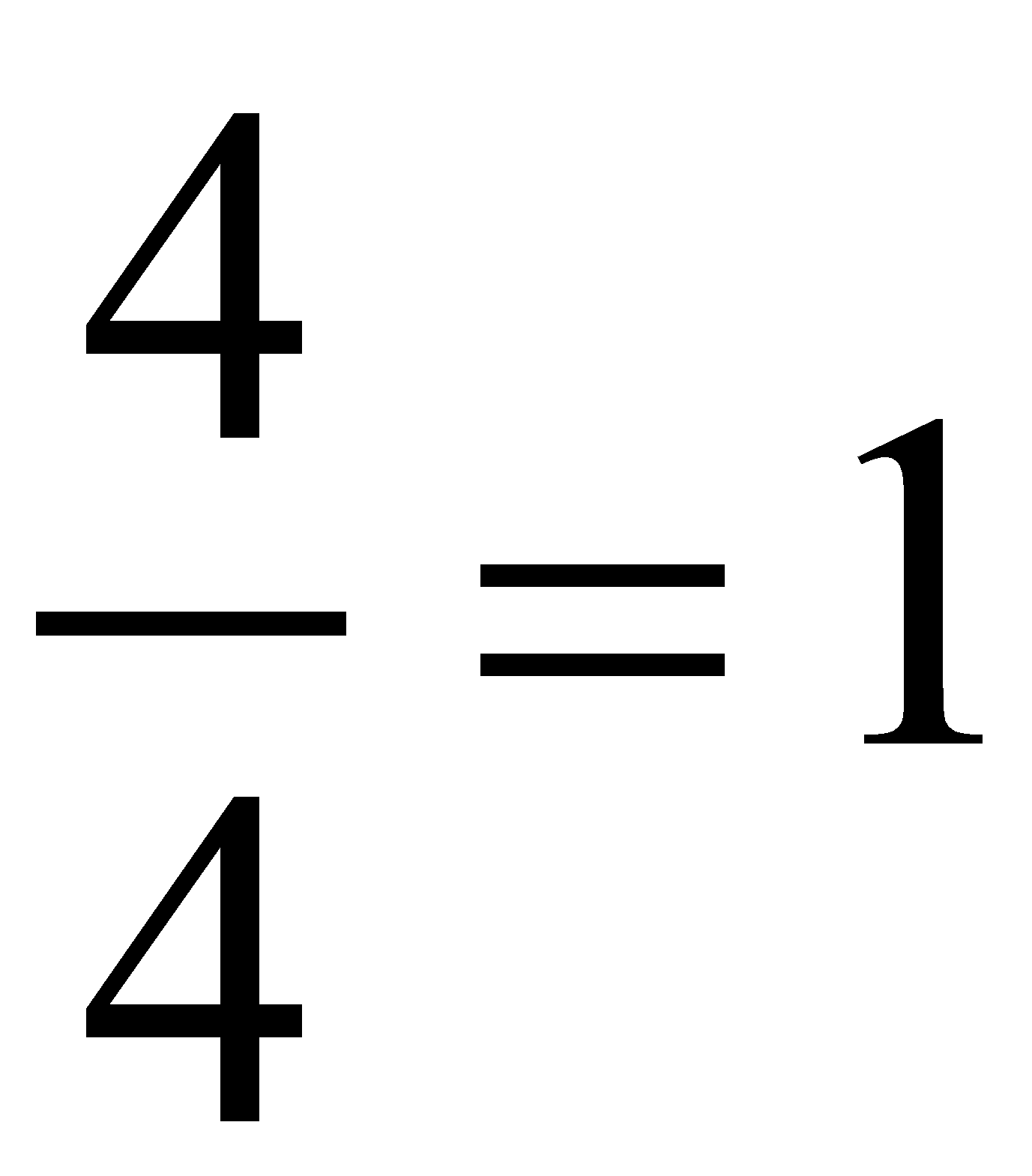 
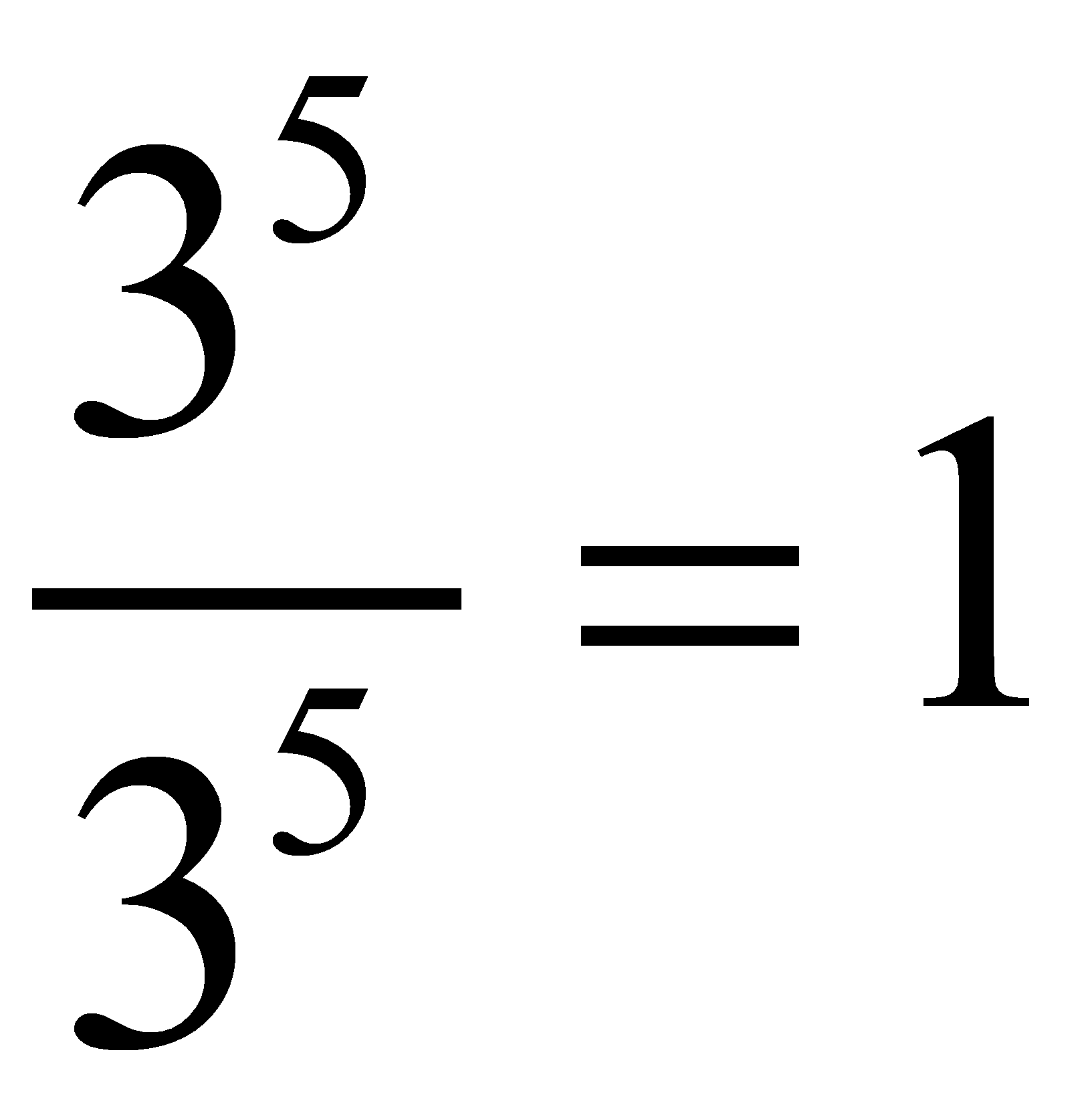Pero también 
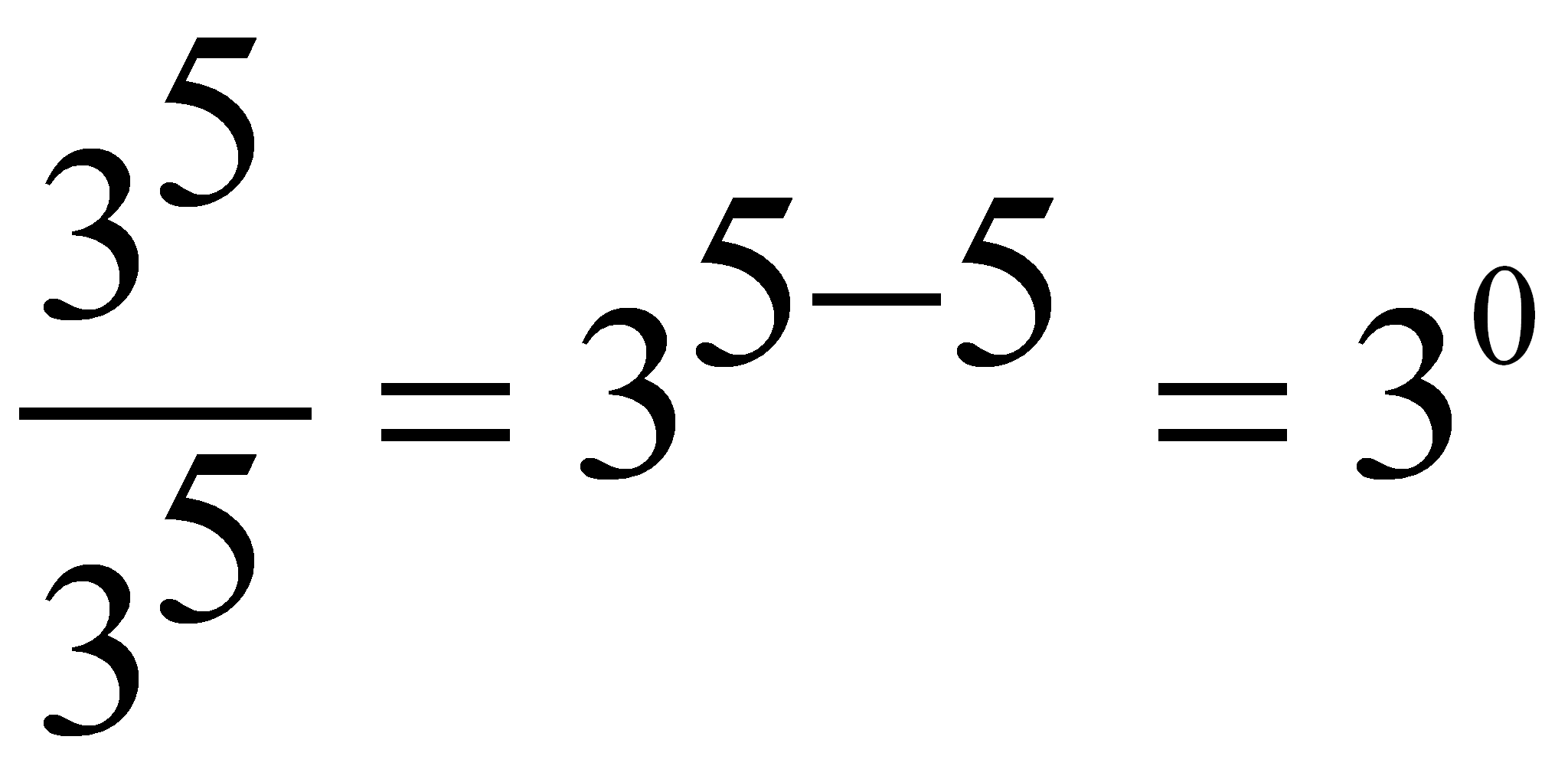Luego 
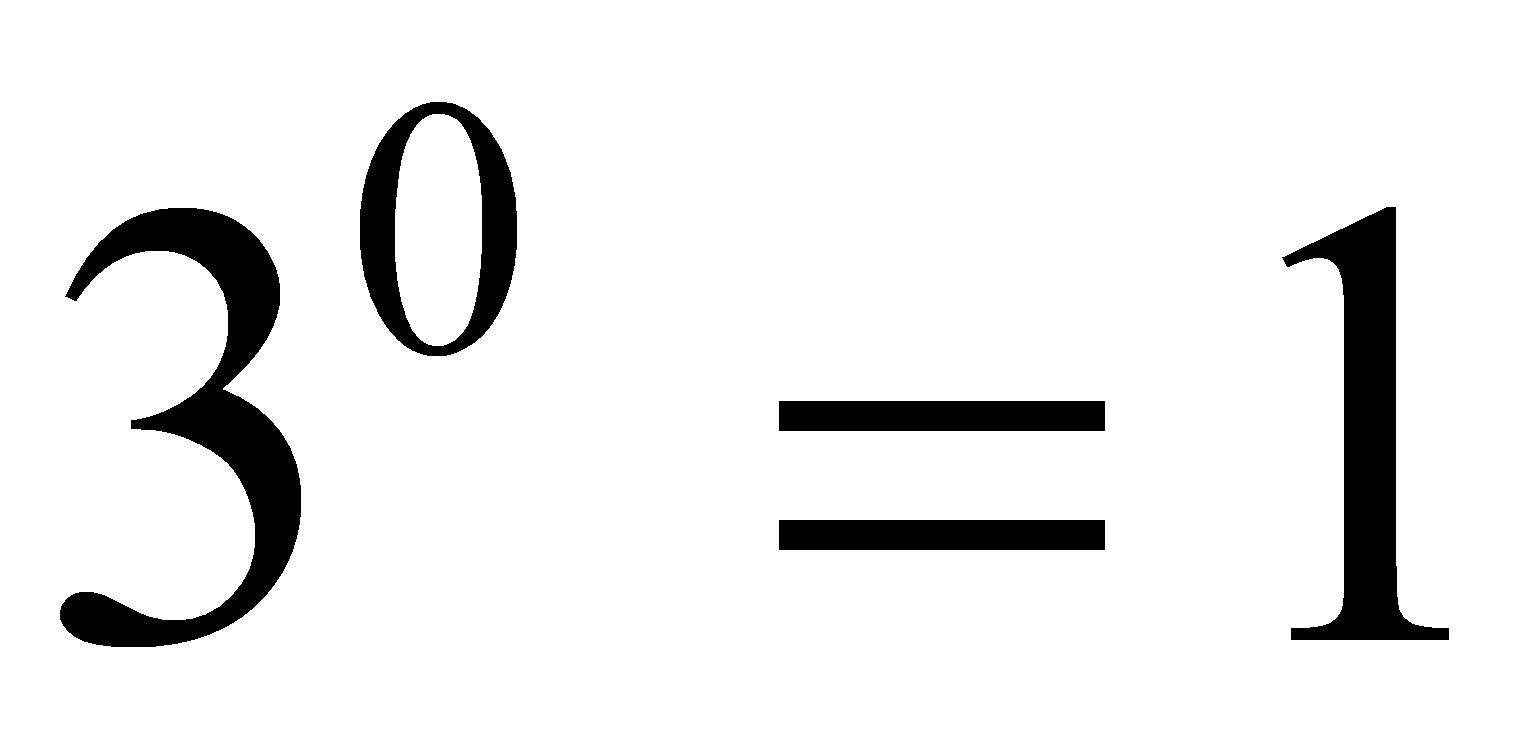En el caso: 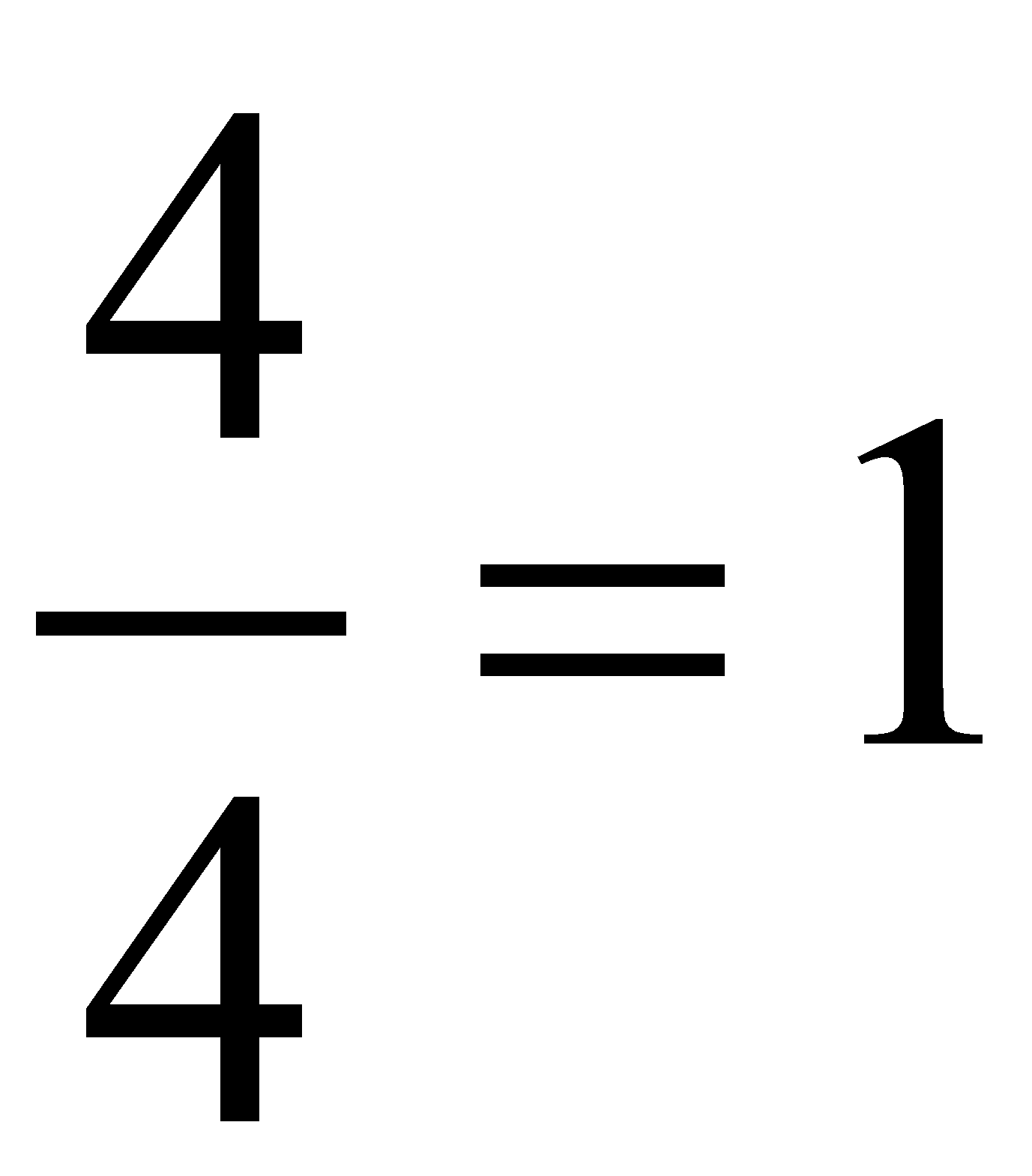Podemos decir: 
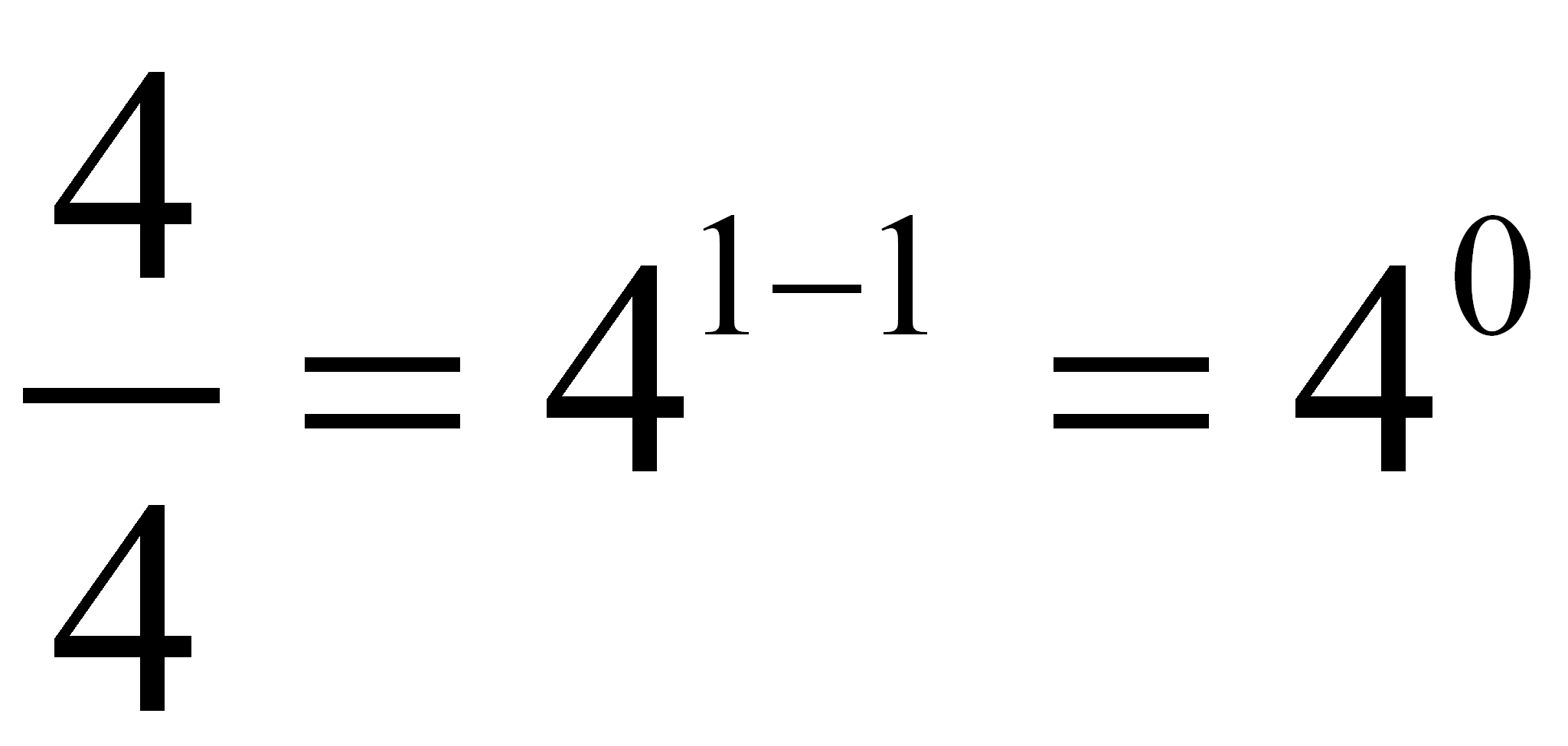Luego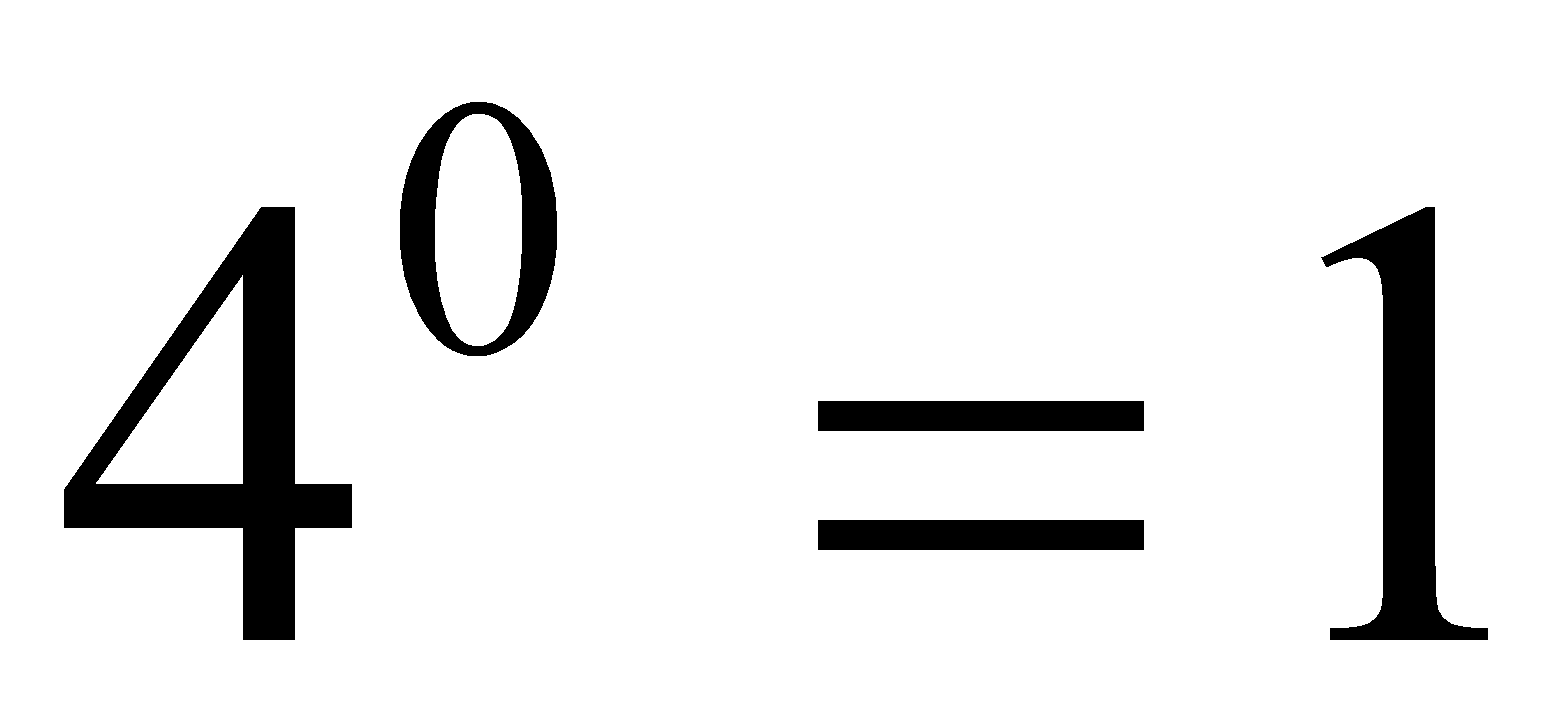 
Productos de potencias:
Si tenemos que multiplicar dos potencias que tienen la misma base te basta escribir la misma base y como exponente escribes la suma de los exponentes:
= 
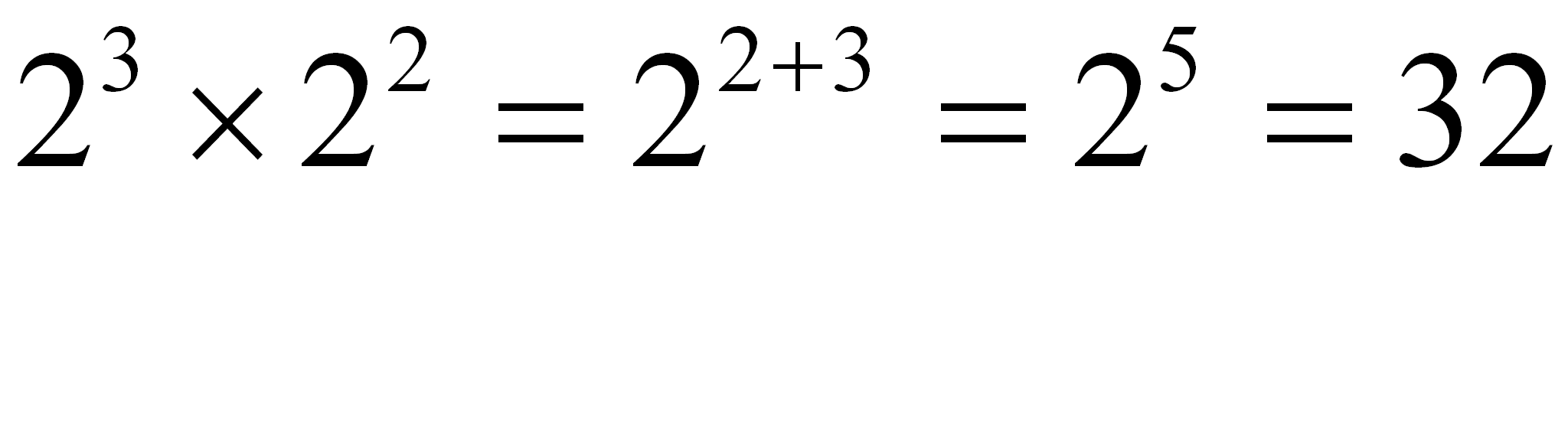
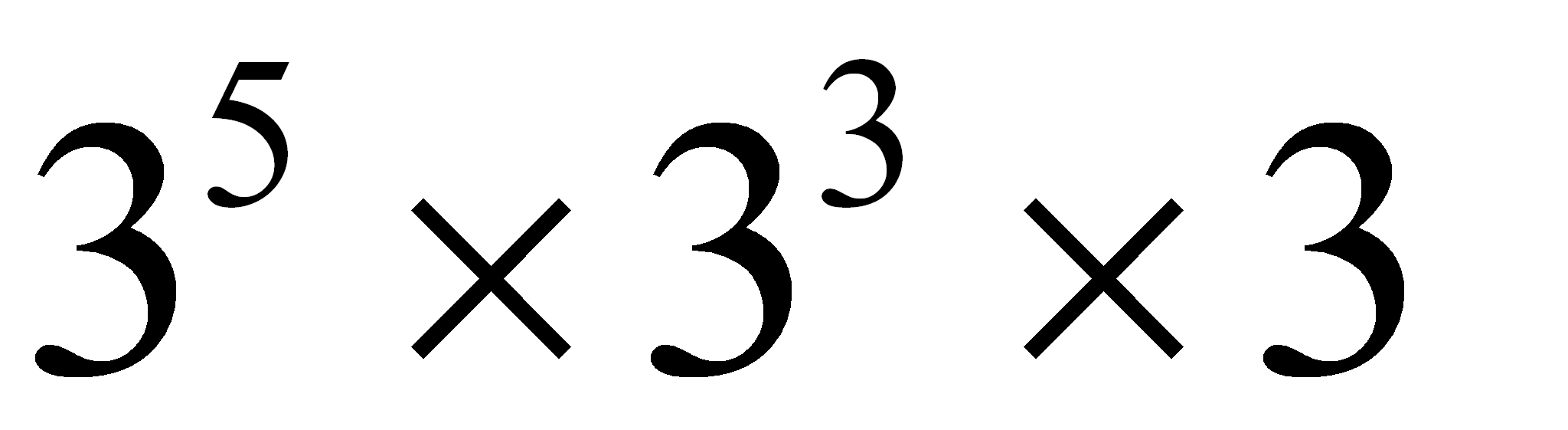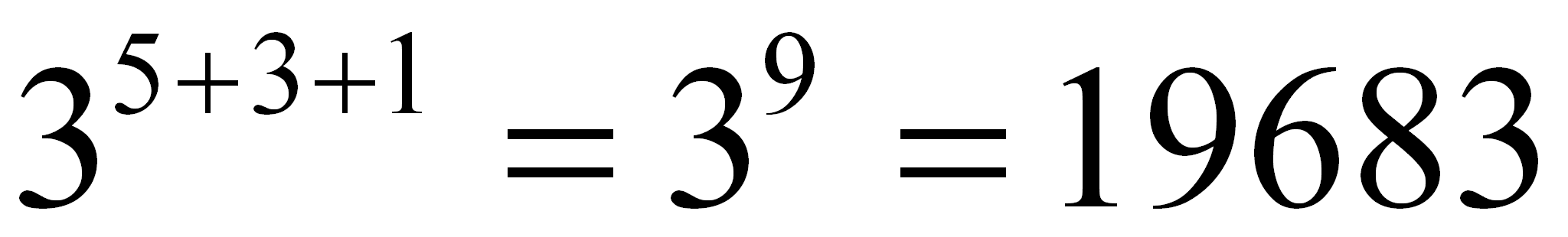
Los exponentes hacen más fácil escribir muchas multiplicaciones
**** Si las bases no son iguales NO SE DEBEN SUMAR LOS EXPONENTES. Primero calculas una potencia y después la segunda, luego la siguiente si es
que existe, y al final, multiplicas los resultados que has obtenido***
Ejemplo 1: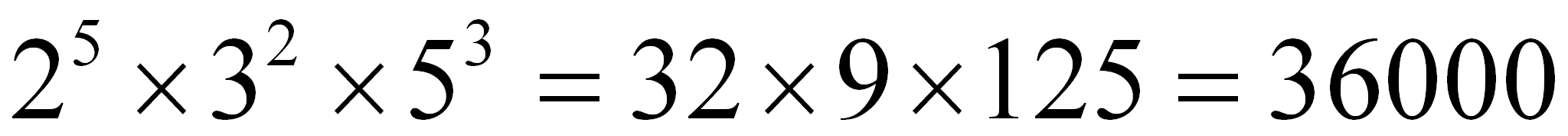 
Ejemplo 2: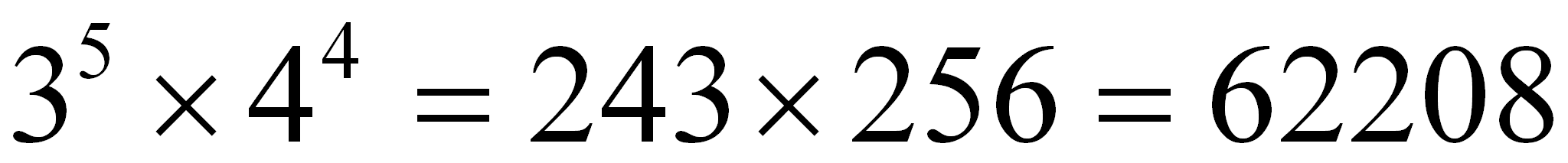 
Ya sabes que el cociente de dos números iguales es 1: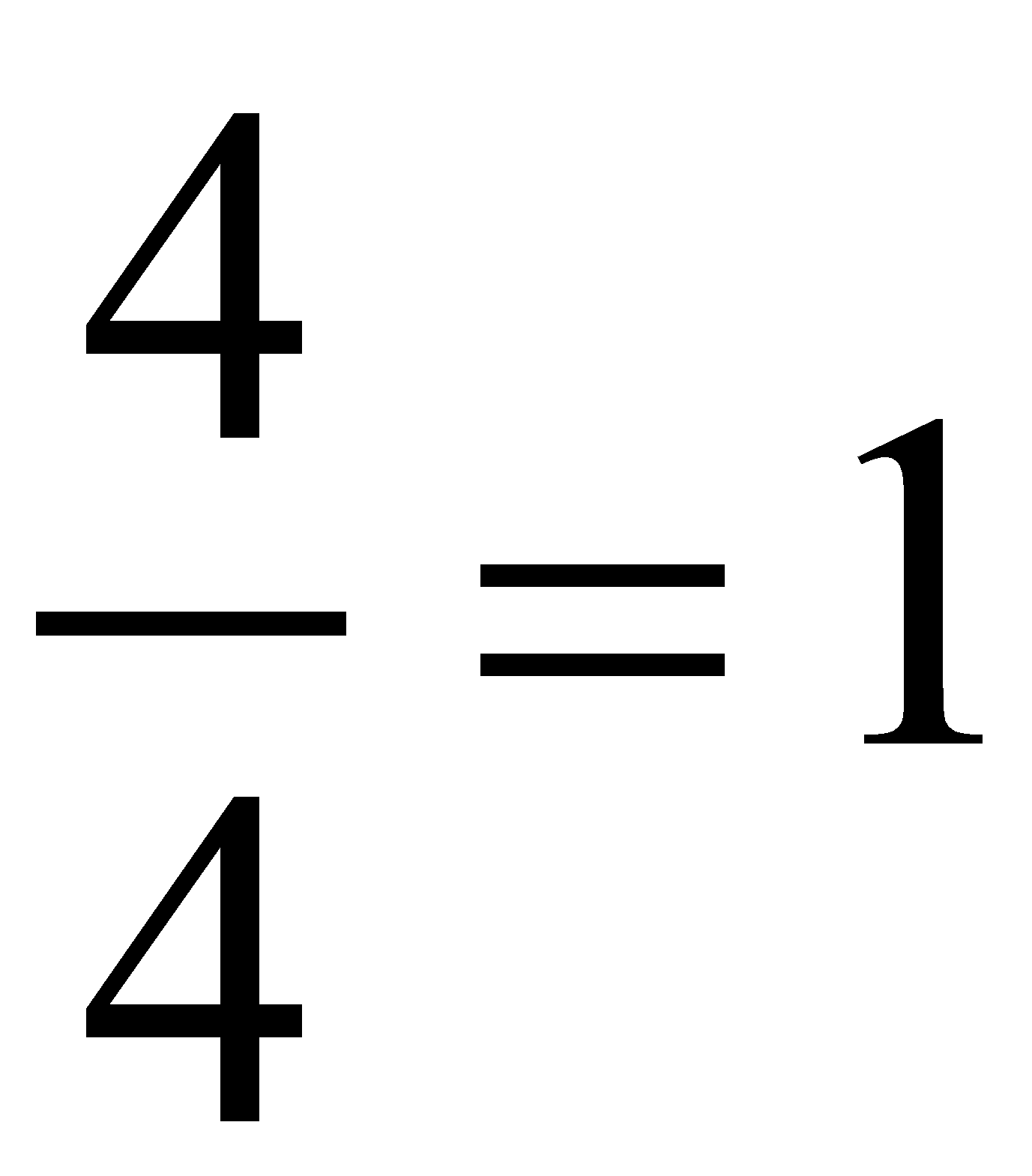
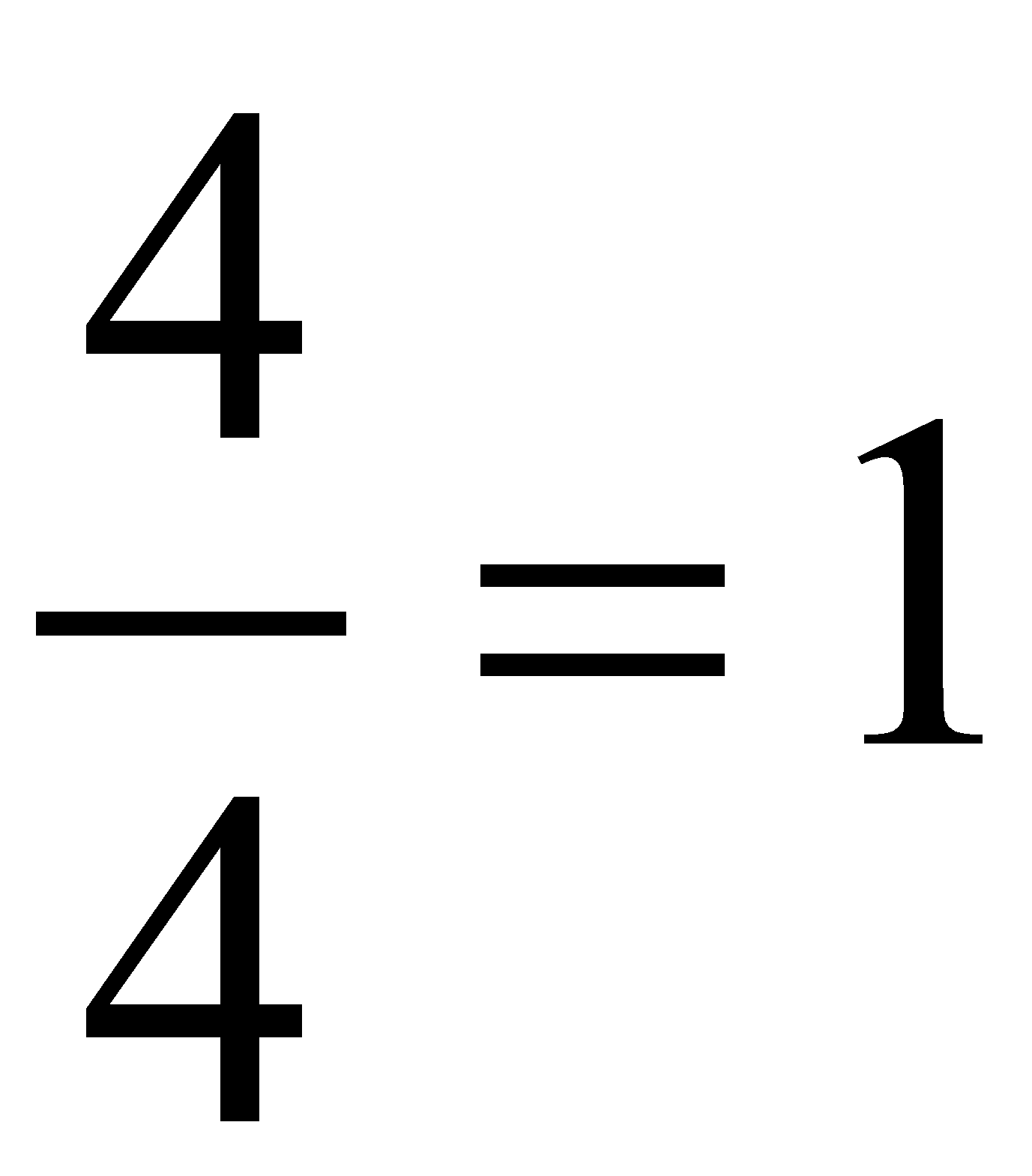
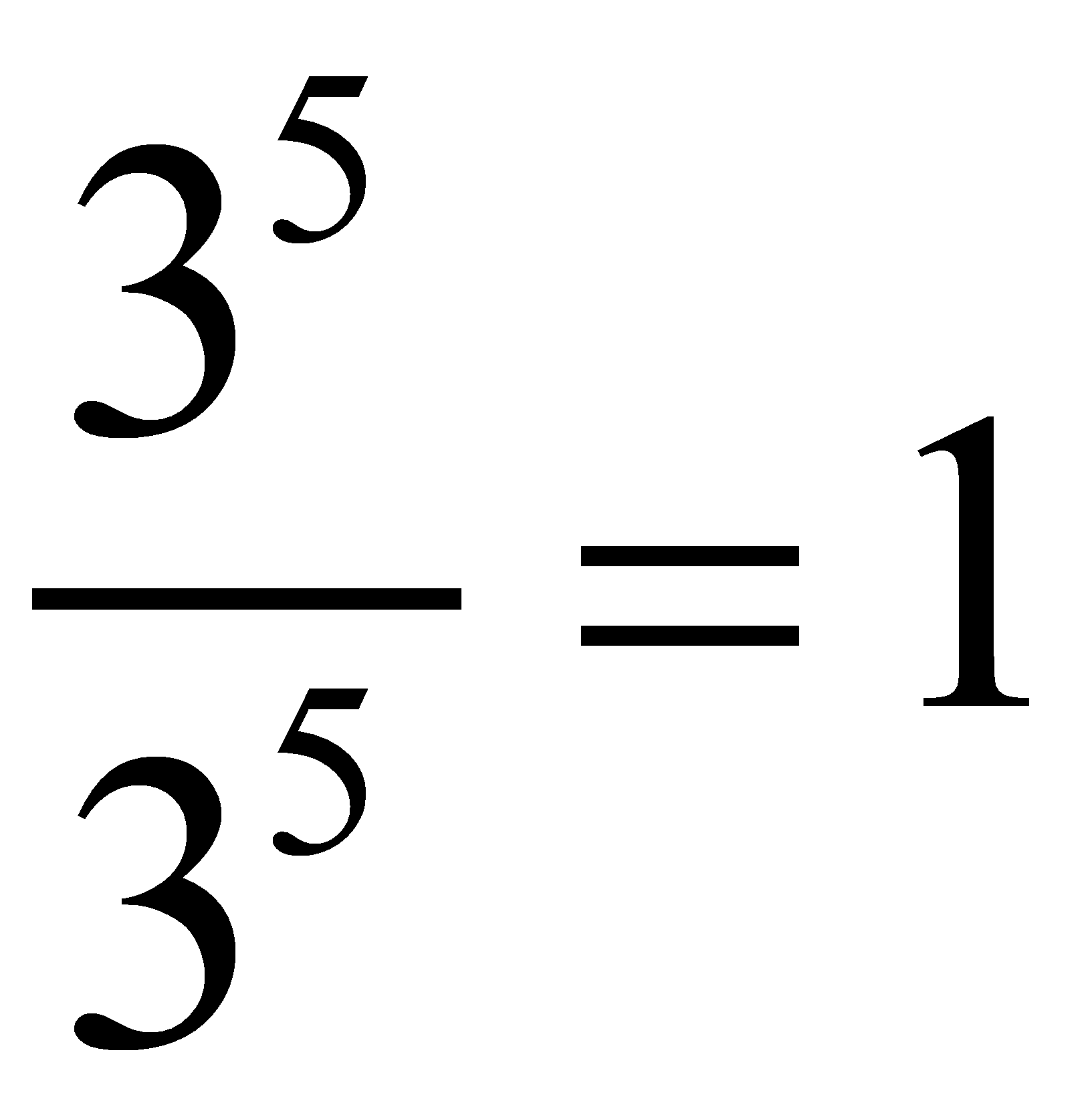Pero también 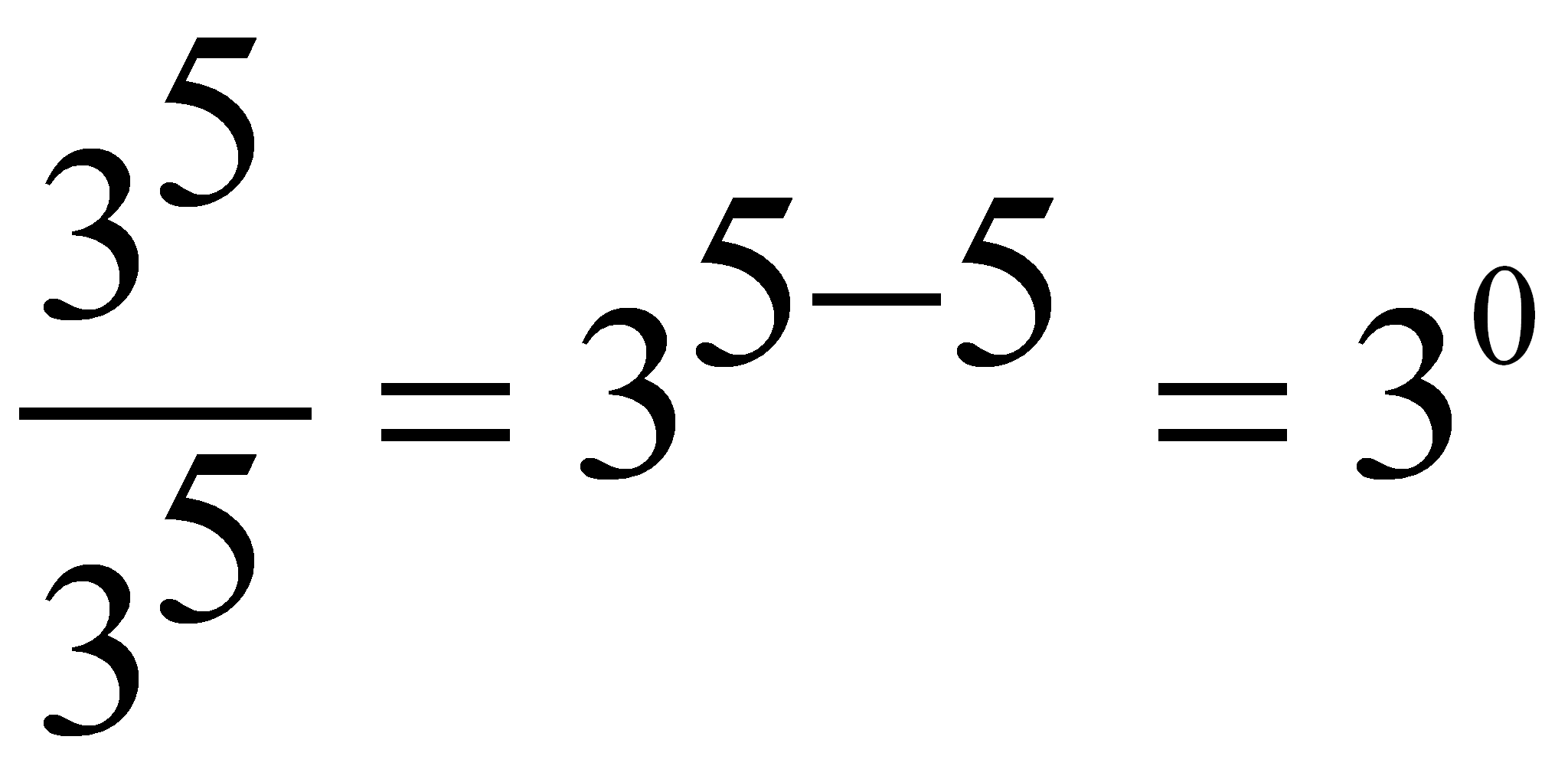Luego
En el caso: 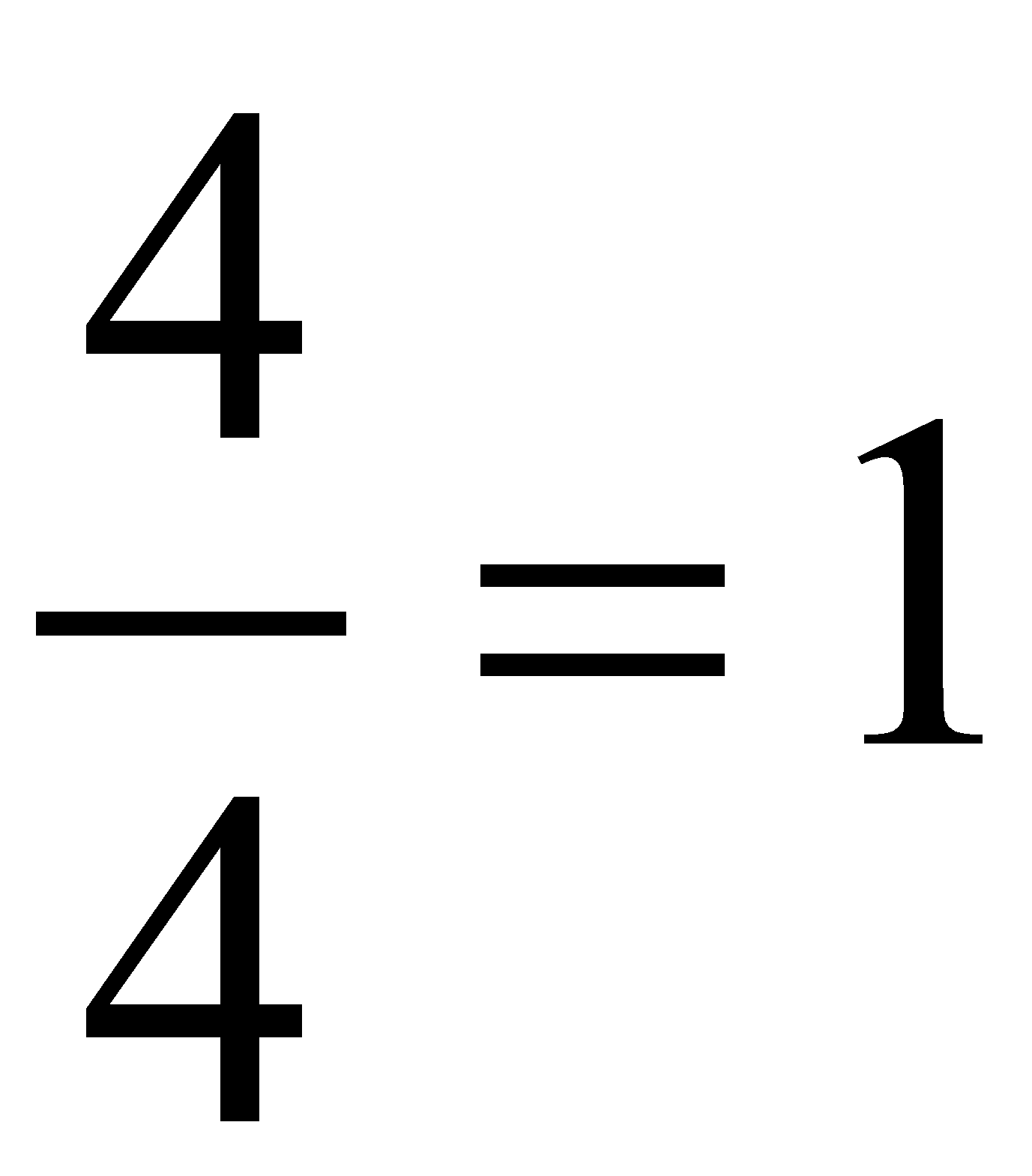Podemos decir: 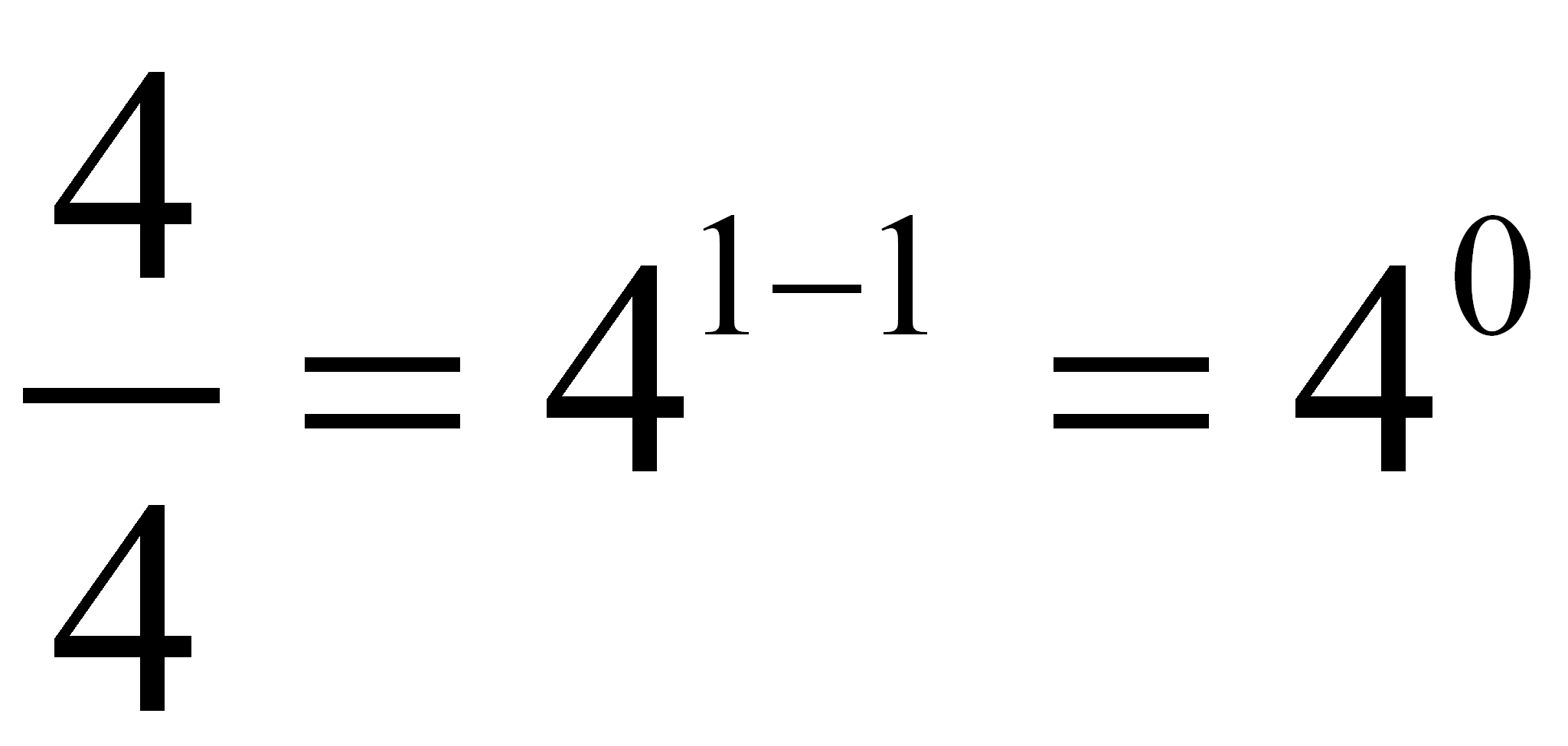Luego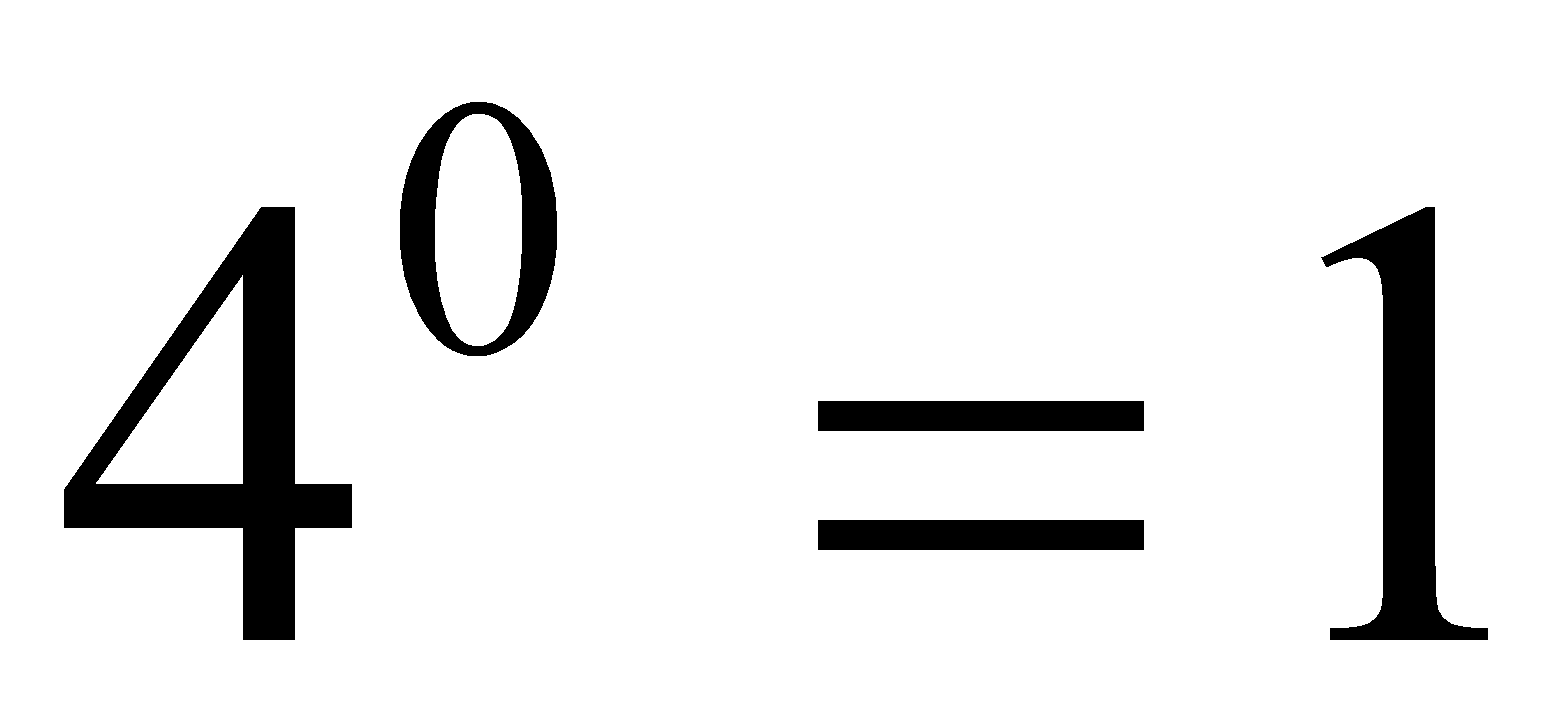
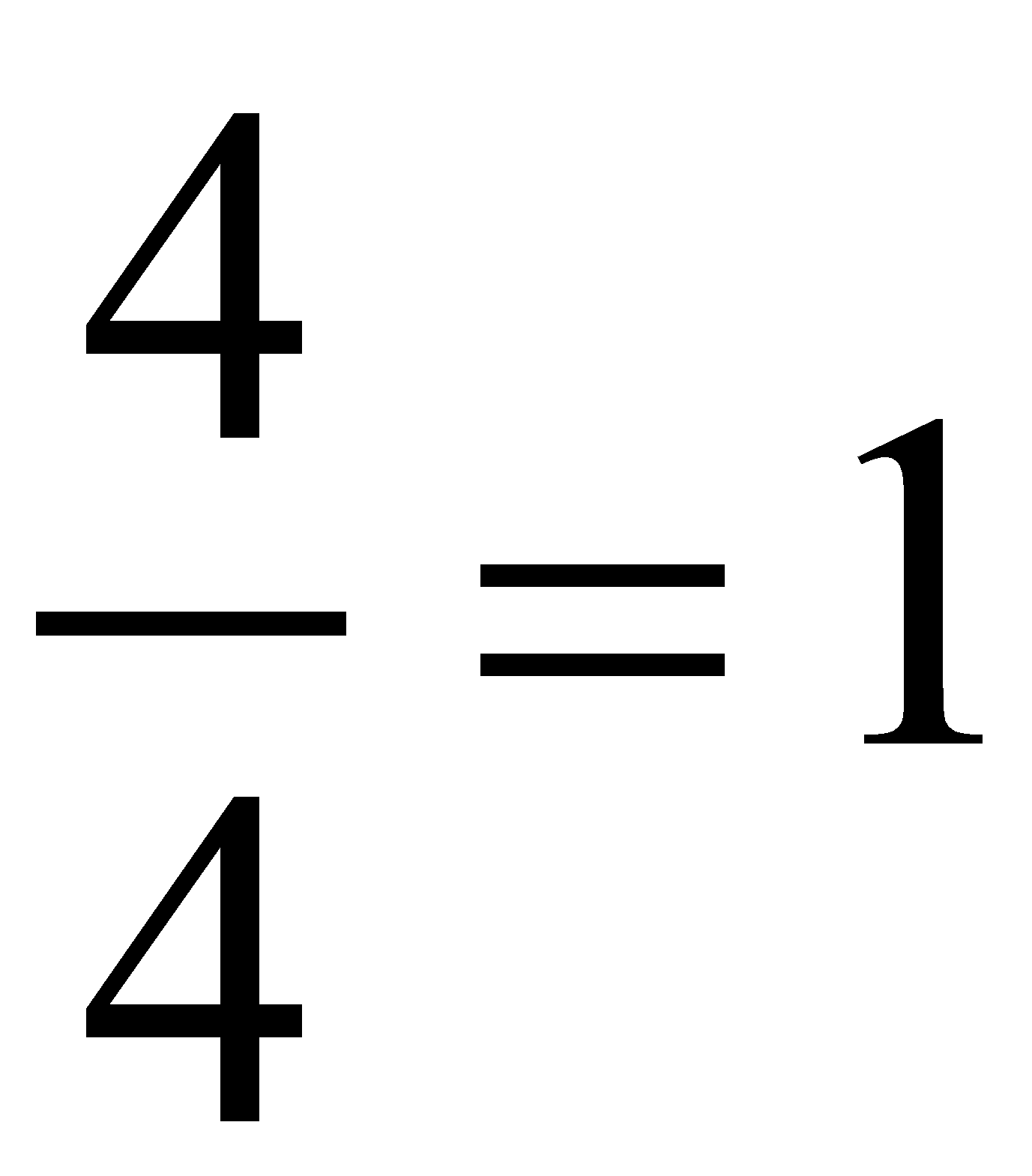Podemos decir: 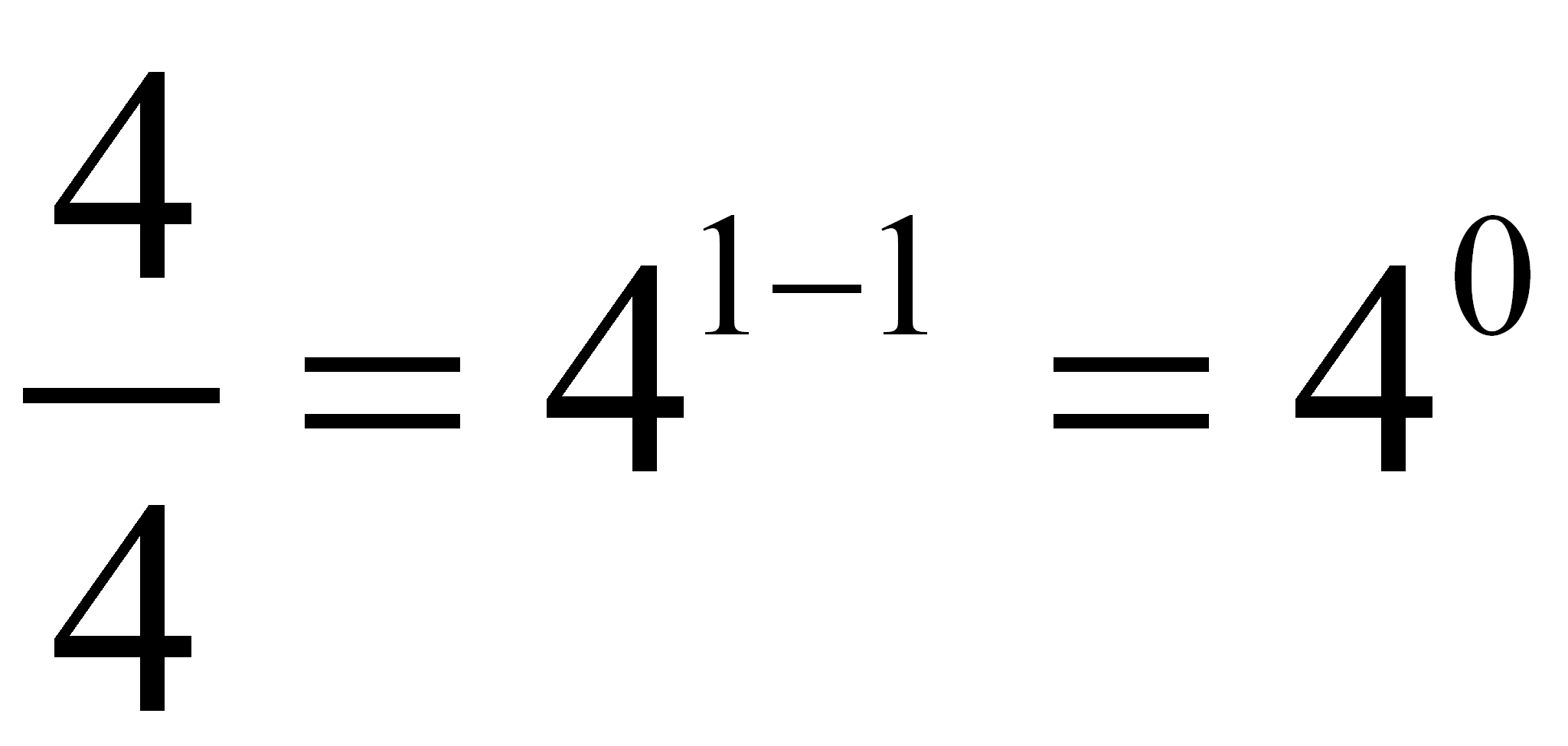Luego Productos de potencias:
Si tenemos que multiplicar dos potencias que tienen la misma base te basta escribir la misma base y como exponente escribes la suma de los exponentes:
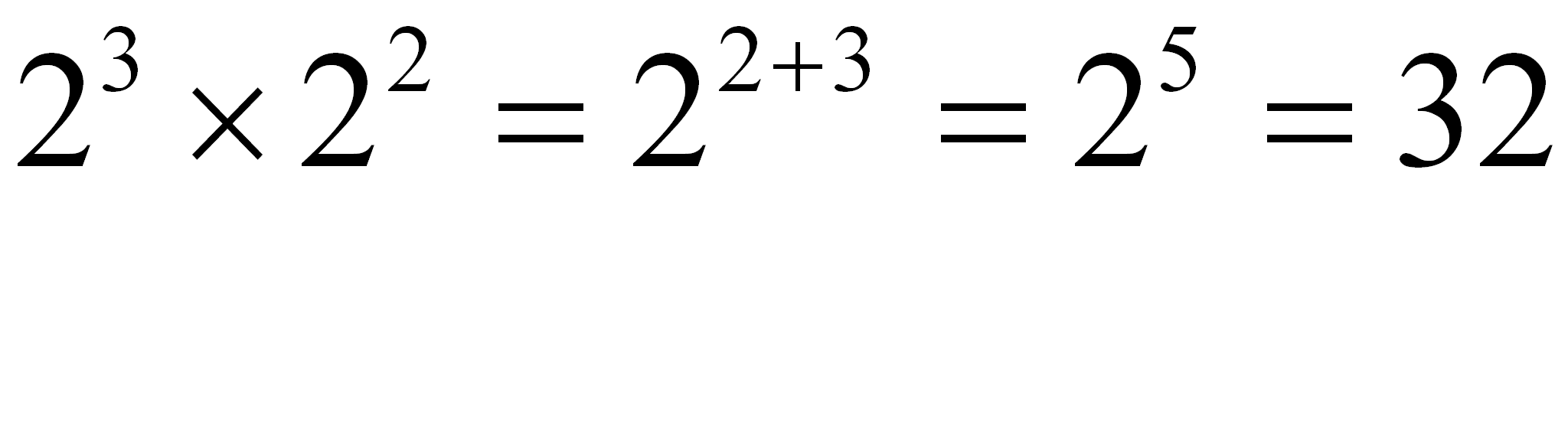
= **** Si las bases no son iguales NO SE DEBEN SUMAR LOS EXPONENTES. Primero calculas una potencia y después la segunda, luego la siguiente si es
que existe, y al final, multiplicas los resultados que has obtenido***
Ejemplo 1:
Ejemplo 2:
MULTIPLICAR POTENCIAS CON EL MISMO EXPONENTE:
Si los exponentes son iguales, puedes multiplicar las bases y colocar el mismo exponente:
DIVIDIR POTENCIAS DE LA MISMA BASE:
Para dividir potencias que tengan la misma base, se restan los exponentes. Recuerda, para multiplicar se suman los exponentes, para dividir, se restan:
ejemplo 1.-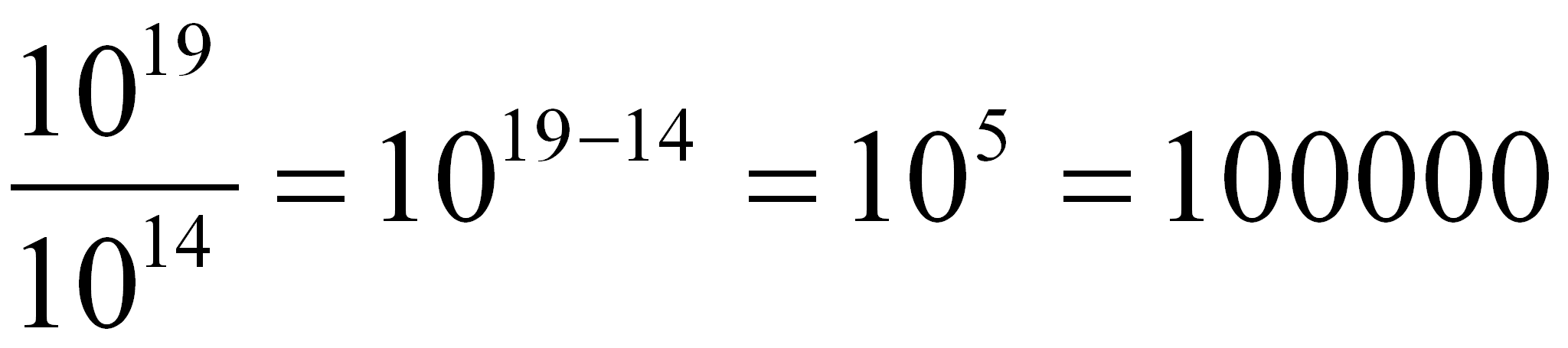 
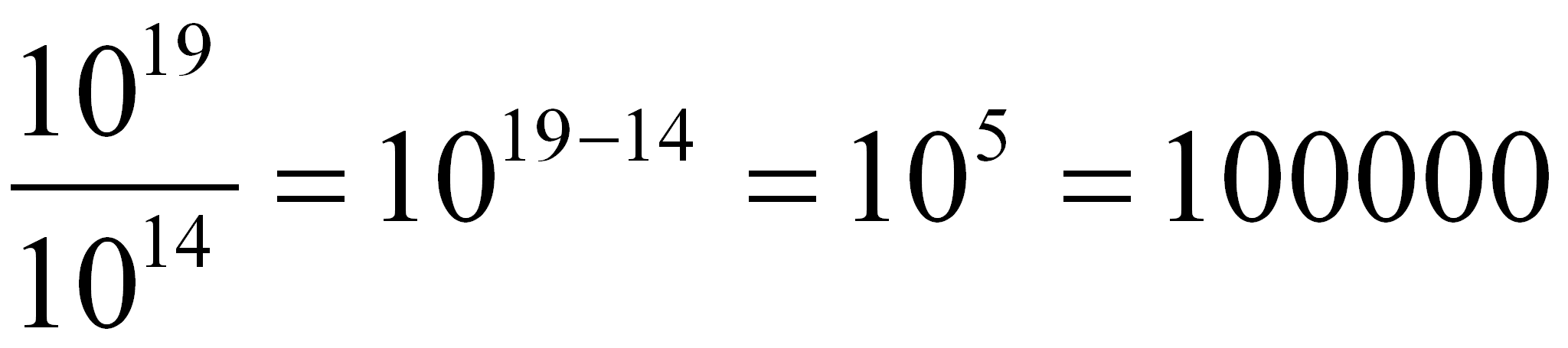
ejemplo 2.-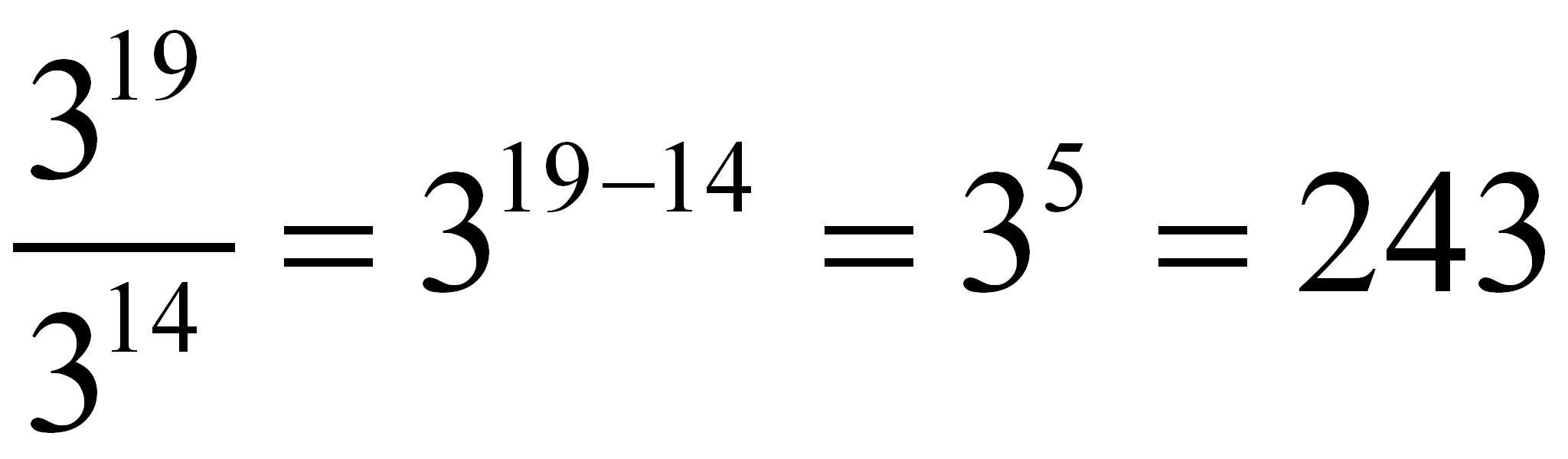 
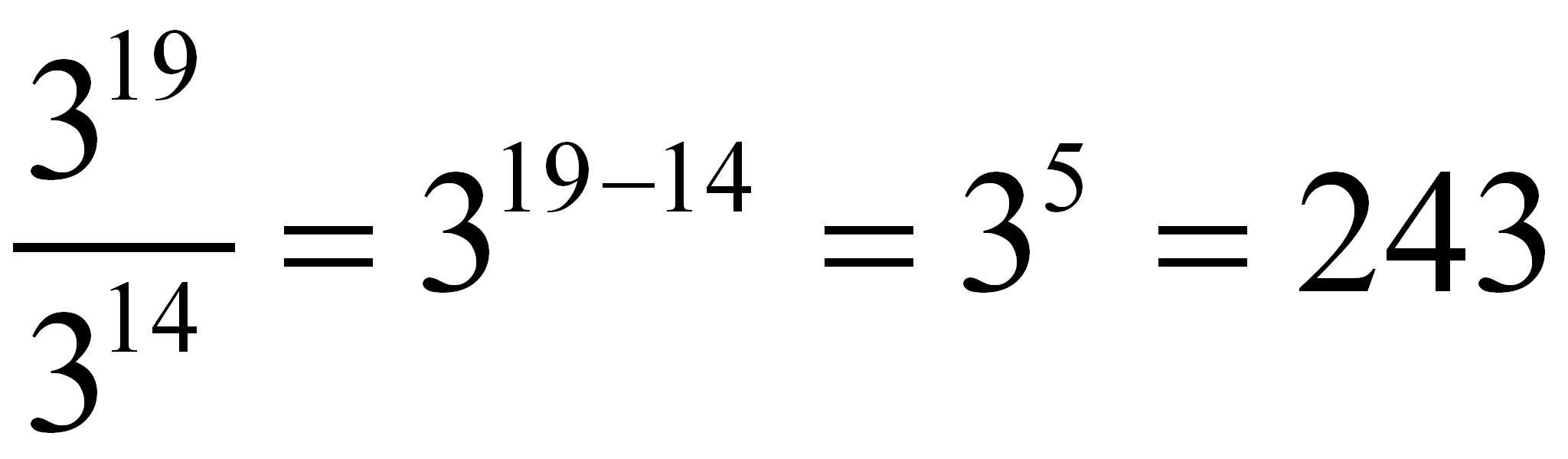
***DIVIDIR POTENCIAS DE BASE DIFERENTE: Para dividir potencias que no tienen la misma base, calculas el valor de cada una y divides sus cocientes***
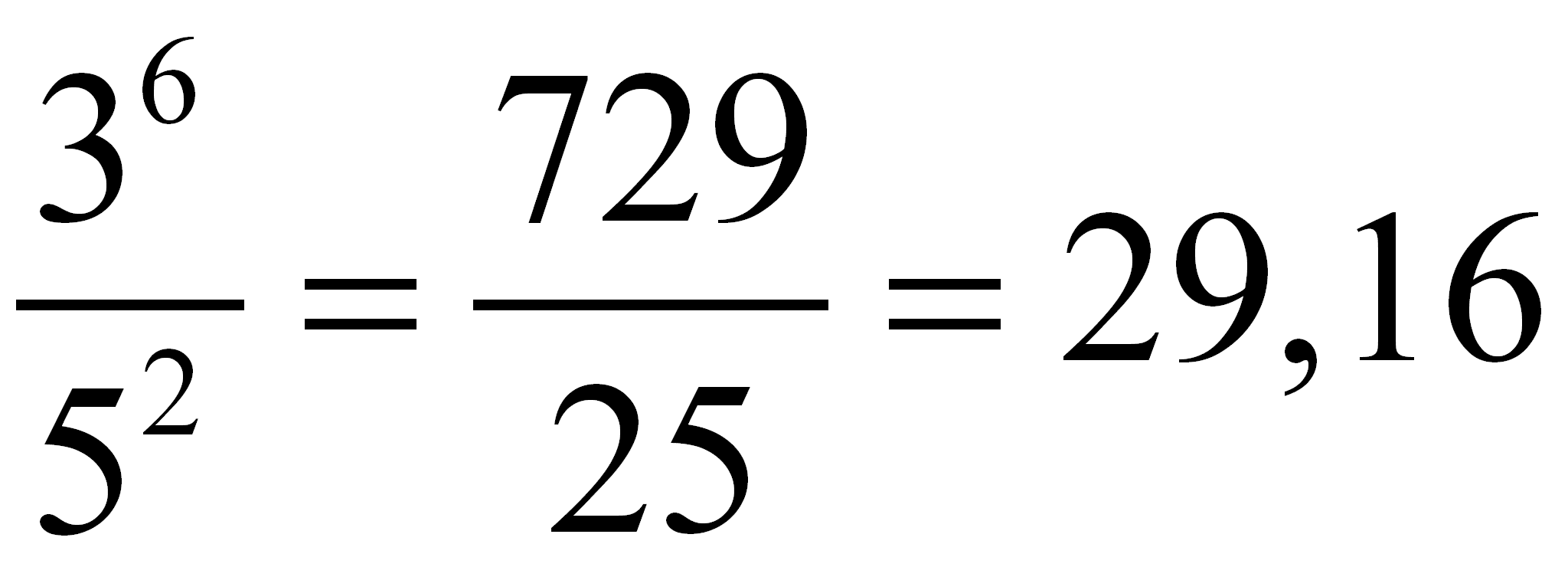
DIVIDIR POTENCIAS CON EL MISMO EXPONENTE:
Si los exponentes son iguales, puedes dividir las bases y colocar el mismo exponente:
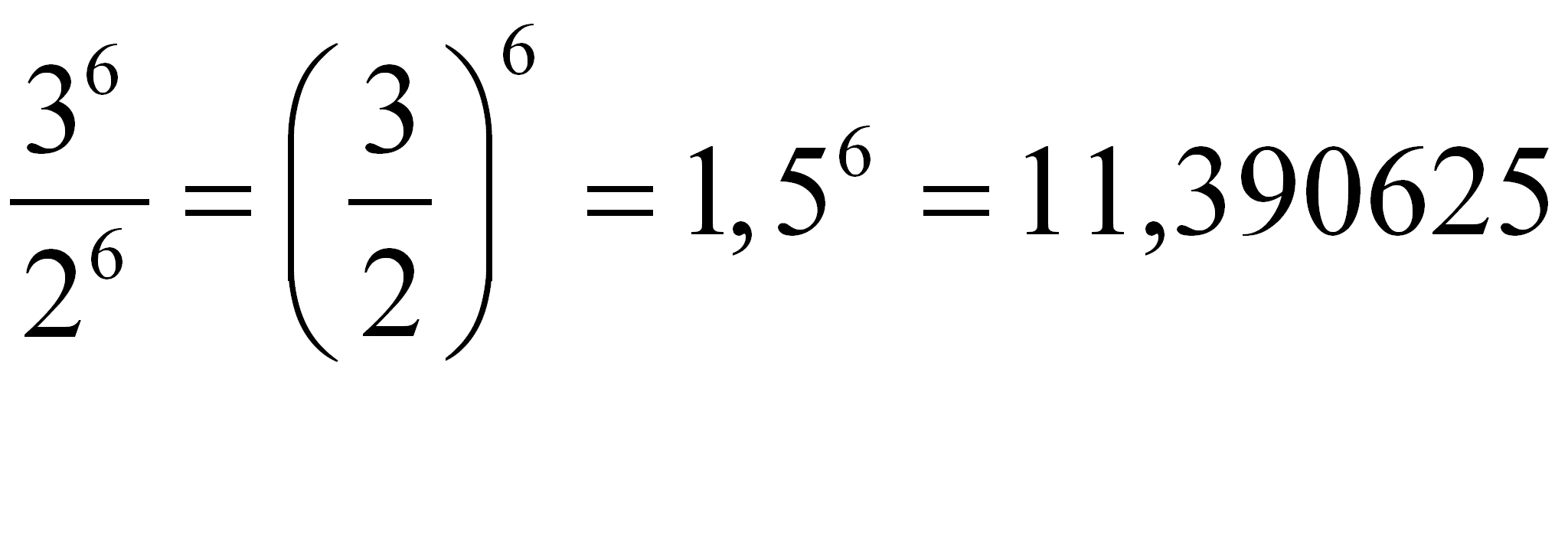
Resuelve y comprueba:
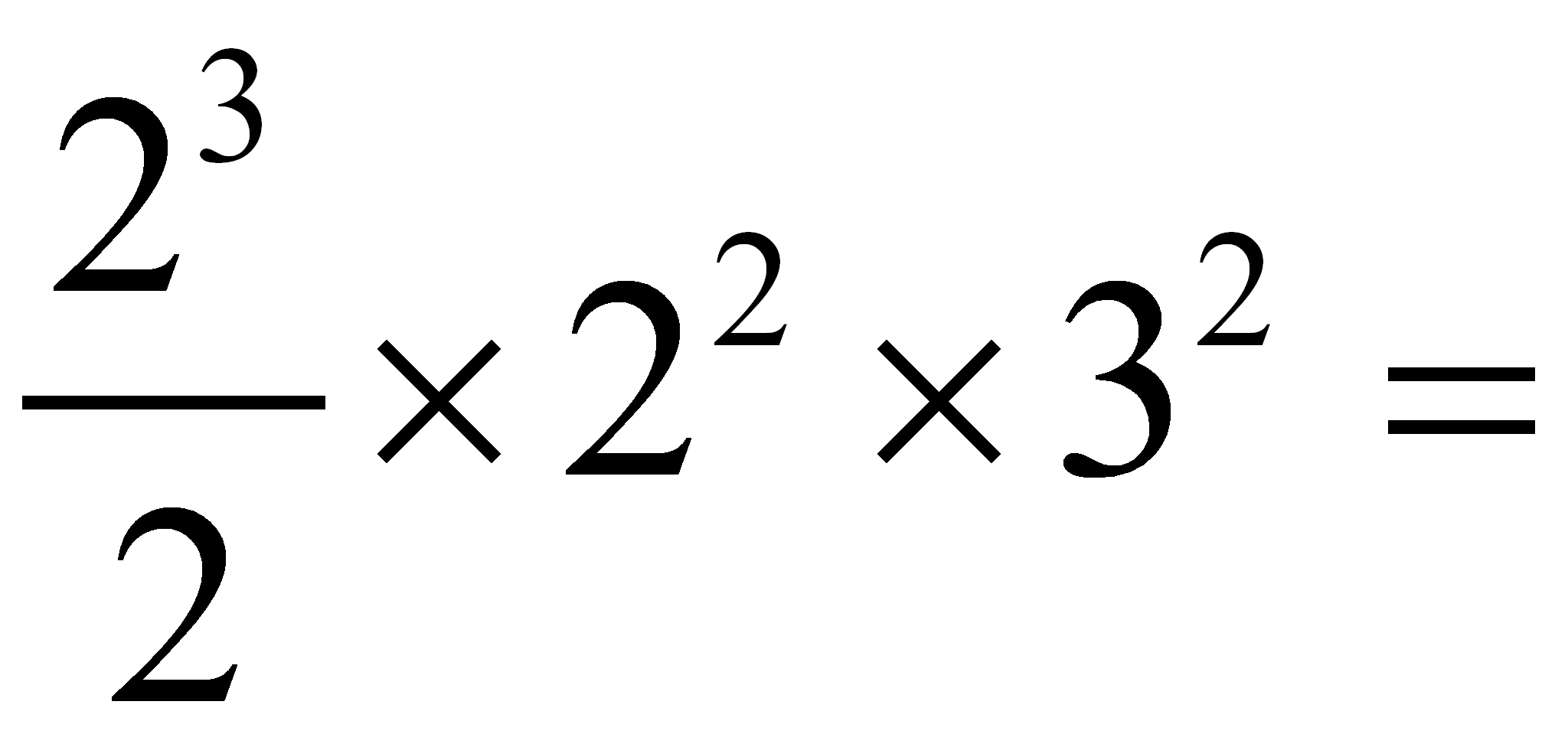
Respuesta:
1) 
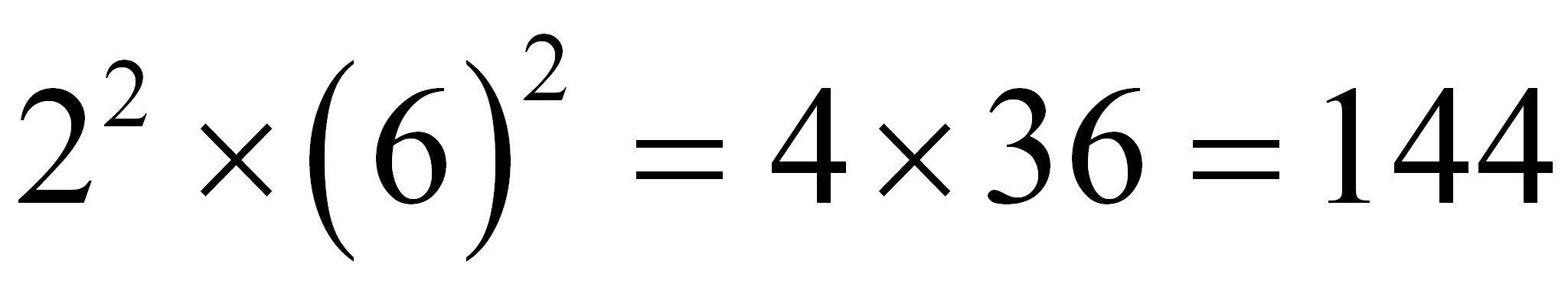
Exponentes negativos
¿Negativos? ¿Qué es lo contrario de multiplicar? ¡Dividir! Un exponente negativo significa cuántas veces se divide entre el número.
Ejemplo: 8-1 = 1 ÷ 8 = 0.125
O varias divisiones:
Ejemplo: 5-3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0.008
5-3 también se podría calcular así:
1 ÷ (5 × 5 × 5) = 1/53 = 1/125 = 0.008
ELEVAR UNA POTENCIA A OTRA POTENCIA:
Una potencia elevada a otra potencia tiene por base la misma y por exponente el producto de exponentes:
2.25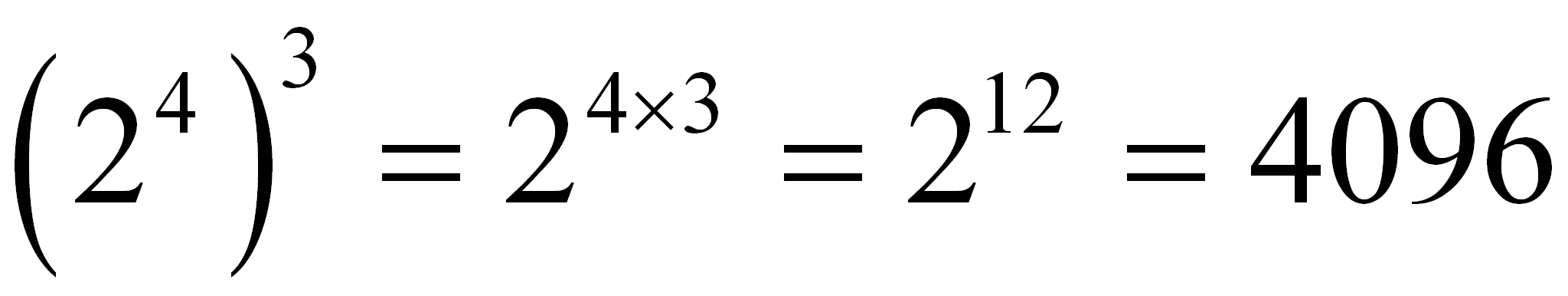 
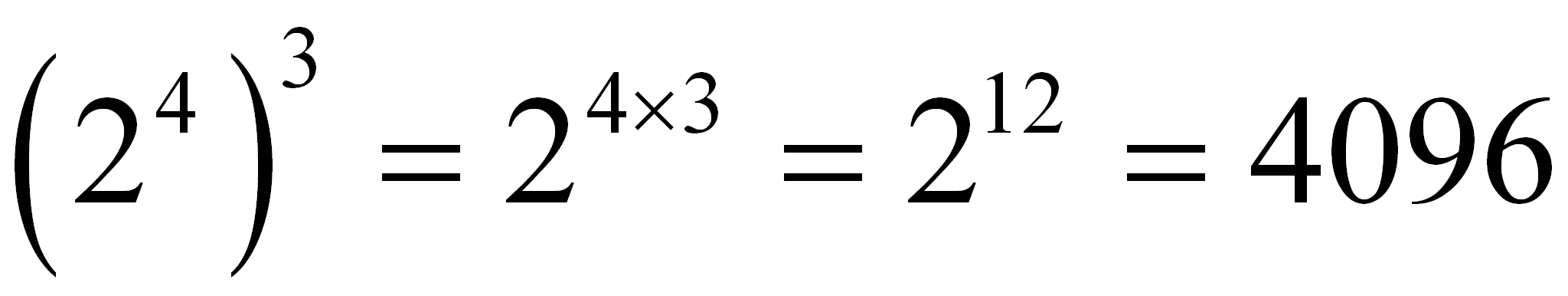
2.26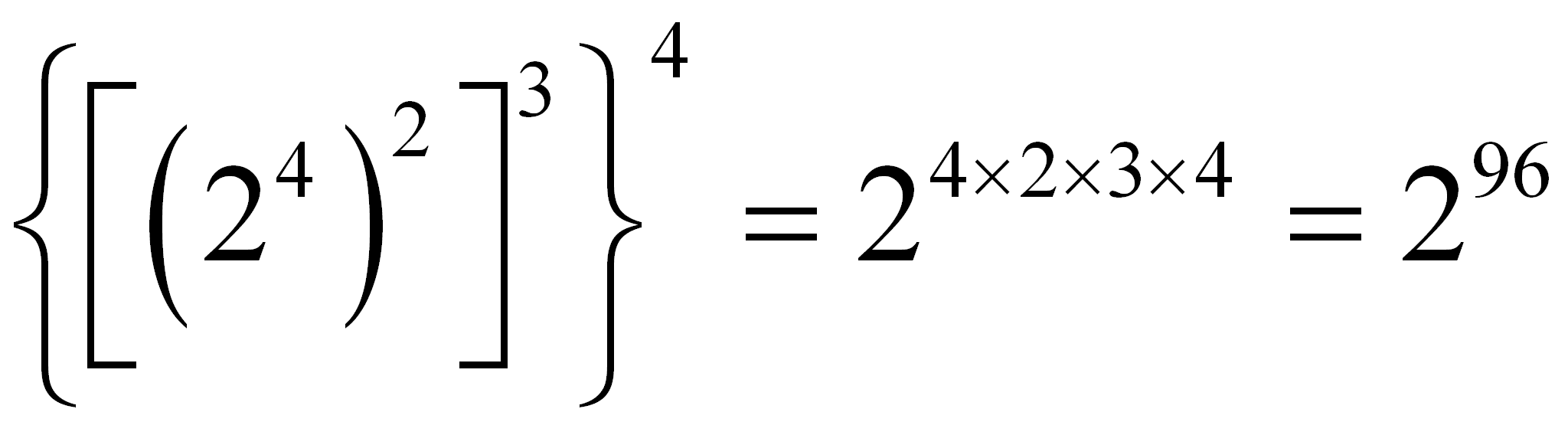 
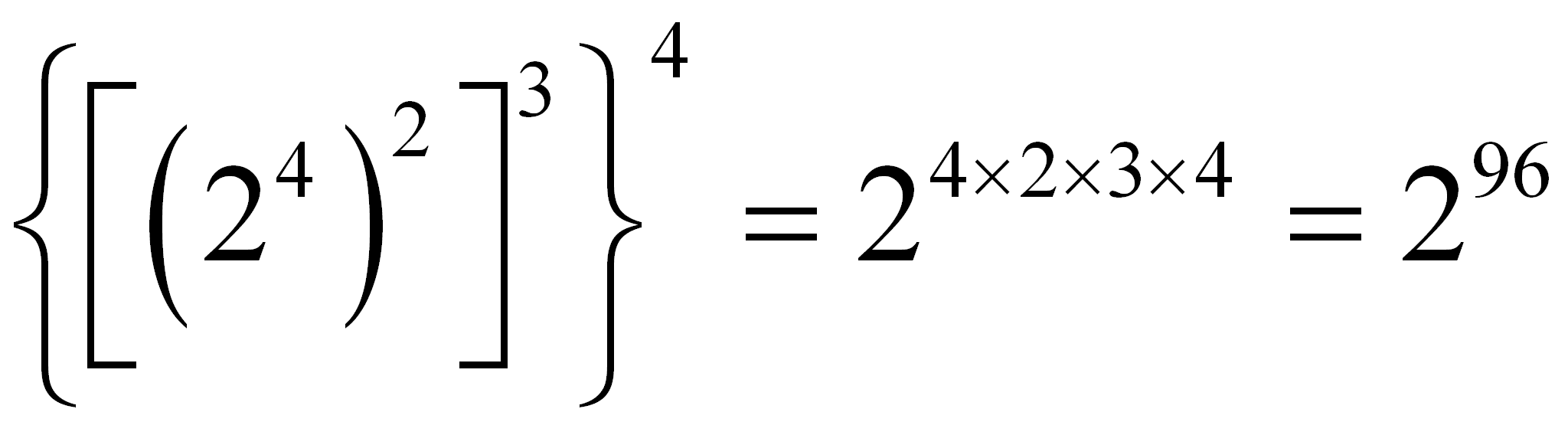
Cociente de potencias con el mismo exponente:
Es otra potencia con el mismo exponente y cuya base es el cociente de las bases.
an : bn = (a : b)n
63 : 33 = 23
POTENCIAS DE BASE NEGATIVA:
Una potencia de base negativa como:
ó
El signo del resultado depende del exponente. Si es par, el resultado es positivo y si es impar, es negativo. ¿Por qué?
(Recuerda que el asterisco (*) equivale al signo 
)
)
Si a un número negativo le multiplicas por sí mismo, es decir, dos veces, -2*-2, primero multiplicas los signos y obtendrás: menos por menos igual a más. Si vuelves a multiplicar por -2 tienes: más (del último producto) por menos igual a menos:
(-2)*(-2) = 4
(-2)*(-2)*(-2) = -8
(-2)*(-2)*(-2)*(-2) = (-8)*(-2) = 16
TAREA PARA ENTREGAR EL JUEVES 13 SEPTIEMBRE
