MATE 2. Semana del 17 al 21 septiembre 2018

Bloque: 1
Eje: FORMA, ESPACIO Y MEDIDA
Aprendizaje esperado: • Identificación de relaciones entre los ángulos que se forman entre dos rectas paralelas cortadas por una transversal. Justificación de las relaciones entre las medidas de los ángulos interiores de los triángulos y paralelogramos

Angulos en triángulos y paralelogramos

Ángulos interiores de polígonos

Un ángulo interior es un ángulo dentro de una figura.

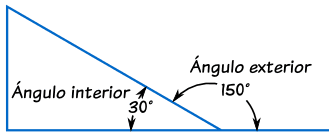
TRIÁNGULOS

Los ángulos interiores de un triángulo suman 180°

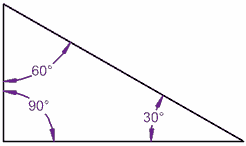90° + 60° + 30° = 180°	80° + 70° + 30° = 180°
¡En este triángulo es verdad!	Vamos a inclinar una línea 10° ... También funciona, porque un ángulo aumentó 10°, pero otro disminuyó 10°

CUADRILÁTEROS (CUADRADOS, ETC.)

(Un cuadrilátero es una figura de 4 lados)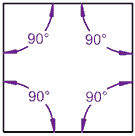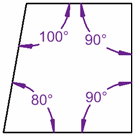

90° + 90° + 90° + 90° = 360°	80° + 100° + 90° + 90° = 360°
Un cuadrado suma 360°	Vamos a inclinar una línea 10° ... ¡también suman 360°!
Los ángulos interiores de un cuadrilátero suman 360°

PORQUE EN UN CUADRADO HAY DOS TRIÁNGULOS

Los ángulos interiores de este triángulo suman 180° (90°+45°+45°=180°)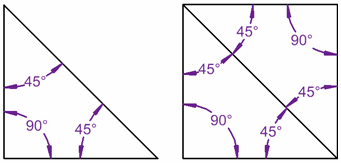

... y los de este cuadrado 360°  ... ¡porque el cuadrado está hecho de dos triángulos!

Ejemplo de problemas 1:

Ejemplo de problemas 2:

Ángulos interiores de polígonos

Un ángulo interior es un ángulo dentro de una figura.

Triángulos

Los ángulos interiores de un triángulo suman 180°

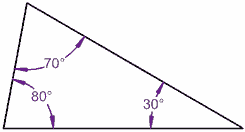90° + 60° + 30° = 180°	80° + 70° + 30° = 180°
¡En este triángulo es verdad!	Vamos a inclinar una línea 10° ... También funciona, porque un ángulo aumentó 10°, pero otro disminuyó 10°

Un ángulo interior de un triángulo lo forman dos lados.

La suma de los ángulos interiores de un triángulo es igual a 180°.

A + B + C = 180º

Un ángulo interior y exterior de un triángulo son suplementarios, es decir, suman 180º.

α = 180º - A

 Tipos de ángulos según su posición

2.1.Ángulos consecutivos

Ángulos consecutivos son aquellos que tienen el vértice y un lado común.

2.2.Ángulos adyacentes

Ángulos adyacentes son aquellos que tienen el vértice y un lado común, y los otros lados situados uno en prolongación del otro. Forman un ángulo llano.

2.3. Ángulos opuestos por el vértice:

Son los que teniendo el vértice común, los lados de uno son prolongación de los lados del otro.

Los ángulos 1 y 3 son iguales.

Los ángulos 2 y 4 son iguales.

3 Clases de ángulos según su suma

3.1.Ángulos complementarios:

Dos ángulos son complementarios si suman 90°.

3.2. Ángulos suplementarios

Dos ángulos son suplementarios si suman 180°.

4 Ángulos entre paralelas y una recta transversal

4.1. Ángulos correspondientes

Los ángulos 1 y 2 son iguales.

4.2. Ángulos alternos internos

Los ángulos 2 y 3 son iguales.

4.3. Ángulos alternos externos

Los ángulos 1 y 4 son iguales.

1. A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$x=$x, equals 

 $^\circ$

2. A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$132^\circ$$x^\circ$

$x =$x, equals

 $^\circ$

3. A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$125^\circ$$x^\circ$

$x =$x, equals

 $^\circ$

4. A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$48^\circ$$x^\circ$

$x =$x, equals

 $^\circ$

5. A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$122^\circ$$x^\circ$

$x =$x, equals

 $^\circ$

6. Dadas las relaciones:

$\qquad \overline{OA}\perp\overline{OC}$

$\qquad m \angle AOB = 6x - 12^\circ$space, m, angle, A, O, B, equals, 6, x, minus, 12, degree

$\qquad m \angle BOC = 3x + 30^\circ$space, m, angle, B, O, C, equals, 3, x, plus, 30, degree

Encuentra $m\angle AOB$m, angle, A, O, B:

$O$$A$$C$$B$

${}^{\circ}$

7. Puesto que 

$\overline{AB} \perp \overline{CD}$

$A$$B$$C$$D$$E$$F$$G$$\greenD{77^\circ}$$\blueD{x^\circ}$

NOTA: los ángulos no están necesariamente dibujados a escala.

$x =$x, equals

 $\Large{{}^\circ}$

8. 

$A$$B$$C$$D$$F$$E$$20^\circ$$25^\circ$$G$$\goldD{x^\circ}$

NOTA: los ángulos no están necesariamente dibujados a escala.

$x =$x, equals

 $\Large{{}^\circ}$

9. Las rectas w y m, cortadas por la transversal k, forman los ángulos, 1,2,3,4,5,6,7,8.

Completa:

a-) El 1 y 4 son _______________________

b-) Los ángulos 2 y 7 son ___________________

c-) Los ángulos (1,5) y (4,8) son ________________

d-) Al 3 y al 7 se le llama ____________________

e-) Los ángulos 4 y 5 son __________________

f-) Los ángulos 1 y 8 son _________________

10. Dadas las rectas p y q cortadas por la transversal r y las medidas de los ángulos dados.

Hallar:
1-) Si m< a = 58°......... m, los demás ángulos (b, c, d, e, f, g, h)

11.En la figura aparecen marcados y enumerados los ángulos del 1 al 6. Marca las proposiciones que sean correctas.

a-) El único ángulo adyacente al ángulo 1 es el ángulo 6.
b-) El único ángulo opuesto por el vértice al ángulo 2 es el ángulo 3.
c-) Los ángulos consecutivos al ángulo 3, tienen la misma amplitud            

12. En cualquier triángulo la suma de los ángulos interiores suman:

90°

180°

360°

0°

pregunta-1

13. ¿Cuánto suman los ángulos interiores de un paralelogramo?

180°

90°

360°

100°

pregunta-1

14. Los triángulos rectángulos tienen un ángulo de:

90°

180°

360°

100°

pregunta-1

15. En un triángulo rectángulo la suma de los de sus ángulos interiores es de 4x + 100. ¿Cuántos grados equivale la variable X ?

30°

40°

20°

10°

                                                                            TRIÁNGULOS
Ejercicio 1.-

En la siguiente imagen, ¿Cuál es el valor del ángulo x?
(Fig. 3)

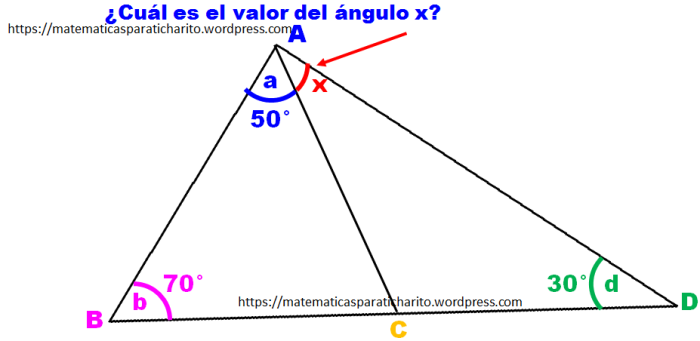
Ejercicio 2.-

En la siguiente imagen se intersectan líneas paralelas y líneas perpendiculares. ¿Cuál es el valor del ángulo “x”?
(Fig. 8)

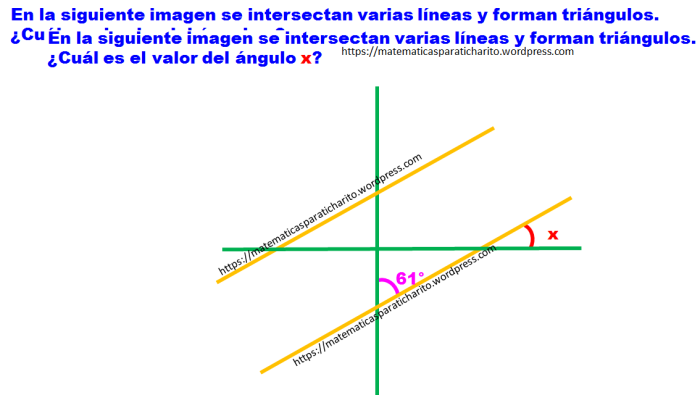
Ejercicio 3.-

Ahora tenemos otro ejercicio de ángulos internos (fig. 12).

Paralelogramos
1.- ¿Qué cuadrilátero tiene las dos diagonales iguales y sus lados son iguales dos a dos?

2.- Si los ángulos de un cuadrilátero miden, respectivamente, 80º, 110º y 70º, ¿Cuánto medirá el ángulo que falta? 
3.- ¿Cuál es el paralelogramo que tiene las diagonales perpendiculares?
4.- ¿Cómo se llama el cuadrilátero que tiene dos lados paralelos?
5.- Encuentra el área del paralelogramo que tiene 5cm de base y 3 de altura