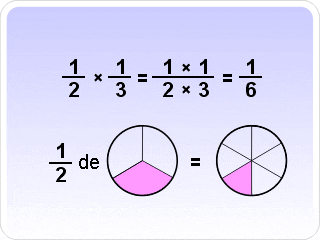MATE 1. Semana del 7al 11 octubre 2019.

BLOQUE:	1
EJE:	NÚMERO, ÁLGEBRA Y VARIACIÓN
TEMA:	Multiplicación y división
SUBTEMA:	5. Multiplicación con fracciones.
APRENDIZAJES ESPERADOS	• Resuelve problemas de multiplicación con fracciones y decimales y de división con decimales

1. Multiplicación de fracciones

OBSERVA  y analiza cada situación

1. 
2. 
3. 

¿Cómo resolver una multiplicación de fracciones?

Para multiplicar fracciones tenemos que seguir la siguiente regla:

1.  Multiplicamos los numeradores de la fracciones y colocamos el resultado en el numerador.
2. Multiplicamos los denominadores y colocamos el resultado en el denominador.
3. se simplifica si es posible.   

1.1- Resolución de problemas 

Ejemplo:

Don José dejó 3/5 de la pared para pintar con colores cálidos. Si pintará de color café 2/3 de lo destinado a los colores cálidos, ¿qué parte de la pared será de color café?

Si representamos gráficamente la información tenemos:

Por lo tanto, se tiene que 2/5 de la pared serán pintados de color café.

1.2- Multiplicación de números naturales y fracciones

Debes hacer lo siguiente:

Resolver el siguiente problema:

En una tienda hay 80 botellas de agua de 1/4 L cada una. ¿Cuántos litros de agua hay en total?

Respuesta: En total hay 20 L de agua en la tienda.

2- División de fracciones

Para dividir 2 fracciones, se multiplican sus términos en cruz, es decir, se multiplica el numerador de la primera fracción con el denominador de la segunda. Luego se multiplica el denominador de la primera fracción por el denominador de la segunda.
 

Ejemplo:

 

 

Otra forma de dividir fracciones es multiplicar la primera fracción por la inversa de la segunda.

Ejemplo:

 

 

 

2.1- División de números naturales y fracciones

Si el segundo término es un número natural, se multiplica por la fracción inversa de ese número.

Ejemplo:

 

 

 

 

 

 

- Los números mixtos se deben expresar como fracciones impropias antes de dividir.

- También se pueden simplificar antes de realizar las multiplicaciones. Por ejemplo:

 

Resuelve los siguientes ejercicios.

1. 12/9 X 3/8 =   
2. 2/3 X 6 = 
3. 1/2 X 10 = 
4. 4/5 X 20 = 
5. 3/2 X 18 = 
6. 1/6 X 24 = 
7. 3/9 X 2/5 = 
8. 6/8 X 4/6 = 
9. 3/4 X 2/3 =  
10. 4/5 X 9/12 =  
11. 1/6 X 13 = 
12. 4/7 X 3/5 = 
13. 7/8 X 2/6 = 
14. 3/5 X 2/3 = 
15. 2/5 X 3/7 = 

1. Calcular los siguientes productos de un natural por una fracción:

2. Calcular las siguientes divisiones de una fracción y un número:

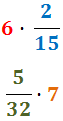
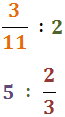
Problema 3

Calcular los siguientes productos de fracciones:

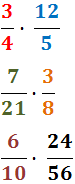
Problema 4

Calcular las siguientes divisiones de fracciones:

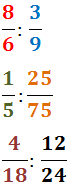
Problema 5

Calcular x para que se cumplan las igualdades (resolver las ecuaciones):

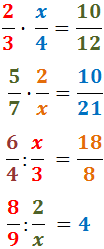
Problema 6

¿Qué fracción del total es la mitad de una tercera cuarta parte?

Problema 7

Calcular cuánto son dos tercios de tres quintas partes.

Problema 8

Simplificar la siguiente fracción de fracciones:

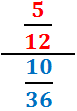
Problema 9

Usamos tres quintas partes del agua de un depósito que sólo contiene tres octavas partes de su capacidad total. Calcular la fracción de agua que hemos usado con respecto a la capacidad del depósito.

Problema 10

Calcular el siguiente cociente de cocientes:

Resuelve las siguientes divisiones

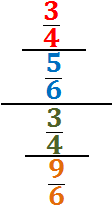
1)	3/5 : 2/6 =
2)	6/4 : 4/8 =
3)	9/2 : 7/3 =
4)	7/4 : 4/5 =
5)	2/8 : 6/2 =
6)	4/9 : 9/2 =
7)	7/7 : 1/2 =
8)	4/9 : 3/4 =
9)	4/3 : 1/6 =
10)	4/7 : 2/6 =