MATE 1. Semana del 4 al 8 octubre 2019
|
BLOQUE :
|
1
|
|
EJE:
|
Forma, espacio y medida
|
|
TEMA:
|
Magnitudes y medidas
|
|
SUBTEMA:
|
9. Perímetro de polígonos 10. Área de triángulos y
cuadriláteros
|
|
APRENDIZAJES ESPERADOS:
|
• Calcula el perímetro de polígonos y del círculo, y
áreas de triángulos y cuadriláteros desarrollando y aplicando fórmulas.
|
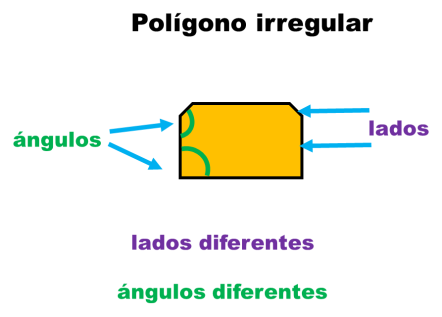
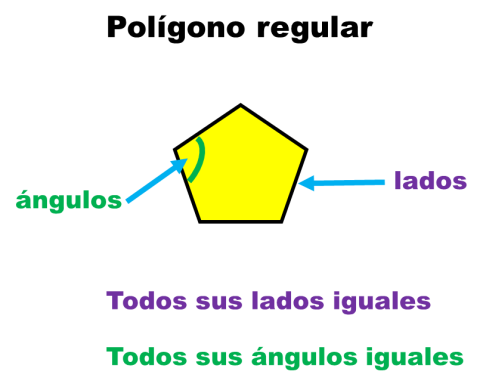
Polígono regular
Recordemos que un polígono es regular cuando todos sus lados son iguales y todos sus ángulos también lo son. Es irregular si no cumple con estas condiciones.

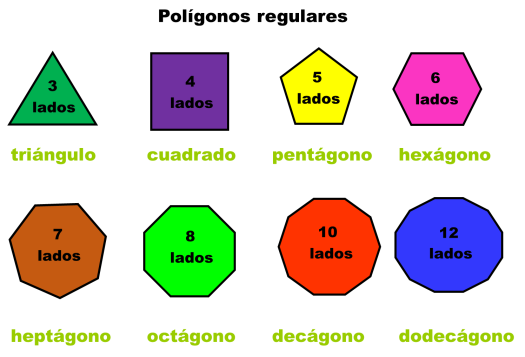
Nombres de polígonos regulares
Tres lados………..triángulo o trígono
Cuatro lados……cuadrado o tetrágono
Cinco lados…….pentágono
Seis lados………hexágono
Siete lados……heptágono o septágono
Ocho lados……octágono
Nueve lados…..nonágono o eneágono
Diez lados…….decágono
Once lados…..endecágono o undecágono
Doce lados….dodecágono
Trece lados….tridecágono
Catorce lados…tetradecágono
Quince lados….pentedecágono
Dieciséis lados……hexadecágono
Diecisiete lados….heptadecágono
Dieciocho lados….octadecágono
Diecinueve lados…eneadecágono
Veinte lados…icoságono
Treinta lados….triacontágono
cuarenta lados…..tetracontágono
100 lados….hectágono
1000 lados…..chiliágono
Cuatro lados……cuadrado o tetrágono
Cinco lados…….pentágono
Seis lados………hexágono
Siete lados……heptágono o septágono
Ocho lados……octágono
Nueve lados…..nonágono o eneágono
Diez lados…….decágono
Once lados…..endecágono o undecágono
Doce lados….dodecágono
Trece lados….tridecágono
Catorce lados…tetradecágono
Quince lados….pentedecágono
Dieciséis lados……hexadecágono
Diecisiete lados….heptadecágono
Dieciocho lados….octadecágono
Diecinueve lados…eneadecágono
Veinte lados…icoságono
Treinta lados….triacontágono
cuarenta lados…..tetracontágono
100 lados….hectágono
1000 lados…..chiliágono
Diagonales
Se llama diagonal al segmento determinado por dos vértices no consecutivos o contiguos.
Si desde un vértice cualquiera se trazan todas las diagonales posibles, siempre habrá tres vértices a los cuales no se puede trazar diagonal: el vértice desde el cual se trazan las diagonales y los dos vértices contiguos (con los que se forman lados).
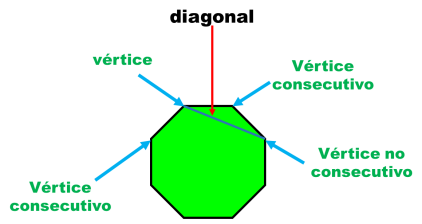
Por ello, el número de diagonales que pueden trazarse desde un vértice es igual al número de lados menos 3.
Si desde un vértice cualquiera se trazan todas las diagonales posibles, siempre habrá tres vértices a los cuales no se puede trazar diagonal: el vértice desde el cual se trazan las diagonales y los dos vértices contiguos (con los que se forman lados).

Por ello, el número de diagonales que pueden trazarse desde un vértice es igual al número de lados menos 3.
Elementos de un polígono regular
Centro
Es su punto interior que equidista de cada vértice, es decir, la distancia del centro a cualquiera de sus vértices es igual, así como la distancia a cualquiera del centro de sus lados.
Es su punto interior que equidista de cada vértice, es decir, la distancia del centro a cualquiera de sus vértices es igual, así como la distancia a cualquiera del centro de sus lados.
Radio
Es el segmento que va del centro a cada vértice. Se identifica con la letra r

Apotema
Distancia del centro al punto medio de cada lado, se identifica con la letra a. Es la altura de cualquiera de los triángulos iguales en los que se puede descomponer el polígono, considerando el lado como base.

Es el segmento que va del centro a cada vértice. Se identifica con la letra r

Apotema
Distancia del centro al punto medio de cada lado, se identifica con la letra a. Es la altura de cualquiera de los triángulos iguales en los que se puede descomponer el polígono, considerando el lado como base.

Perímetro del polígono regular
Es la suma de los valores de sus lados.
Cuando el polígono es regular, como todos sus lados son iguales, el perímetro se obtiene multiplicando el valor de un lado por el número de lados que tiene el polígono.

Cuando el polígono es regular, como todos sus lados son iguales, el perímetro se obtiene multiplicando el valor de un lado por el número de lados que tiene el polígono.

Área del polígono regular
Si del centro se trazan radios a todos sus vértices, el polígono queda dividido en tantos triángulos iguales como lados tiene el polígono.

El área del polígono será igual al área de un triángulo multiplicada por el número de triángulos.
Si el lado del polígono se nombra l y la altura de cada triángulo es el apotema del polígono identificada como a, el área de cada uno de los triángulos será:
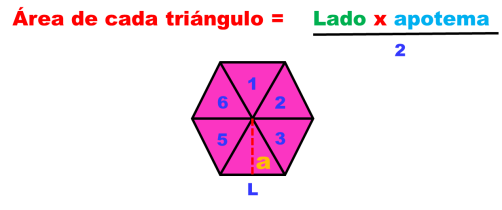
Si el polígono tiene n lados, el número de triángulos que se formarán será igual a n.
Entonces:

Pero n x l significa el número de lados (n) por el valor de un lado (l) del polígono; que si recuerdas, es la fórmula para obtener el perímetro del polígono regular.
Por eso la fórmula que se utiliza para obtener el área de un polígono regular es igual a la mitad del producto del perímetro por el apotema


El área del polígono será igual al área de un triángulo multiplicada por el número de triángulos.
Si el lado del polígono se nombra l y la altura de cada triángulo es el apotema del polígono identificada como a, el área de cada uno de los triángulos será:

Si el polígono tiene n lados, el número de triángulos que se formarán será igual a n.
Entonces:

Pero n x l significa el número de lados (n) por el valor de un lado (l) del polígono; que si recuerdas, es la fórmula para obtener el perímetro del polígono regular.
Por eso la fórmula que se utiliza para obtener el área de un polígono regular es igual a la mitad del producto del perímetro por el apotema


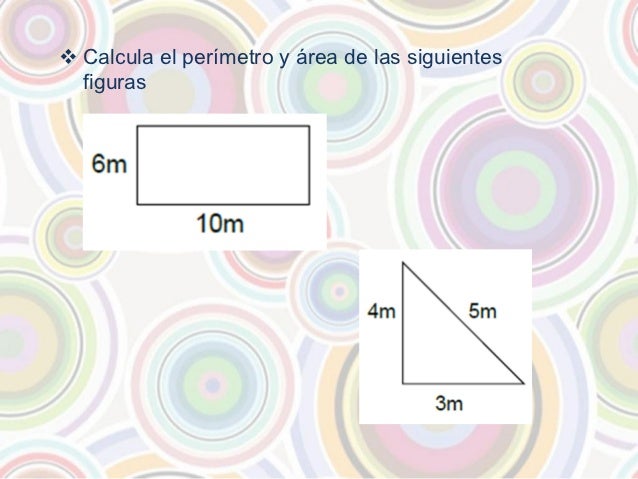
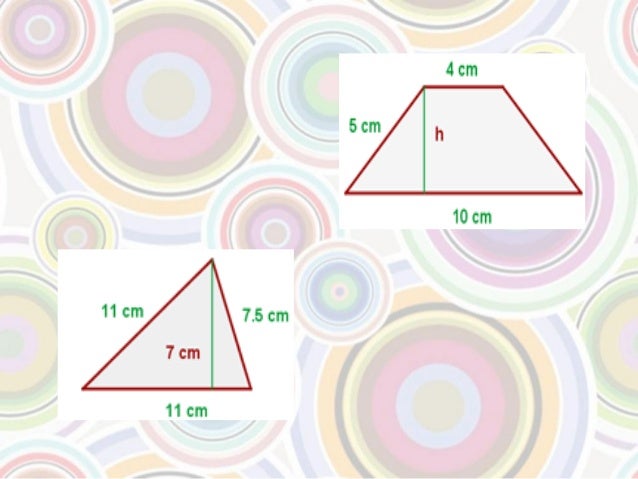
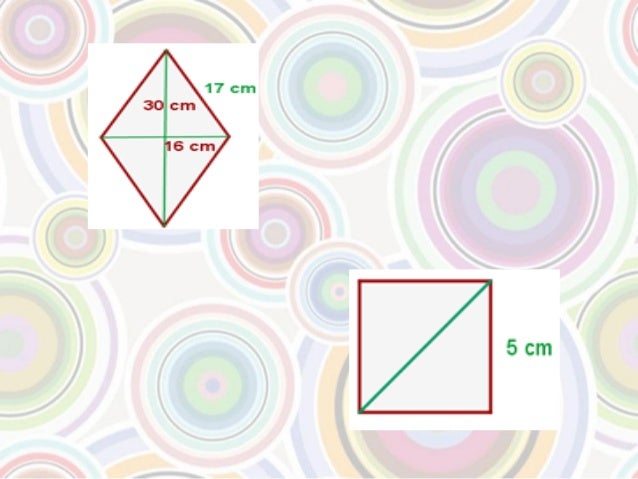
1)
Halla el perímetro y el área de un cuadrado de 3 m
de lado.
2) Halla el perímetro y
el área de un cuadrado de 11,3 m de lado.
3)
Averigua el área de un cuadrado cuyo perímetro mide
29,2 cm.
4) El perímetro de un rectángulo es 20,4 dm. Si uno de sus lados mide 6,3 dm, halla el área.
5) El área de un rectángulo es 6384 decímetros cuadrados. Si la base mide 93 cm, ¿cuánto mide la altura? y ¿cual es su perímetro?.
21. Calcular el perímetro de un octágono regular que mide 32 cm de lado