MATE 1. Semana del 28 octubre al 1º noviembre 2019

BLOQUE:	1
EJE:	Forma, espacio y medida
TEMA:	Figuras y cuerpos geométricos
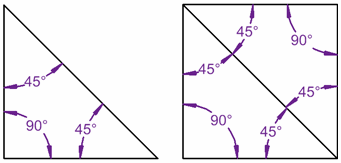
SUBTEMA:	8. Suma de los ángulos interiores de triángulos y de cuadriláteros.
APRENDIZAJES ESPERADOS:	• Analiza la existencia y unicidad en la construcción de triángulos y cuadriláteros, y determina y usa criterios de congruencia de triángulos.

Ángulos interiores de polígonos

Un ángulo interior es un ángulo dentro de una figura.

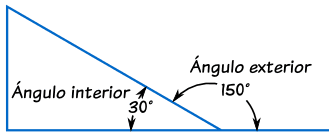
Suma de ángulos interiores y exteriores de un triangulo

a)

Los ángulos interiores de un triángulo suman 180°

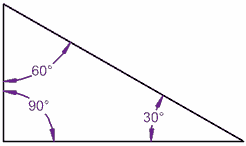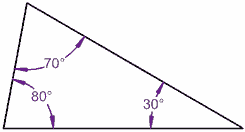90° + 60° + 30° = 180°	80° + 70° + 30° = 180°

En un triángulo existen dos tipos de ángulos: los ángulos interiores lo forman dos lados y los ángulos exteriores lo forman un lado y su prolongación.

Suma de ángulos interiores y exteriores de un cuadrilátero

Un cuadrilátero es un polígono de cuatro lados, los ángulos interiores de un cuadrilátero suman 360°

Un cuadrado suma 360° , 90° + 90° + 90° + 90° = 360°

ACTIVIDAD

Vamos a demostrar  de forma práctica que los ángulos interiores de un triángulo suman 180º. A partir de ahí veremos cómo calcular cuánto suman los ángulos interiores de cualquier polígono. Por el camino aprenderemos un montón de cosas más sobre geometría.

Materiales:

• Papel o cartulina.
• Tijeras.
• Regla.
• Compás, plato o cualquier otro objeto con el que dibujar un círculo.
• Rotuladores (plumones) o lápices de colores.

Procedimiento:

• Dibuja un círculo grande en una hoja.
• Divide el círculo en 2 partes iguales trazando un diámetro. El diámetro representa un ángulo llano, es decir, de 180°.

Aunque también dibujamos el ángulo recto y la vuelta completa, con el ángulo llano es suficiente para realizar esta actividad.

• Dibuja distintos triángulos en una hoja de papel o cartulina y recórtalos. Marca los ángulos y etiqueta con números.

• Con cada triángulo, recorta los ángulos y colócalos sobre el ángulo llano unidos por el vértice.
• ¿Qué ocurre? ¡Exacto!, la suma de los ángulos de cualquier triángulo es siempre 180°.

EJERCICIOS

Elige la opción correcta:

1De un triángulo cualquiera sabemos que tiene un ángulo de 35° y otro de 83°, entonces el tercer ángulo mide...

62°.

52°.

242°.

2El triángulo del ejercicio anterior es...

acutángulo.

rectángulo.

obtusángulo.

3Un triángulo isósceles cuyos ángulos iguales miden 45° cada uno es un triángulo...

acutángulo.

rectángulo.

obtusángulo.

4La suma de dos lados de un triángulo son 15 cm, entonces el otro lado puede medir...

18 cm.

12 cm.

16 cm.

5Sabemos que la medida de dos lados de un triángulo son 2 cm y 5 cm. Entonces, el tercer lado podrá medir...

entre 0 y 7 cm.

más de 3 cm.

más de 3 cm y menos de 7 cm.

6La medida del ángulo exterior marcado en este dibujo es... 

71°.

261°.

251°.

7La medida del ángulo interior del triángulo anterior es que falta es...

109°.

33°.

Faltan datos para resolver el problema.

8Si tenemos un triángulo equiátero cuyo perímetro es de 15 cm, su lado mide...

5 cm.

3 cm.

Faltan datos para resolver el problema.

9Sabemos que uno de los ángulos agudos de un triángulo rectángulo mide 52° 57', entonces el otro ángulo agudo mide...

37° 3'.

38° 3'.

Faltan datos para resolver el problema.

10. ¿Qué cuadrilátero tiene las dos diagonales iguales y sus lados son iguales dos a dos? Rectángulo 
11.- Si los ángulos de un cuadrilátero miden, respectivamente, 80º, 110º y 70º, ¿Cuánto medirá el ángulo que falta? 100º 
12.- ¿Cuál es el paralelogramo que tiene las diagonales perpendiculares? Rombo 
13.- ¿Cómo se llama el cuadrilátero que tiene dos lados paralelos? Trapecio

14.



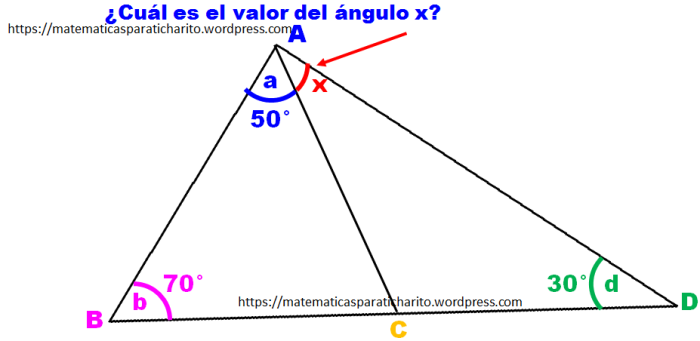
15. En la siguiente imagen se intersectan líneas paralelas y líneas perpendiculares. ¿Cuál es el valor del ángulo “x”?




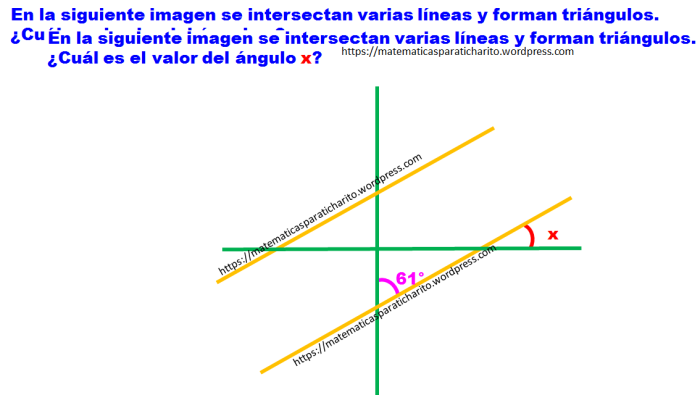
16.

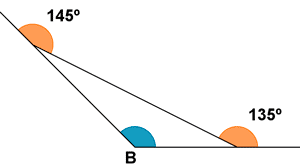
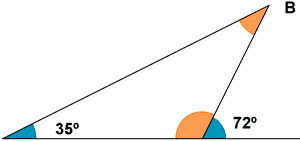
Calcula la medida del ángulo  B  de los siguientes polígonos.

a)              b)

17)    Calcula la medida del ángulo  B  de los siguientes polígonos :

a)             b)

18)    Calcula la medida del ángulo  B  en los siguientes polígonos :

a)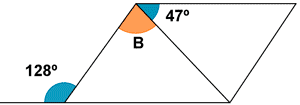             b)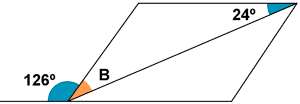

19)    Calcula la medida de los ángulos desconocidos de los siguientes polígonos.

a) 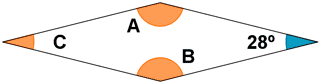              b) 

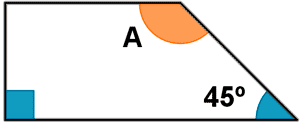c)                     d)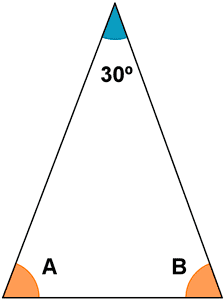 

Cuánto mide el ángulo $x$x?

$x$$116^{\circ}$$3.3$$3.3$$3.3$$3.3$

¿Cuánto mide el ángulo $x$x?

$x$$34^{\circ}$$23.6$$10.7$$24.9$$11.8$

¿Cuánto mide el ángulo $x$x?

$x$$113^{\circ}$$10.8$$16.1$$10.8$$16.1$

¿Cuánto mide el ángulo $x$x?

$x$$146^{\circ}$$23.9$$12.0$$23.9$$12.0$

¿Cuánto mide el ángulo $x$x?

$x$$146^{\circ}$$20.1$$10.1$$36.8$$10.1$

¿Cuánto mide el ángulo $x$x?

$48^{\circ}$$x$$25.4$$12.7$$8.4$$12.7$

¿Cuánto mide el ángulo $x$x?

$116^{\circ}$$x$$4.0$$2.8$$2.8$$4.0$