MATE 1. Semana del 14 al 18 octubre 2019

BLOQUE:	Servicios Educativos Integrados al Estado de México Dirección de Educación Secundaria y Servicios de Apoyo Departamento de Educación Secundaria en el Valle de México 1
EJE:	Forma, espacio y medida
TEMA:	Figuras y cuerpos geométricos
SUBTEMA:	7. Ángulos entre dos rectas paralelas cortadas por una transversal
APRENDIZAJES       ESPERADOS:	• Analiza la existencia y unicidad en la construcción de triángulos y cuadriláteros, y determina y usa criterios de congruencia de triángulos.

Relaciones entre parejas de ángulos

En casi todas las figuras geométricas donde intervengan rectas aparecen ángulos, los cuales es posible relacionar en cuanto a sus dimensiones y a su posición en el plano.

Así, dos ángulos pueden ser entre sí complementarios, suplementarios o adyacentes.

Dos ángulos son complementarios si la suma de sus medidas es 90°1 + 2 son complementarios, ya que:
1 + 2= 90°

Dos ángulos son suplementarios si la suma de sus medidas es 180°1 + 2 son complementarios, ya que:
1 + 2= 180°

Dos ángulos son adyacentes si tienen un lado en común y los otros dos están en la misma recta.Los ángulos adyacentes son suplementarios.

Rectas secantes y paralelas
Como ya vimos, por definición, un ángulo es una figura geométrica formada en una superficie por dos líneas rectas que parten de un mismo punto.

Fijando nuestra atención en las rectas, sabemos que estas pueden ser secantes (que se cortan) o paralelas (que no se cortan nunca).
Dos rectas secantes se cortan en un punto y determinan cuatro ángulos. Cada ángulo tiene dos lados y un vértice.


Ángulos opuestos por el vértice.
Son los ángulos formados por dos rectas que se cortan en un punto llamado vértice (V).

Los ángulos opuestos por el vértice son iguales.

Si el angulo # 1 mide 45 grado, entonces el angulo # 2 también tiene 45 grado, ya que los dos son apuesto por el vértice.

< 1 = < 2

< 3 = < 4

Ángulos determinados por dos rectas paralelas y una secante.

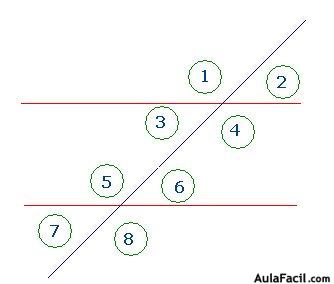
Cuando dos rectas paralelas es cortadas por una tercera recta secante, se forman 8 ángulos,

Esta distribución permite caracterizar parejas de ángulos según su posición, haciendo notar que los ángulos 3, 4, 5, y 6 son internos y que los ángulos 1, 2, 7, 8 son externos.

También se puede deducir que:
-Los ángulos 1 y 5 son correspondientes.

-Los ángulos 1 y 3 son opuesto.

-Los ángulos 1 y 2 son adyacentes.

-Los ángulos 5 y 8 son opuesto.

-Los ángulos 5 y 6 son adyacentes.

...y así sucesivamente.

Ejemplos:
Das las rectas p y q cortadas por la transversal r y las medidas de los ángulos dados

Hallar:
1-) Si medida de angulo  a = 70°......... m
2-) Si medida de angulo b = 110°......... m
3-) Si medida de angulo b = 110°......... m
4-) Si medida de angulo a = 70°......... m
5-) Si medida de angulo c = 110°......... m
Respuesta:
Como el angulo "a" y "e" son correspondiente, entonces a=e
Como "e" y "h" son opuesto, entonces como e=70°, también h=70°

TAMBIÉN...
Ángulos correspondientes:

Ángulos internos (3, 4, 5 y 6)

Ángulos externos (1, 2, 7 y 8)

I-) Las rectas w y m, cortadas por la transversal k, forman los ángulos, 1,2,3,4,5,6,7,8.

Completa:

a-) El 1 y 4 son _______________________

b-) Los ángulos 2 y 7 son ___________________

c-) Los ángulos (1,5) y (4,8) son ________________

d-) Al 3 y al 7 se le llama ____________________

e-) Los ángulos 4 y 5 son __________________

f-) Los ángulos 1 y 8 son _________________

II-) Das las rectas p y q cortadas por la transversal r y las medidas de los ángulos dados.

Hallar: La medida de todos los ángulos b, c,d, e, f, g, h.
1-) Si < a = 58°

III-) En la figura aparecen marcados y enumerados los ángulos del 1 al 6. Marca las proposiciones que sean correctas.

a-) El único ángulo adyacente al ángulo 1 es el ángulo 6.
b-) El único ángulo opuesto por el vértice al ángulo 2 es el ángulo 3.
c-) Los ángulos consecutivos al ángulo 3, tienen la misma amplitud.

IV-) Según los ángulos que se forman entre las paralelas y la secante, colocar los nombres de cada ángulo.

 

1)  < a _________________
2) < b _________________

3) < c _________________

4) < d _________________

5) < e _________________

6) < f _________________

7) < g _________________

8) < h _________________

Observa la figura siguiente y después, contesta a las preguntas siguientes:

1. ¿Cómo son los ángulos 1 y 2?
2. ¿Cómo podemos llamar a los ángulos 1 y 4?
3. ¿Son suplementarios los ángulos 2 y 4?
4. ¿Son iguales los ángulos 2 y 3? ¿Por qué?
5. ¿Son correspondientes los ángulos 3 y 7?
6. ¿Cómo son los ángulos 4 y 6?
7. ¿Es el ángulo 6  correspondiente al ángulo 3?
8. ¿Son iguales los ángulos 5 y 8? ¿Por qué?
9. ¿Cómo puedes llamarles a los ángulos 1 y 

A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$34^\circ$$x^\circ$

$x =$x, equals

 $^\circ$

A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$89^\circ$$x^\circ$

$x =$x, equals

 $^\circ$

A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$53^\circ$$x^\circ$

$x =$x, equals

 $^\circ$

A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$116^\circ$$x^\circ$

$x =$x, equals

 $^\circ$

A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$106^\circ$$x^\circ$

$x =$x, equals

 $^\circ$

A continuación se muestran dos rectas paralelas y una tercera recta que las interseca.

$76^\circ$$x^\circ$

$x =$x, equals

 $^\circ$

Determinar medidas de ángulos entre rectas que se intersecan

Problema

$A$$B$$C$$D$$E$$F$$G$$\greenD{73^\circ}$$\blueD{x^\circ}$

NOTA: los ángulos no están necesariamente dibujados a escala.

$x =$x, equals

 $\Large{{}^\circ}$

Problema

$A$$B$$C$$D$$x^\circ$$115^\circ$$\goldD{160^\circ}$$E$$F$$G$

NOTA: los ángulos no están necesariamente dibujados a escala.

$x =$x, equals

 $\Large{{}^\circ}$