MATE 2. Semana del 30 Abril al 4 Mayo 2018
Forma, espacio y medida
Medida
• Caracterización de ángulos inscritos y centrales en un círculo, y análisis de sus relaciones.
TAREA PARA ENTREGAR EL VIERNES 4 MAYO
º
º
º
Medida
• Caracterización de ángulos inscritos y centrales en un círculo, y análisis de sus relaciones.

Central
| |
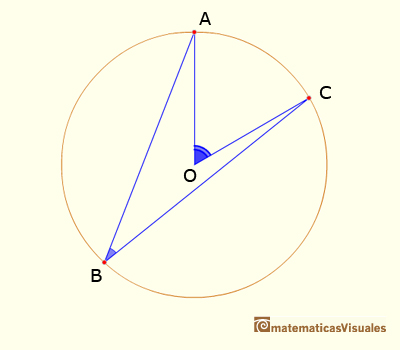
Dados dos puntos en una circunferencia, los radios desde el centro de la circunferencia a esos dos puntos forman un ángulo central.
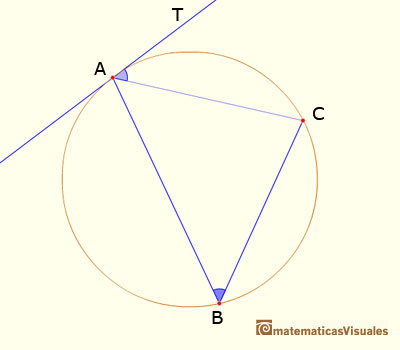
Un ángulo inscrito es un ángulo subtendido en un punto de la circunferencia por otros dos puntos de la circunferencia. Un ángulo inscrito está definido por dos cuerdas de una circunferencia que tienen un extremo común.
Euclides enumera las siguientes proposiciones, entre otras, referidas a la circunferencia:
III.20. En una circunferencia, el ángulo cuyo vértice está en el centro es el doble del ángulo cuyo vértice está en la circunferencia cuando los rayos que forman el ángulo cortan a la circunferencia en los misos dos puntos.
Esta proposición también se llama Teorema del ángulo central: El ángulo central subtendido por dos puntos de una circunferencia es el doble que cualquier ángulo inscrito subtendido por esos dos puntos.
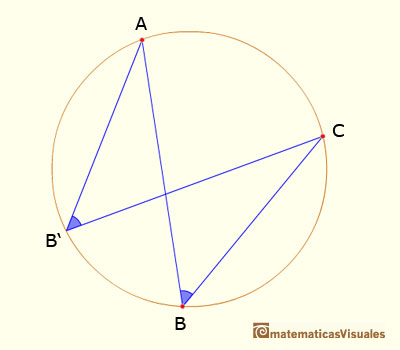
III.21. En una circunferencia, una cuerda subtiende ángulos iguales cuando los vértices están en cualquier punto de uno de los dos arcos que determina la cuerda.
III.32. Si desde el punto de contacto de una tangente a una circunferencia se traza una cuerda de ésta, el ángulo que forman la tangente y la cuerda es igual al ángulo que subtiende la cuerda y cuyo vértice está en cualquier punto de la pare de la circunferencia que queda en el lado distante de la cuerda.
 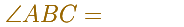 | |
TAREA PARA ENTREGAR EL VIERNES 4 MAYO
Elige la opción correcta:
1Dos cuadrantes consecutivos forman un ángulo central de...
2La medida del arco que se define al trazar el ángulo anterior es de...
3Un ángulo inscrito que abarca un arco de 30°...
4Un ángulo inscrito de 20º define un arco de...
Resuelve las siguientes cuestiones:
5Si dividimos una circunferencia en 5 arcos iguales, ¿cuánto mide cada uno de esos arcos?
¿Y cada una de los ángulos centrales correspondientes a dichos arcos?
°
6Si dividimos la circunferencia en partes iguales y el ángulo central de cada una de las partes es de 36º, ¿en cuántas partes se ha dividido la circunferencia?
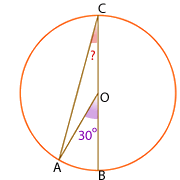
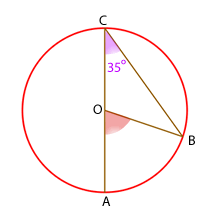
7Calcular el valor del ángulo que falta en cada una de las circunferencias siguientes

º

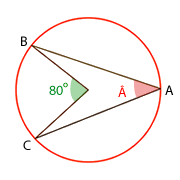
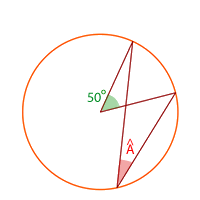
8. Calcula los ángulos inscritos de las siguientes figuras

º

º
