MATE 3. Semana del 20 al 24 de enero 2020
|
Bloque:
|
2
|
|
Eje:
|
Forma, espacio y medida.
|
|
TEMA:
|
Figuras
y cuerpos
|
|
Contenido:
|
•
Resolución de problemas geométricos mediante el teorema de Tales.
|
|
APRENDIZAJES
ESPERADOS
|
•
Construye polígonos semejantes. Determina y usa criterios de semejanza de
triángulos.
|
El teorema de Tales
Tenemos dos rectas secantes (que no son paralelas). A una la llamaremos la recta r (color rojo) y a la otra la llamaremos la recta s (color azul):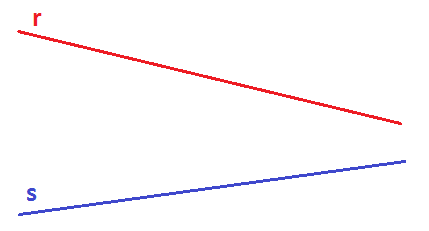
A estas dos rectas, las cortamos con varias rectas paralelas (color verde), de la siguiente manera:
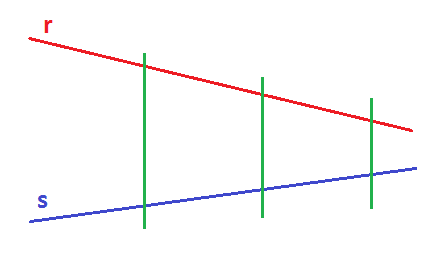
A los puntos donde cortan las rectas paralelas a la recta r, los voy a llamar A, B y C y a los puntos donde cortan las rectas paralelas a la recta s, los llamaré A’, B’ y C’:

Las rectas verdes, han dividido a la recta r en dos segmentos: el segmento AB y el segmento BC. Además tenemos un tercer segmento si consideramos la primera y la última recta paralela, es decir, el segmento AC.
También han dividido a la recta s en dos segmentos A’B’ y B’C’ y si consideramos la primera y la última recta paralela, existe un tercer segmento A’C’.
El teorema de Tales nos dice lo siguiente:
Cuando dos rectas cualesquiera, r y s, son cortadas por varias rectas paralelas, los segmentos que forman la recta r son proporcionales a los segmentos que forman la recta s.
¿Y eso que quiere decir?
Pues que si divides las longitudes de los segmentos que están enfrentados, es decir, el segmento AB entre el segmento A’B’ tienen la misma razón que si divides el segmento BC entre el segmento B’C’:

Como tienen la misma razón, AB y A’B’ son proporcionales a BC y B’C’.
Si consideramos el segmento formado por la primera y la última recta paralela, es decir, el segmento AC, también es proporcional al segmento AB:
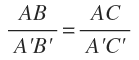
Y por tanto, todos los segmentos de la recta r son proporcionales a los segmentos de la recta s:
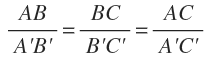
¿Para qué sirve el teorema de Tales?
El teorema de Tales te permite calcular la longitud de un segmento, conocidos los valores de todos los demás segmentos de dos rectas que se encuentran en posición de Tales.
Encontrarse en posición de Tales significa que las rectas tienen que estar tal y como dice el teorema de Tales, es decir, dos rectas secantes cortadas por varias rectas paralelas.
También podemos dividir un segmento en partes iguales, como veremos a continuación:
Como dividir un segmento en partes iguales con el teorema de Tales
Vamos a ver cómo dividir un segmento cualquiera en partes iguales aplicando el teorema de Tales.
Ejemplo de división de un segmento en partes iguales con el teorema de Tales
Podemos utilizar el teorema de Tales para dividir un segmento cualquiera en partes iguales, independientemente de la longitud del segmento.
¿Cómo utilizamos el teorema de Tales para dividir un segmento cualquiera?
Vamos a verlo paso a paso.
Tenemos un segmento cualquiera:

Podemos dibujar una semirrecta, que tenga una dirección cualquiera, a partir de uno de los extremos del segmento.
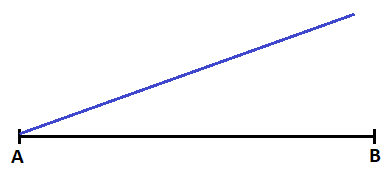
Esa semirrecta la vamos colocando una medida cualquiera, de una longitud que conocemos, de por ejemplo de 1 cm, de 2 cm o de lo que queramos, ayudándonos de una regla. El número de veces que vamos añadiendo la medida conocida sobre la semirrecta tiene que coincidir con el número de partes en la que se quiera dividir el segmento.
Por ejemplo, voy a dividir la semirrecta en 4 partes de 1 cm cada una. La voy añadiendo una a continuación de la otra:
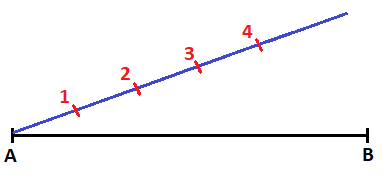
La última división, la unimos con el extremo B del segmento:

Finalmente, trazamos líneas paralelas a la recta 4-B, que pasen por las divisiones de la semirrecta 3, 2 y 1 y que corten al segmento AB:

El segmento AB queda dividido por tanto en 4 partes iguales y cada una de esas partes son proporcionales a las partes de la semirrecta. Ahí es donde se cumple el teorema de Tales y el cual lo hemos aprovechado para hacer esto.
Como ves, no necesitamos conocer la longitud del segmento AB para dividirlo. Por tanto, el teorema de Tales es muy útil para dividir segmentos cuya longitud no conocemos o que no podemos dividir directamente, ya que la división entre la longitud total del segmento y el número de partes no es exacta.
Podemos dividir el segmento AB en el número de partes que queramos, tan solo añadiendo más medidas a la semirrecta. Por otro lado, la semirrecta puede partir desde el punto A o desde el punto B del segmento indiferentemente y puede tener cualquier dirección, es decir, podría ser incluso perpendicular al segmento.
Ejercicio 1
Las rectas a y b del dibujo son paralelas. Comprueba utilizando el teorema de Tales si también lo es la recta c.

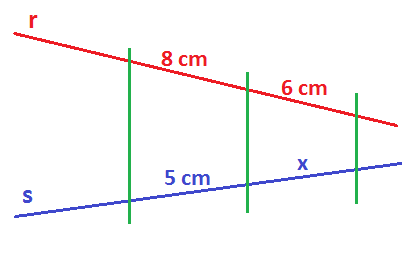
Ejercicio 2
¿Cuánto mide el segmento x en este dibujo?
4. Cuenta la leyenda que Tales para medir la altura de la pirámide de Keops colocó un palo de un metro en el centro de una circunferencia de radio 1m y esperó hasta que la sombra midiese exactamente un metro, instante en el que la sombra de la pirámide media 147 m¿ cuánto mide de alto la pirámide?
5. Calcula la altura de un edificio sabiendo que en un determinado momento del día proyecta una sombra de 6 metros, y una persona que mide 1,8 m. tiene, en ese mismo instante, una sombra de 70 cm.
6. Sergio sale en una foto con su amigo Enrique . en la foto Sergio mide 4,5 cm y Enrique 4,25cm . Si en la realidad Enrique mide 1,7 metros,¿Cuánto mide Sergio?
7. Halla la altura de un árbol sabiendo que su sombra mide 12 metros y que en ese mismo instante la sombra de una varilla de 1,5 metros mide 4,5 metros
8.Las rectas a, b y c son paralelas. Halla la longitud de x.
9. Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?
Hallar las medidas de los segmentos a y b.
10. Los siguientes triángulos están en posición de Tales. Calcula las longitudes
e

11. Las sombras de cuatro árboles miden, a las cinco de la tarde, 12 metros, 8 metros, 6 metros y 4 metros, respectivamente. El árbol pequeño tienen una altura de de 2,5 metros. ¿Qué altura tienen los demás?
12. ¿Cuál es la distancia entre el chico y la base de la torre (el chico ve la torre reflejada en el agua)?


Ejercicio 14
Calcula la altura de un edificio que proyecta una sombra de 49 metros en el momento en que un poste de 2 metros arroja una sombra de 1,25 metros.
Ejercicio 15
Las sombras de cuatro árboles miden, a las cinco de la tarde, 12 metros, 8 metros, 6 metros y 4 metros, respectivamente. El árbol pequeño tienen una altura de de 2,5 metros. ¿Qué altura tienen los demás?
Ejercicio 16
¿A qué altura se encuentra el extremo superior de la escultura, sabiendo que Paula la ve alineada con el borde de la valla?

17. Sabiendo que las rectas r, s y t son paralelas, la longitud de x es


6 Sean a y b dos rectas cualesquiera y r y s dos rectas que las cortan.
Si los segmentos que determinan a y b son m = 5.5, n = 4, m' = 2.5 y n' = 2 entonces...
Si los segmentos que determinan a y b son m = 5.5, n = 4, m' = 2.5 y n' = 2 entonces...
7 Sabiendo que el segmento DE es paralelo a la base del triángulo, las medidas
de los segmentos a y b son...
de los segmentos a y b son...

8 Sabiendo que los segmentos que miden 3 cm y 4 cm son paralelos, calcular a y b.

TEOREMA DE THALES
TEOREMA DE TALES
Si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.
El teorema de Thales en un triángulo
Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.






