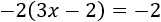MATE 2. Semana del 20 al 24 enero 2020


BLOQUE
2
EJE:
Número, álgebra y variación
TEMA:
Ecuaciones
SECUENCIA:
12. Sistemas de ecuaciones lineales con dos incógnitas
LECCIÓN:
1. Ecuaciones lineales
APRENDIZAJES ESPERADOS:
• Resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.





ECUACION LINEAL
En la ciencia de la matemática, se llama ecuación a aquella igualdad la cual tiene como mínimo una incógnita, dado que puede haber más, la cual deberá ser descubierta para dar con la solución.
ELEMENTOS:
  • Los miembros: son cada una de las expresiones algebraic as (valores).
  • Incógnitas: es aquel valor o los valores a descubrir, las cuales se expresaran a través de diferentes operaciones matemáticas.
Los valores conocidos que se enuncian en una ecuación pueden consistir en números, variables, constantes o coeficientes, mientras que los valores desconocidos o incógnitas serán simbolizados a partir de letras que hacen las veces del valor que más tarde se conocerá.
Ejemplo:
5 + X = 10
Es una ecuación simple, donde los números 5 y 10 son los valores que conocemos y X el que desconocemos y hay que averiguar.
Resolución:
X = 10 – 5
Por lo que X = 5. La incógnita de la ecuación es 5.
EJEMPLO

 Ecuación 1
Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.

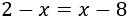
Para resolver la ecuación, debemos pasar los monomios que tienen la incógnita a una lado de la igualdad y los que no tienen la incógnita al otro lado.
Como 8 está restando en la derecha, pasa sumando al lado izquierdo:
Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.
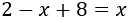Como x está restando en la izquierda, pasa restando a la derecha:
Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.
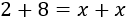Ahora que ya tenemos separados los monomios con y sin la incógnita, podemos sumarlos. En la izquierda, sumamos 2+8 y, en la derecha, x+x:
Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.
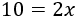Para ver con claridad el paso siguiente, escribimos 2x como un producto:
Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.
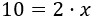Para terminar, debemos pasar el coeficiente de la incógnita (el número 2 que multiplica a x) al lado izquierdo. Como el número 2 está multiplicando, pasa dividiendo:
Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.
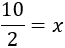Simplificando la fracción,
Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.
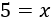Por tanto, la solución de la ecuación es x=5. Para comprobar la solución, sustituimos x por 5 en la ecuación:
Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.
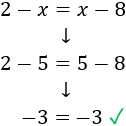Como hemos obtenido una igualdad verdadera (-3 es igual a -3), la solución es correcta. Si, por el contrario obtenemos una igualdad falsa, significa que hemos cometido algún error en la resolución de la ecuación.


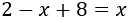
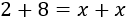
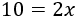
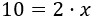
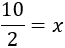
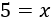
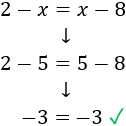
EJERCICIOS

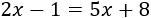
1. Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.

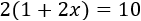
2. Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.

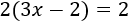
3. Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.

4. Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.























Entradas populares de este blog

MATE 1. Semana del 25 al 29 mayo 2020

Imagen
BLOQUE: 3 EJE: Forma, espacio y medida TEMA: Magnitudes y medidas SUBTEMA: 31. Volumen de prismas      APRENDIZAJES ESPERADOS: • Calcula el volumen de prismas rectos cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando fórmulas. Empecemos por recordar los elementos de un polígono regular. Para calcular el área de los polígonos regulares se necesita conocer su apotema. Recordemos que el área viene dada por la fórmula    Te  anexo un formulario para calcular el área  y el perímetro de varios polígonos regulares que te pueden ser de utilidad para que a su vez puedas calcular el volumen de prismas, por si no te acuerdas. Ejemplo 1. Calcula el volumen de un prisma con base rectangular, la cuál tiene de base 8cm y de altura 5cm. Sabemos que h=10 cm Dibujo             ...
Leer más

MATE 2. SEMANA DEL 18 AL 22 MAYO 2020

Imagen
BLOQUE: 3 EJE: FORMA, ESPACIO Y MEDIDA TEMA: • Magnitudes y medidas SECUENCIA: 21. Volumen de prismas rectos LECCIÓN: 1. Volumen de prismas rectos con base en forma de polígonos regulares APRENDIZAJES ESPERADOS: • Calcula el volumen de prismas y cilindros rectos. El prisma Los prismas son poliedros que tienen: Está constituido por dos bases poligonales e iguales y sus caras laterales son paralelogramos. Según el  número de lados de la base se le da el nombre al prisma. Por ejemplo:   Prismas triangular (sus bases son un triángulo), Prismas cuadrangulares (sus bases son cuadrados), Prisma pentagonal (sus bases son pentágonos), Prisma hexagonal (sus bases son hexágonos) , etc. La altura de un prisma es la distancia entre las bases.  Ejemplo y fórmula volumen de un prisma recto Un  prisma recto   tiene como bases d...
Leer más

MATE 2. Semana del 11 al 15 marzo 2019

Imagen
BLOQUE III EJE: Forma, espacio y medida TEMA: Figuras y cuerpos Subtema • Formulación de una regla que permita calcular la suma de los ángulos interiores de cualquier polígono. APRENDIZAJES ESPERADOS:  • Justifica la suma de los ángulos internos de cualquier triángulo o polígono y utiliza esta propiedad en la resolución de problemas.                                                                                         SUMA DE ÁNGULOS INTERIORES DE UN POLÍGONO La suma...
Leer más