MATE 1. Semana del 13 al 17 enero 2020

BLOQUE:	2
EJE:	Número, álgebra y variación
TEMA:	Proporcionalidad
SUBTEMA:	15. Proporcionalidad directa
APRENDIZAJES                         ESPERADOS:	Calcula valores faltantes en problemas de proporcionalidad directa, con constante natural, fracción o decimal

Introducción

Proporcionalidad directa:
Dos magnitudes $a$ y $b$ son directamente proporcionales cuando existe una constante $k$ tal que

$$\frac{a}{b}=k$$

La constante $k$ se denomina constante de proporcionalidad o razón.
Se dice que $a$ y $b$ mantienen una relación de proporcionalidad directa.

En este tipo de proporcionalidad, cuando una de las magnitudes aumenta, la otra también; y lo mismo ocurre cuando alguna de las dos disminuye.

Ejemplo:
En un movimiento con velocidad constante $v$, la distancia recorrida viene dada por la ecuación

$$distancia=v\cdot tiempo$$

La distancia es directamente proporcional al tiempo puesto que

$$\frac{distancia}{tiempo}=v$$

En este ejemplo, la velocidad es la constante de proporcionalidad.
Cuando el tiempo aumenta, la distancia también lo hace y viceversa.

Regla de tres (directa)

Si dos magnitudes $a$ y $b$ mantienen una relación de proporcionalidad directa, una regla de tres simple directa (o simplemente regla de tres directa) nos permite conocer el valor de una de las dos magnitudes cuando la otra varía.

Para aplicar una regla de tres, escribimos la siguiente tabla:

+	Valor	Valor
Magnitud $a$	$a_1$	$a_2$
Magnitud $b$	$b_1$	$b_2$

Como la relación de proporcionalidad directa debe ser constante, ha de cumplirse que

$$\frac{a_1}{b_1}=\frac{a_2}{b_2}$$

De esta relación podemos despejar el valor que deseamos calcular.

EJERCICIOS

La siguiente tabla muestra la altura de una planta correspondiente a diferentes edades.

Edad (en semanas)	$3$3	$7$7	$10$10
Altura (en centímetros)	$12$12	$35$35	$60$60

¿La altura de la planta es proporcional a su edad?

Escoge 1 respuesta:

Escoge 1 respuesta:

• Sí
• No

Anna hace abdominales para estar lista para su primer triatlón. Cuando empieza, hace una abdominal cada $2$2 segundos, pero conforme se cansa, cada abdominal le lleva más tiempo.

¿El número de abdominales que hace Anna es proporcional al tiempo que le toma hacerlos?

Escoge 1 respuesta:

Escoge 1 respuesta:

• Sí
• No

Estás preparando limonada. La cantidad de azúcar que necesitas depende de la cantidad de mezcla para limonada que uses.

Tazas de azúcar	$\dfrac13$start fraction, 1, divided by, 3, end fraction	$1$1	$3$3
Paquetes de mezcla para limonada	$1$1	$3$3	$9$9

¿La cantidad de azúcar que necesitas es proporcional a la cantidad de mezcla para limonada que usas?

Escoge 1 respuesta:

Escoge 1 respuesta:

• Sí
• No

En la gasolinera, cada litro de gasolina cuesta $\$3$dollar sign, 3. Sin embargo, hay una oferta: por cada bebida que compres, ahorras $\$0{,}20$dollar sign, 0, comma, 20 en gasolina.

¿Tus ahorros totales en gasolina son proporcionales al número de bebidas que compras?

Escoge 1 respuesta:

Escoge 1 respuesta:

• Sí
• No

La siguiente tabla muestra el tiempo que se tarda un elevador en alcanzar tres pisos diferentes de un rascacielos.

Número de piso	$4$4	$16$16	$64$64
Tiempo necesario (en minutos)	$0{,}25$0, comma, 25	$1$1	$4$4

Con base en esta tabla, ¿el número de piso es proporcional al tiempo necesario para que el elevador lo alcance?

Escoge 1 respuesta:

Escoge 1 respuesta:

• Sí
• No

Jack hizo palomitas de maíz, pero $3$3 de los $150$150 granos no estallaron.

Determina si cada uno de los siguientes lotes tiene la misma razón de granos no estallados a granos totales que el maíz de Jack.

	Misma razón de granos no estallados a granos totales que el maíz de Jack	Diferente razón de granos no estallados a granos totales que el maíz de Jack
$2$2 no estallados de $75$75 granos
$4$4 no estallados de $200$200 granos
$1$1 no estallado de $50$50 granos

La relación entre el número de horas de trabajo de un plomero y los honorarios que cobra es proporcional. La tarifa por $5$5 horas de trabajo es $\$350$dollar sign, 350.

¿Cuáles de las siguientes pueden ser combinaciones de horas de trabajo y honorarios que cobra el plomero?

Elige 3 respuestas:

Elige 3 respuestas:

• $3$3 horas y $\$270$dollar sign, 270
• $3{,}5$3, comma, 5 horas y $\$245$dollar sign, 245
• $6$6 horas y $\$420$dollar sign, 420
• $7{,}25$7, comma, 25 horas y $\$507{,}50$dollar sign, 507, comma, 50
• $8$8 horas y $\$490$

La tabla muestra una relación proporcional entre los mililitros $(\text{ml})$left parenthesis, start text, m, l, end text, right parenthesis de pintura roja y los mililitros de pintura amarilla que se requieren para hacer un cierto tono de pintura anaranjada.

Mezclas de pintura

Roja $(\text{ml})$left parenthesis, start text, m, l, end text, right parenthesis	Amarilla $(\text{ml})$left parenthesis, start text, m, l, end text, right parenthesis
$10{,}5$10, comma, 5	$28$28
$7{,}5$7, comma, 5	$20$20
$9$9	$24$24
?	?

Falta un renglón de valores en la tabla.

¿Cuáles de las siguientes mezclas de pintura pueden utilizarse como los valores faltantes en la tabla?

Elige 2 respuestas:

Elige 2 respuestas:

• $1{,}25\,\text{ml}$1, comma, 25, start text, m, l, end text Roja y $5\,\text{ml}$5, start text, m, l, end text Amarilla
• $1{,}5\,\text{ml}$1, comma, 5, start text, m, l, end text Roja y $4\,\text{ml}$4, start text, m, l, end text Amarilla
• $8\,\text{ml}$8, start text, m, l, end text Roja y $3\,\text{ml}$3, start text, m, l, end text Amarilla
• $7\,\text{ml}$7, start text, m, l, end text Roja y $16\,\text{ml}$16, start text, m, l, end text Amarilla
• $4{,}5\,\text{ml}$4, comma, 5, start text, m, l, end text Roja y $12\,\text{ml}$12, start text, m, l, end text Amarilla

La altura del triángulo A es $2{,}5\text{ cm}$2, comma, 5, start text, space, c, m, end text y su base es $1{,}6\text{ cm}$1, comma, 6, start text, space, c, m, end text. La altura y base del triángulo B son proporcionales a las del triángulo A.

¿Cuáles de las siguientes pueden ser la altura y base del triángulo B?

Elige 3 respuestas:

Elige 3 respuestas:

• Altura: $2{,}75\text{ cm}$2, comma, 75, start text, space, c, m, end text
  Base: $1{,}76\text{ cm}$1, comma, 76, start text, space, c, m, end text
• Altura: $9{,}25\text{ cm}$9, comma, 25, start text, space, c, m, end text
  Base: $9{,}16\text{ cm}$9, comma, 16, start text, space, c, m, end text
• Altura: $3{,}2\text{ cm}$3, comma, 2, start text, space, c, m, end text
  Base: $5\text{ cm}$5, start text, space, c, m, end text
• Altura: $1{,}25\text{ cm}$1, comma, 25, start text, space, c, m, end text
  Base: $0{,}8\text{ cm}$0, comma, 8, start text, space, c, m, end text
• Altura: $2\text{ cm}$2, start text, space, c, m, end text
  Base: $1{,}28\text{ cm}$

Problema 1

Calcular la razón de los números

1. 15 y 25
2. 12 y 32
3. 3 y 81

Problema 2

Calcular el valor de la incógnita en cada una de las relaciones de proporcionalidad:

1		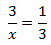2		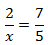3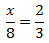
4		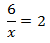5		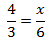6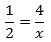
7		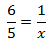8		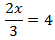9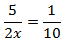

Problema 3

Completar la tabla para que las magnitudes de la primera fila sean directamente proporcionales a las de la segunda e indicar cuál es la constante de proporcionalidad.

Problema 4

Una empresa de refrescos dispone de 3 máquinas embotelladoras, que son suficientes para satisfacer un pedido diario de 2400 botellas. En verano el pedido diario asciende a 5600 botellas. Calcular cuántas máquinas embotelladoras han de alquilarse para asumir el incremento de la demanda.

Problema 5

El precio de un paquete de 13 rotuladores es de 9.75€. ¿Cuántos rotuladores podemos comprar con un presupuesto de 15.75€?

Problema 6

José marca 5 goles cada 25 minutos de partido. Calcular mediante una regla de tres cuántos goles marcará en una hora. Indicar si es una proporcionalidad directa o inversa.

Problema 7

El precio por kilo de queso azul es de 23.35€. ¿Cuánto nos costarán 125g de queso? Indicar si es una proporcionalidad directa o inversa.

Problema 8

Un autobús recorre 70km en dos horas. ¿Cuánto tardará en realizar un viaje de 345km? Indicar si es una proporcionalidad directa o inversa.

Problema 9

La puntuación de Sandra (sobre 10) en un examen de matemáticas de 39 preguntas es 3.3333... puntos. ¿Cuántas preguntas ha contestado correctamente?

Problema 10

Para obtener el certificado de inglés se necesita obtener un 7 sobre 10 en un test de 243 preguntas. Calcular el número mínimo de preguntas correctas necesarias para obtenerlo.