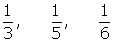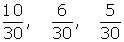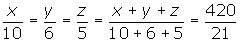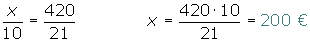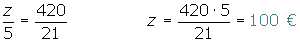MATE 2. Semana del 13 al 17 enero 2020
|
BLOQUE
|
2 |
|
EJE:
|
Número,
álgebra y variación
|
|
TEMA:
|
Proporcionalidad
|
|
SECUENCIA:
|
11.
Reparto proporcional
|
|
LECCIÓN:
|
1.
Situaciones de reparto proporcional
|
|
APRENDIZAJES
ESPERADOS:
|
Resuelve
problemas de proporcionalidad directa e inversa y de reparto proporcional.
|
Repartos directamente proporcionales
Consiste en que dadas unas magnitudes de un mismo tipo y una magnitud total, calcular la parte correspondiente a cada una de las magnitudes dadas.
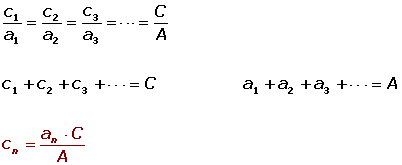
Ejemplo
Un abuelo reparte 450 € entre sus tres nietos de 8, 12 y 16 años de edad; proporcionalmente a sus edades. ¿Cuánto corresponde a cada uno?
Llamamos x, y, z a las cantidades que le corresponde a cada uno.
1º El reparto proporcional es:
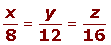
2º Por la propiedad de las razones iguales:
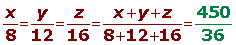
3º Cada nieto recibirá:
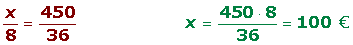
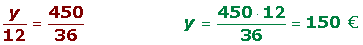
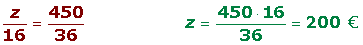
Repartos inversamente proporcionales
Dadas unas magnitudes de un mismo tipo y una magnitud total, debemos hacer un reparto directamente proporcional a las inversas de las magnitudes.
Ejemplo
Tres hermanos ayudan al mantenimiento familiar entregando anualmente 5900 €. Si sus edades son de 20, 24 y 32 años y las aportaciones son inversamente proporcionales a la edad, ¿cuánto aporta cada uno?
1º Tomamos los inversos:
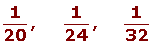
2º Ponemos a común denominador:

3º Realizamos un reparto directamente proporcional a los numeradores: 24, 20 y 15.
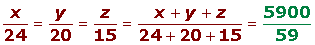
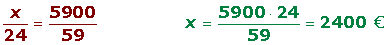
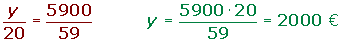
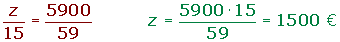
Ejercicios de ejemplo
Se asocian tres individuos aportando 5000, 7500 y 9000 €. Al cabo de un año han ganado 6 450 €. ¿Qué cantidad corresponde a cada uno si hacen un reparto directamente proporcional a los capitales aportados?
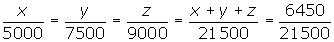
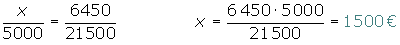
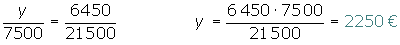
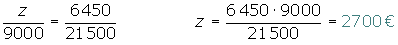
Repartir 420 €, entre tres niños en partes inversamente proporcionales a sus edades, que son 3, 5 y 6.