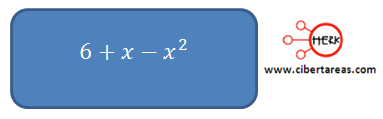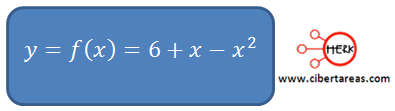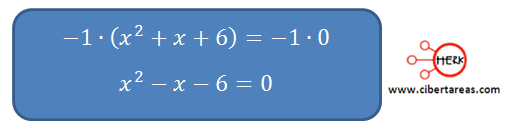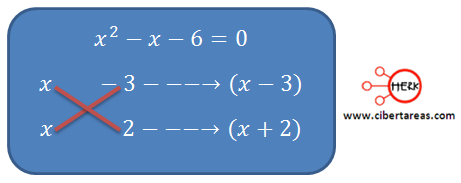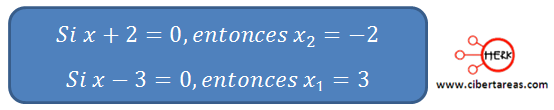MATE 3. Semana del 5 al 8 febrero 2019

Bloque:	3
Eje:	Análisis de la información
TEMA:	Proporcionalidad y funciones
SUBTEMA	• Lectura y construcción de gráficas de funciones cuadráticas para modelar diversas situaciones o fenómenos.
APRENDIZAJES ESPERADOS	• Resuelve problemas que implican el uso de ecuaciones de segundo grado.

Método Gráfico  para la solución de ecuaciones de segundo grado – Matemáticas 1

Como sabemos, existe un método grafico para solucionar una ecuación de primer grado y también existe un método grafico para solucionar ecuaciones de segundo grado, vamos a analizar un ejemplo en el cual veremos el comportamiento de las gráficas para las ecuaciones cuadráticas.

Tenemos el siguiente ejemplo:

Una base militar está ubicada en la coordenada (-3, -6), el militar de guardia localiza un tanque de guerra enemigo en la coordenada (3,0), el general ordena enviar un misil que describe una trayectoria definida por la siguiente ecuación de segundo grado:

Vamos a realizar la trayectoria del misil y determinar si el tanque enemigo será destruido por el misil.

Tenemos los siguientes datos:

La base militar está ubicada en la coordenada (-3, -6)

El tanque enemigo está ubicado en la coordenada (3, 0)

La función de la trayectoria que el misil sigue es: 6 + x – x2

Para graficar la trayectoria que seguirá el misil, es necesario establecer una relación funcional, en otras palabras:

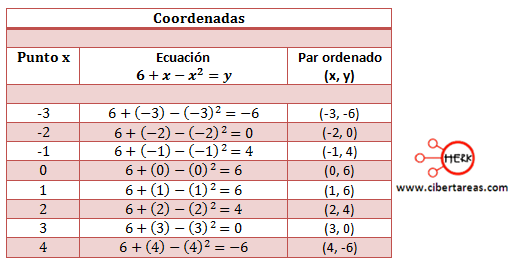
De esta manera se obtendrá la trayectoria del misil en cada coordenada (x, y) de su dominio, vamos a definir un dominio arbitrario de x [3, 4] y con estos datos realizaremos una tabulación de dichos datos.

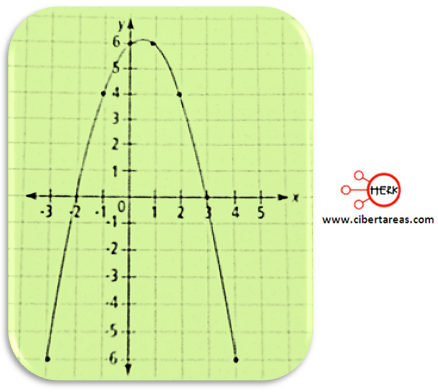
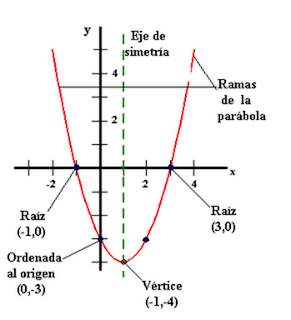
Al realizar la gráfica, tenemos como resultado una cóncava o parábola hacia abajo:

Tenemos que el misil lanzado describe una curva denominada parábola, se puede observar que la trayectoria para primero por el eje de las “x”, posteriormente alcanza un punto máximo y empieza a decrecer y vuelve a cruzar el eje de las “x”, en otras palabras alcanza su máximo en la coordenada (0, 6) del eje de las “y” y al decrecer para por la coordenada (3, 0) del eje “x”, en este punto es donde se localiza en tanque enemigo, con lo que se asegura el impacto del misil lanzado.

Podemos definir los dos puntos donde el misil corta el eje de las “x”, para esto, se necesita el método de factorización. Para resolver la ecuación por este proceso, se puede cambiar la forma de la ecuación:

Para este caso, la raíz cuadrada de –x2 no se puede extraer porque es negativa entonces se puede proponer una ecuación equivalente al multiplicar por -1 ambos miembros de la igualdad

Vamos a utiliza el método por inspección y multiplicamos en forma de cruz

Con esto podemos definir los dos valores de “x” por donde el misil pasa:

Recuerda los elementos que conforman la gráfica de una función cuadrática, la parábola

           

Cómo graficar una función cuadrática

Cuando se grafican, las ecuaciones cuadráticas de la forma ax² + bx + c  o  a(x - h)² + k, forman una curva en forma de U o U inversa llamada parábola. Graficar una ecuación cuadrática es cuestión de encontrar su vértice, dirección y por lo general sus interceptos en sus ejes (x, y). Si se trata de una ecuación cuadrática relativamente simple, podría ser suficiente crear una tabla con valores de x para trazar la curva con los puntos resultantes.

TAREA PARA ENTREGAR EL VIERNES 8 DE FEBRERO

1. Usa el siguiente plano coordenado para escribir los pares ordenados para cada punto.

$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{\llap{-}1}$$\small{\llap{-}2}$$\small{\llap{-}3}$$\small{\llap{-}4}$$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{\llap{-}1}$$\small{\llap{-}2}$$\small{\llap{-}3}$$\small{\llap{-}4}$$\green{A}$$\purple{B}$$\blue{C}$$y$$x$

A(    ,     )

B (    ,    )

C(    ,    )

2. ¿Para cuáles puntos la coordenada $y$ es menor que $-1.5$?

$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{\llap{-}1}$$\small{\llap{-}2}$$\small{\llap{-}3}$$\small{\llap{-}4}$$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{\llap{-}1}$$\small{\llap{-}2}$$\small{\llap{-}3}$$\small{\llap{-}4}$$\greenD{A}$$\purpleD{B}$$\blueD{C}$$\goldD{D}$$y$$x$

Elige todas las respuestas adecuadas:

Elige todas las respuestas adecuadas:

• 
  

  
  

  
  

  Punto $\greenD{A}$
• 
  

  
  

  
  

  Punto $\purpleD{B}$
• 
  

  
  

  
  

  Punto $\blueD{C}$
• 
  

  
  

  
  

  Punto $\goldD{D}$

Grafica las ecuaciones siguientes y encuentra:

a) el vértice

b) si abre hacia arriba o hacia abajo

c) las raíces de la ecuación

d) La ordenada al origen

$y=-2(x-1)^2-4$

$f(x)=2x^2-5$4. y=x2−2x+1

$$
y=2(x-4)^2+55.      y=x2+x−6

$f(x)=-(x+6)^2$

6.  f(x)=x²+3x+2

7.              x² – x -  2 = 0

8.            f(x)=x²+6x-7