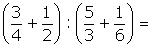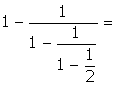MATE 2. Semana del 25 al 28 febrero 2019

BLOQUE	3
EJE:	Sentido numérico y pensamiento algebraico
TEMA:	Problemas multiplicativos
Subtema	• Resolución de cálculos numéricos que implican usar la jerarquía de las operaciones y los paréntesis, si fuera necesario, en problemas y cálculos con números enteros, decimales y fraccionarios
APRENDIZAJES ESPERADOS:	Resuelve problemas que implican efectuar multiplicaciones o divisiones con expresiones  algebraicas.

CÁLCULO DE UN POLINOMIO ARITMÉTICO Para calcular un polinomio aritmético, por ejemplo 5 - 2 - 4 + 7 - 3, se siguen estos pasos:
1.° Se suman los números que llevan signo +: 5 + 7 = 12.
2.° Se suman los números que llevan signo -: 2 + 4 + 3 = 9.
3.° Se resta del primero (12) el segundo (9): 12 - 9 = 3.

5 - 2 - 4 + 7 - 3 = (5 + 7) - (2 + 4 + 3) = 12 - 9 = 3

CÁLCULO CON PARÉNTESIS • Para suprimir un paréntesis precedido del signo +, se dejan los signos del interior del paréntesis como están.
Ejemplo: • 3 + 2 + (4 - 3 - 2) = 3 + 2 + 4 - 3 - 2 = (3 + 2 + 4) - (3 + 2) = 9 - 5 = 4

• Para suprimir un paréntesis precedido del signo -, se cambian todos los signos del interior del paréntesis. Ejemplo: 7 + 2 - (4 - 3 + 1 ) = 7 + 2 - 4 + 3 - 1 = 12 - 5 = 7

CÁLCULO CON CORCHETES Los corchetes [ ] se utilizan cuando en una expresión hay más de un paréntesis. Para calcular una expresión con corchetes, por ejemplo 3 - [6 - (-4 + 2) - 1], se siguen estos pasos:
 1.° Se suprimen los paréntesis: 3 - [6 - (-4 + 2) - 1] = 3 - [6 + 4 - 2 - 1]

2.° Se suprimen los corchetes y se calcula. 3 - [6 + 4 - 2 - 1] = 3 - 6 - 4 + 2 + 1 = (3 + 2 + 1) - (6 + 4) = -4

JERARQUIZACIÓN DE OPERACIONES

1º.Efectuar las operaciones entre paréntesis, corchetes y llaves.

2º.Calcular las potencias y raíces.

3º.Efectuar los productos y cocientes.

4º.Realizar las sumas y restas.

Tipos de operaciones combinadas

1. Operaciones combinadas sin paréntesis

1.1 Combinación de sumas y diferencias.

9 - 7 + 5 + 2 -6 + 8 - 4 =

Comenzando por la izquierda, vamos efectuando las operaciones según aparecen.

= 9 - 7 + 5 + 2 -6 + 8 - 4 = 7

1.2 Combinación de sumas, restas y productos.

3 · 2 - 5 + 4 · 3 - 8 + 5 · 2 =

Realizamos primero los productos por tener mayor prioridad.

= 6 - 5 + 12 - 8 + 10 =

Efectuamos las sumas y restas.

= 6 - 5 + 12 - 8 + 10 = 15

1.3 Combinación de sumas, restas, productos y divisiones.

10 : 2 + 5 · 3 + 4 - 5 · 2 - 8 + 4 · 2 - 16 : 4 =

Realizamos los productos y cocientes en el orden en el que los encontramos porque las dos operaciones tienen la misma prioridad.

= 5 + 15 + 4 - 10 - 8 + 8 - 4 =

Efectuamos las sumas y restas.

= 5 + 15 + 4 - 10 - 8 + 8 - 4 = 10

1.4 Combinación de sumas, restas, productos, divisiones y potencias.

2³ + 10 : 2 + 5 · 3 + 4 - 5 · 2 - 8 + 4 · 2² - 16 : 4 =

Realizamos en primer lugar las potencias por tener mayor prioridad.

= 8 + 10 : 2 + 5 · 3 + 4 - 5 · 2 - 8 + 4 · 4 - 16 : 4 =

Seguimos con los productos y cocientes.

= 8 + 5 + 15 + 4 - 10 - 8 + 16 - 4 =

Efectuamos las sumas y restas.

= 26

2. Operaciones combinadas con paréntesis

(15 - 4) + 3 - (12 - 5 · 2) + (5 + 16 : 4) -5 + (10 - 2³)=

Realizamos en primer lugar las operaciones contenidas en ellos.

= (15 - 4) + 3 - (12 - 10) + (5 + 4) - 5 + (10 - 8 )=

Quitamos paréntesis realizando las operaciones.

= 11 + 3 - 2 + 9 - 5 + 2 = 18

3.Operaciones combinadas con paréntesis y corchetes

[15 - (2³ - 10 : 2 )] · [5 + (3 ·2 - 4 )] - 3 + (8 - 2 · 3 ) =

Primero operamos con las potencias, productos y cocientes de los paréntesis.

= [15 - (8 - 5 )] · [5 + (6 - 4 )] - 3 + (8 - 6 ) =

Realizamos las sumas y restas de los paréntesis.

= [15 -3 ] · [5 + 2 ] - 3 + 2=

Operamos en los paréntesis.

= 12 · 7 - 3 + 2

Multiplicamos.

= 84 - 3 + 2=

Restamos y sumamos.

= 83

TAREA PARA ENTREGAR EL JUEVES 28 FEBRERO

• 5 − 3 − 2 · 2 =

• 3 - [2 + 4 - (2 - 7) + 1] - [2 - (4 + 7 - 1) - 2] = 

• -2 - 7 - [-3 + 1 - (1 + 2 - 3) + 1] - [-7 + 4 - (2 + 5)] = 

• [-9 - 11 - (-18 + 21 - 3) + 7] - [-18 + 21 - (3 - 11 + 15)] = 

• -4 - 12 - [(-13 - 20 + 8) - 4] - [-21 + 16 - (-15 + 3)] = 

•  −8 · [5 − (−2)] − 48 : [6 + (−14)] − 11 · [10 + (−7)] + 36 : [(−1) − (−10)] =
•  (5 + 3 · 2 : 6 − 4 ) · (4 : 2 − 3 + 6) : (7 − 8 : 2 − 2)² =
•  [(17 − 15)³ + (7 − 12)²] : [(6 − 7) · (12 − 23)] =

• 

• 

• 2{4 [7 + 4 (5 · 3 − 9)] − 3 (40 − 8)} = 

• 14 − {7 + 4 · 3 - [(-2)² · 2 - 6)]}+ (2² + 6 - 5 · 3) + 3 - (5 - 2³ : 2) =

REALIZA LA ACTIVIDAD DEL SIGUIENTE LINK. CÓPIALA EN TU CUADERNO.

http://www.juntadeandalucia.es/averroes/centros-tic/41009470/helvia/aula/archivos/repositorio/0/193/html/recursos/la/U01/pages/recursos/143304_P11/es_carcasa.html

TAREA PARA ENTREGAR EL JUEVES 28 FEBRERO

1. ¿En qué orden se deben efectuar los cálculos en las siguientes expresiones para obtener los resultados que se indican? Pongan paréntesis a los cálculos que se hacen primero.

a)    25 + 40 x 4 – 10 ¸ 2 = 180

b)    8 – 2 ÷ 3 + 4 x 5 = 22

c)    15 ÷ 3 – 7 – 2 = 0

d)    18 + 4 x 3 ÷ 3 x 2 = 26

      e)  21 – 14 ÷ 2 + 7 x 2 = 28

2. Jorge fue a comprar un par de cuadernos en una papelería que tenía la siguiente oferta:

	Todos los cuadernos de la marca x, 20 % de descuento.

 

El precio de un cuaderno, sin descuento, era de $25.00. El pagó con un billete de $100.00 y le dieron de cambio $60.00.

De acuerdo con esta información, ¿cuál de las siguientes operaciones representa la situación anterior?

a)  100-2 x 25-50 x 20/100 =

b)  100-((2 x 25)-(50 x 20/100)) =

c)  100+(2 x 25)+(50 x 20/100) =

d)  (100-(2 x 25))-(50 x 20/100) =

3. Un terreno tiene la siguiente forma:

 

a)    ¿Cuál es la expresión algebraica que representa el área del terreno?

b)    Si el valor de n es 6 metros, ¿cuántos metros cuadrados tiene el terreno?

c)    ¿Cuál es el perímetro del terreno?

 4 - [2 - (-3 + 5) - 8] = 4 - [2 + 3 - 5 - 8] = 4 - 2 - 3 + 5 + 8 = = (4 + 5 + 8) - (2 + 3) = 17 - 5 = 12