MATE 3. Semana del 11 al 15 de febrero 2019
|
Bloque:
|
3
|
|
Eje:
|
Análisis de la información
|
|
TEMA:
|
Nociones de Probabilidad
|
|
SUBTEMA
|
• Cálculo de la probabilidad de ocurrencia de dos eventos
independientes (regla del producto).
|
|
APRENDIZAJES ESPERADOS
|
• Resuelve problemas de congruencia y semejanza que implican utilizar
estas propiedades en triángulos o en cualquier figura.
• Resuelve problemas que implican el uso de ecuaciones de segundo grado. |
Regla del producto en Probabilidad para eventos independientes
Definiciones
Eventos independientes
Dos eventos son independientes si el resultado del segundo evento no es afectado por el resultado del primer evento.
Es decir, son aquellos eventos cuyo resultado no tienen que ver con el resultado de otro(s) evento(s).
Por ejemplo, el resultado de lanzar una moneda, y que caiga de cualquier lado, no depende del resultado de ninguno de los lanzamientos anteriores. Por lo tanto, cada lanzamiento es un evento independiente
Regla del producto:
Por lo anterior, Si A y B son eventos independientes, la probabilidad de que ambos eventos ocurran es el producto de las probabilidades de los eventos individuales.
P(A y B) = P(A) · P(B)
Ejemplo 1:
Una caja contiene 4 canicas rojas, 3 canicas verdes y 2 canicas azules. Una canica es eliminada de la caja y luego reemplazada. Otra canica se saca de la caja.
¿Cuál es la probabilidad de que la primera canica sea azul y la segunda canica sea verde?
Solución:
Ya que la primera canica es reemplazada (es decir se saca y se vuelve a meter la misma canica u otra del mismo color), el tamaño del espacio muestral (9) no cambia de la primera sacada a la segunda, así los eventos son independientes.
P(azul luego verde) = P(azul) · P(verde)

Otros ejemplos ilustrativos
1) De una baraja estándar de 52 cartas sea A el suceso de sacar un As en la primera extracción y B sacar un Rey en la segunda extracción. Calcular la probabilidad de sacar un As y un Rey en dos extracciones devolviendo la carta extraída.
Solución:
A y B son sucesos independientes porque la ocurrencia de A afecta la probabilidad de ocurrencia de B.
La probabilidad de que la primera carta sea un As es:

Reemplazando los anteriores valores en la regla particular de la multiplicación se obtiene:
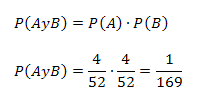
2) Una pareja de esposos desean tener 3 hijos. Suponiendo que las probabilidades de tener un niño o una niña son iguales, calcular la probabilidad de éxito en tener hombre en el primer nacimiento, mujer en el segundo nacimiento y hombre en el tercer nacimiento.
Solución:
M = mujer
H = hombre
Elaborando un diagrama de árbol se tiene todas las probabilidades:
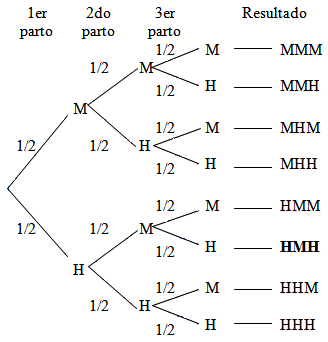
Entonces,
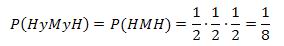
Para comprobar si o no dos sucesos A y B son independientes, calcule P(A), P(B), and P(A ∩ B), y entonces comprobar si P(A ∩ B) es igual a P(A)P(B). Si son iguales, entonces A y B son independientes; si no, son dependientes.
1. En una fábrica de zapatos se manufactura independientemente costura, suela y tacón. Siendo estas partes armadas aleatoriamente en cada zapato. Se sabe que en este proceso, el 5% de las costuras, el 4% de las suelas y el 1% de los tacones tienen fallas. Si se toma un zapato terminado calcular la probabilidad:
a) Que tenga fallas en sus 3 componentes
b) Que tenga fallas en la costura y el tacón
c) Sin fallas en sus 3 componentes
2. Se lanza un dado dos veces. ¿Cual es la probabilidad de que en el primer lanzamiento resulte 3 y en el segundo lanzamiento un numero impar?
3. Un estudiante responde al azar 5 preguntas de verdadero y falso en un examen. ¿Cuál es la probabilidad de que acierte todas las preguntas?
4. Un alumno contesta al azar 70 preguntas de un examen, si cada pregunta tiene 5 alternativas y solo una de ellas es correcta. ¿cual es la probabilidad de que saque el puntaje máximo?
5. Un restaurante ofrece un almuerzo en que se pueden elegir 2 entradas, 3 platos de fondo y 5 postres.
Si no me gustan 2 de los platos de fondo y 3 de los postres. ¿Cuál es la probabilidad de que me toque un menú de mi agrado si la elección es al azar?
6. En una empresa trabajan hombres y mujeres, ademas se sabe que un 15% de los empleados se han perfeccionado en el extranjero. Si el 35% de las son mujeres, ¿cual es la probabilidad de que al escoger una persona de la empresa, esta sea mujer y se haya perfeccionado en el extranjero?Si no me gustan 2 de los platos de fondo y 3 de los postres. ¿Cuál es la probabilidad de que me toque un menú de mi agrado si la elección es al azar?
7. Tiras dos dados; uno verde y uno rojo, y observas los números orientados hacia arriba. Tomas A: la suma es 7, and B: el dado rojo sale par . ¿Son estos dos sucesos independientes?
