Mate 1. Semana del 5 al 8 febrero 2019.

BLOQUE :	2
EJE:	Número, álgebra y variación
TEMA:	Proporcionalidad
SUBTEMAS:	16. Problemas de porcentajes
APRENDIZAJES ESPERADOS	Resuelve problemas de cálculo de porcentajes, de tanto por ciento y de la cantidad base.

Porcentajes

%

1. Definición y EJEMPLOS

Un porcentaje es una proporción tomando como referencia el número 100.
Se expresa con un número entre 0 y 100 seguido del símbolo %.

Ejemplos:

• El 50% es la mitad ya que 50 es la mitad de 100.
  El 50% de 200 es 100.
  
  

2. Cálculo de Porcentajes

Métodos para obtener el tanto por ciento (porcentaje) de una determinada cantidad.
Veremos dos métodos para calcular porcentajes: aplicar una regla de tres o multiplicar por un decimal.
En realidad, el segundo de los métodos es el mismo que el primero: se aplica una regla de tres, pero multiplicando directamente por un número decimal.

Método 1: Regla de tres

Los porcentajes son siempre relaciones de proporcionalidad directa.
Identificaremos el total con el 100% para obtener los porcentajes.

Ejemplo:
Vamos a calcular el 25% de 324.
Como 324 es el total, lo identificamos con el 100%:

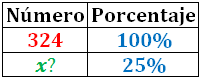Aplicando la regla de tres, podemos calcular el valor de la incógnita x que representa el 25% de 324:

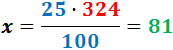
Por tanto, el 25% de 324 es 81.

Método 2: Multiplicar por un Decimal

En realidad este método es calcular una regla de tres, pero de forma más rápida (omitiendo operaciones).
Como hemos visto, para calcular el tanto por ciento de una cantidad multiplicamos dicha cantidad por el número del porcentaje y dividimos por 100.
Estas dos operaciones podemos realizarlas directamente multiplicando por un decimal.

Ejemplo:

• Calculamos el 35% de 80
  Solo tenemos que multiplicar 80 por el decimal 0,35 (0,35 es 35 dividido entre 100):
  
  

4. Tanto por ciento mayor que 100%

También podemos calcular porcentajes mayores que 100.
El procedimiento es el mismo.

Ejemplo: Vamos a calcular el 150% de 30 aplicando una regla de tres:
Como 30 es el total, lo identificamos con el 100%:

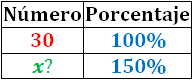Calculamos la incógnita x:

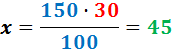Por tanto, el 150% de 30 es 45.

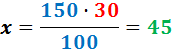
5. Rebajas y Descuentos

Es muy frecuente emplear porcentajes para expresar disminuciones o decrecimientos. Lo vemos todos los años en las rebajas de las tiendas.
Si un precio está rebajado, por ejemplo, un 40%, quiere decir que el precio actual es el precio inicial menos su 40%. Esto es, el precio actual es el 60% del precio inicial ya que al 100% le hemos quitado el 40%:

Generalmente, para expresar que aplicamos un descuento (una rebaja), se escribe el signo negativo delante del tanto por ciento.
Siguiendo con el mismo ejemplo, veríamos en la tienda:

Por tanto, si queremos calcular el precio después del descuento, la forma más rápida es calcular el porcentaje que vamos a pagar. En el ejemplo, calculamos el 60%.
Si lo que queremos saber es cuánto ha bajado el precio, es decir, cuánto dinero estamos ahorrando, entonces calculamos el porcentaje rebajado. En el ejemplo, calculamos el 40%.

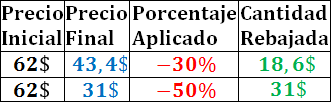
Ejemplo: En un artículo de 62$ rebajado un 30%

6. Aumentos o incrementos

Del mismo modo que empleamos los porcentajes para expresar descensos, también podemos emplearlos para expresar aumentos.

Ejemplo:
el salario de un trabajador es de 800$ y se le aplica un aumento del 20%.
Esto quiere decir que al salario inicial le hemos sumado el 20%.
El 20% de 800$ es

Por tanto, el salario actual es

TAREA PARA ENTREGAR EL VIERNES 8 DE FEBRERO
Recuerda la tarea consiste en a) copiar en tu cuaderno el apunte  anterior y b) la resolución de los ejercicios siguientes

1. ¿Cuánto es $40\%$ de $10$?

2. 24 es el $75\%$ de este número:75%

3. ¿Qué porcentaje es $162$ de $200$?162

4. ¿Cuánto es $2\%$ de $50$?$162$5. $12$ es el $60\%$ de este número:

RESUELVE LOS SIGUIENTES PROBLEMAS.

 1De los 800 alumnos de un colegio, han ido de viaje 600. ¿Qué porcentaje de alumnos ha ido de viaje? 

2Al adquirir un vehículo cuyo precio es de 8800 €, nos hacen un descuento del 7.5%. ¿Cuánto hay que pagar por el vehículo?

3El precio de un ordenador es de 1200 € sin IVA. ¿Cuánto hay que pagar por él si el IVA es del 16%? 

4Al comprar un monitor que cuesta 450 € nos hacen un descuento del 8%. ¿Cuánto tenemos que pagar?

5Se vende un artículo con una ganancia del 15% sobre el precio de costo. Si se ha comprado en 80 €. Halla el precio de venta.

6 Cuál será el precio que hemos de marcar en un artículo cuya compra ha ascendido a 180 € para ganar al venderlo el 10%.

7¿Qué precio de venta hemos de poner a un artículo comparado a 280 €, para perder el 12% sobre el precio de venta?

8Se vende un objeto perdiendo el 20% sobre el precio de compra. Hallar el precio de venta del citado artículo cuyo valor de compra fue de 150 €.

9. El 75% de una cantidad representa...

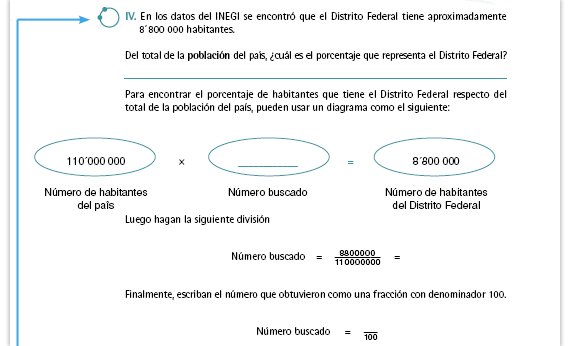
	La tercera parte.
	La cuarta parte.
	Tres cuartas partes.

10. El 25% del 50% de una cantidad es...

	La quinta parte de la mitad de dicha cantidad.
	La sexta parte de dicha cantidad.
	La mitad de la cuarta parte de dicha cantidad.

11. Si el precio de un artículo se rebaja en un 35%, entonces...

	Pagaremos sólo el 35% del precio inicial.
	Pagaremos sólo el 65% del precio inicial.
	Pagaremos sólo el 135% del precio inicial.

12.


13.