MATE 2. Semana del 5 al 9 noviembre 2018
Número, álgebra
y variación
Resolución de problemas diversos relacionados con el porcentaje, como aplicar un porcentaje a una cantidad; determinar qué porcentaje representa una cantidad respecto a otra, y obtener una cantidad conociendo una parte de ella y el porcentaje que representa.
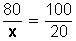
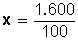
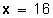
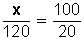
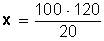
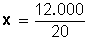
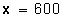
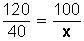
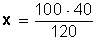

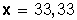

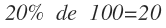
2. Para ir del pueblito de Santiago al de San Marcos, existen dos caminos. El tiempo de recorrido para el primer trayecto es de 2 horas y 15 minutos; el del segundo es de 1 hora y 45 minutos.
a) ¿Qué porcentaje representa la duración del trayecto por el segundo camino respecto a la duración del segundo?
b) ¿Qué porcentaje representa la duración del trayecto por el segundo camino respecto a la duración del primero?
3. El costo de una casa hace 7 años erade $350,000, hoy es de $720,000.
a) ¿En qué porcentaje se incrementa su valor?
b) ¿Cuántas veces se incrementa el valor de un objeto, si decimos que su precio aumentó 100%?
c) ¿Cuántas veces se incrementa el valor de un objeto, si decimos que su precio aumentó 200%?
4. En el municipio de Santa Camila han sido vacunados contra la demencia 336 niños y ellos representan el 60% de la población infantil.
a) ¿Cuál es la población infantil en el municipio?
b? ¿Cuántos niños faltan por vacunar?
5. Esta quincena Lissette ahorró $3200, si esa cantidad representa 46% de su sueldo. ¿Cuál es su sueldo quincenal?
6. De los 800 alumnos de un colegio, han ido de viaje 600. ¿Qué porcentaje de alumnos ha ido de viaje?
7. Al adquirir un vehículo cuyo precio es de 8800 dólares, nos hacen un descuento del 7.5%. ¿Cuánto hay que pagar por el vehículo?
8. El precio de un ordenador es de 1200 dólares sin IVA. ¿Cuánto hay que pagar por él si el IVA es del 16%?
9. Se vende un objeto perdiendo el 20% sobre el precio de compra debido a la devaluación. Hallar el precio de venta del citado artículo cuyo valor de compra fue de 150 dólares.
Resolución de problemas diversos relacionados con el porcentaje, como aplicar un porcentaje a una cantidad; determinar qué porcentaje representa una cantidad respecto a otra, y obtener una cantidad conociendo una parte de ella y el porcentaje que representa.
1.- Dada una cantidad total, calcular el número que corresponde a ese porcentaje (%) parcial :
Ejemplo: ¿Cuál (cuanto) es el 20% de 80?
Cantidad
|
Porcentaje
| |
Total
|
80
|
100
|
Parcial
|
x
|
20
|
Para resolverlo, se hace:
Haciendo la operación, queda:
Simplificando, queda:
Respuesta: el 20 % de 80 es 16.
2.- Calcular el total, dada una cantidad que corresponde a un porcentaje de él.
Ejemplo: Si el 20 % de una cierta cantidad total es 120 ¿Cuál es el total?
Cantidad
|
Porcentaje
|
x
|
100
|
120
|
20
|
Para resolverlo, se hace:
Resolvemos la incógnita (x):
Haciendo la operación, queda:
Simplificando, queda:
Respuesta: 120 es el 20 % de un total de 600.
3.- Dado el total y una parte de él calcular que % es esa parte del total.
Ejemplo: ¿Qué porcentaje es 40 de 120?
Cantidad
|
Porcentaje
|
120
|
100
|
40
|
x
|
Para resolverlo, se hace:
Resolvemos la incógnita (x):
Haciendo la operación, queda:
Simplificando y haciendo la división, queda:
Respuesta: 40 es el 33,33 % de 120.
Definición de tanto por ciento
El tanto por ciento de una cantidad es la parte correspondiente a dividir esa cantidad en 100 partes y después tomar la parte que se indica. También se le llama porcentaje.
Para que un porcentaje tenga sentido, debe ir relacionado a una cantidad de referencia. Por ejemplo:

Si tenemos 100 unidades de una determinada cantidad, es muy fácil obtener el tanto por ciento indicado, porque ya tenemos la cantidad dividida en 100 partes y sólo tenemos que coger las partes correspondiente.
Por ejemplo, el 20% de 100 es 20, ya que la parte resultante de dividir la cantidad en 1oo partes y después tomar 20.
Cuando se realiza el tanto por ciento, estamos tomando una parte del total. Así el 50% será la mitad de la cantidad, el 25% será la cuarta parte…
También es posible que el tanto por ciento sea mayor que 100, lo que significa que el porcentaje será mayor que la cantidad original.
TAREA PARA ENTREGAR EL JUEVES 8
1. La presa Temazcal, en el estado de Oaxaca, está al 63% de su capacidad, la cual es de 8.12 x 10^9 m^3. ¿Cuál es el volumen de agua que contiene la presa?2. Para ir del pueblito de Santiago al de San Marcos, existen dos caminos. El tiempo de recorrido para el primer trayecto es de 2 horas y 15 minutos; el del segundo es de 1 hora y 45 minutos.
a) ¿Qué porcentaje representa la duración del trayecto por el segundo camino respecto a la duración del segundo?
b) ¿Qué porcentaje representa la duración del trayecto por el segundo camino respecto a la duración del primero?
3. El costo de una casa hace 7 años erade $350,000, hoy es de $720,000.
a) ¿En qué porcentaje se incrementa su valor?
b) ¿Cuántas veces se incrementa el valor de un objeto, si decimos que su precio aumentó 100%?
c) ¿Cuántas veces se incrementa el valor de un objeto, si decimos que su precio aumentó 200%?
4. En el municipio de Santa Camila han sido vacunados contra la demencia 336 niños y ellos representan el 60% de la población infantil.
a) ¿Cuál es la población infantil en el municipio?
b? ¿Cuántos niños faltan por vacunar?
5. Esta quincena Lissette ahorró $3200, si esa cantidad representa 46% de su sueldo. ¿Cuál es su sueldo quincenal?
6. De los 800 alumnos de un colegio, han ido de viaje 600. ¿Qué porcentaje de alumnos ha ido de viaje?
7. Al adquirir un vehículo cuyo precio es de 8800 dólares, nos hacen un descuento del 7.5%. ¿Cuánto hay que pagar por el vehículo?
8. El precio de un ordenador es de 1200 dólares sin IVA. ¿Cuánto hay que pagar por él si el IVA es del 16%?
9. Se vende un objeto perdiendo el 20% sobre el precio de compra debido a la devaluación. Hallar el precio de venta del citado artículo cuyo valor de compra fue de 150 dólares.