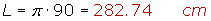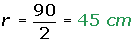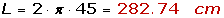MATE 1.Semana del 26 al 29 noviembre 2018
|
BLOQUE :
|
1
|
|
EJE:
|
Forma, espacio y medida
|
|
TEMA:
|
Magnitudes y medidas
|
|
SUBTEMAS:
|
Perímetro
del círculo
|
|
APRENDIZAJES ESPERADOS
|
Calcula el perímetro de polígonos y del círculo, áreas de triángulos
y cuadriláteros desarrollando y aplicando fórmulas
|
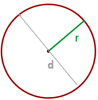
Radio de la circunferencia
El radio es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma.
Diámetro
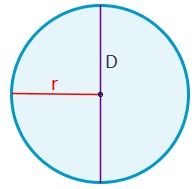El perímetro de un círculo es el doble del producto de π por el radio (r). También se puede calcular a partir del diámetro (D), siendo el producto de π y el diámetro.
Ejemplo 1
Sea un círculo de radio conocido, siendo éste r=2 cm.
Obtendremos el perímetro a partir del radio:
Y se obtiene que el perímetro de un círculo de radio 2 cm es de 12,57 cm.
¿Sabias que el famoso número pi (π), (la relación entre la longitud de una circunferencia y su diámetro), ya tenia una aproximación de cinco decimales en la Babilonia del siglo XX antes de J. C.
Los matemáticos griegos intentaban resolver la cuadratura del circulo (construir un cuadrado cuya área sea igual a la de un círculo dado).
En la misma época, Arquímedes, a base de dos polígonos regulares de 96 lados, uno inscrito y otro circunscrito, llega a un valor de π = 22/7, aproximación muy importante para su época.
Después, muchos matemáticos han buscado el valor de π, hasta que Lambert, en 1768, demuestra que π es un número irracional y en 1882, Lindemann demuestra la imposibilidad de la cuadratura del círculo.
Con la utilización de potentes ordenadores se ha llegado hasta 206 millones de decimales.
La función PI de Excel (hasta la versión actual Excel 2016) devuelve un valor de π con una aproximación de 15 decimales.
Una aproximación razonable para resolver ejercicios es π = 3,1416.
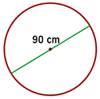
1 La rueda de un camión tiene 90 cm de radio. ¿Cuánto ha recorrido el camión cuando la rueda ha dado 100 vueltas?
Ejercicio 2
Supongamos que tenemos un círculo de diámetro conocido, siendo D=5 cm.
¿Cuál es su perímetro?
Ejercicio 3
Un ciclista participa en una competición con bicicleta con rueda lenticular trasera de 622 mm ø.
¿Cuántas vueltas habrá dado la rueda trasera de la bicicleta cuando el ciclista haya corrido 2 km?
|
| ||||
|
|
|
| ||
|
8.- Si una circunferencia mide 1.75 cm x π ¿Cuánto miden el radio y el diámetro?
9.- Escriban la relación que debe cumplirse entre el diámetro de un círculo (d), la longitud de la circunferencia (C) y el valor de π
-------- = π
