MATE 3. Semana del 28 Mayo al 1° Junio 2018
Forma, espacio y medida
Medida
• Análisis de las secciones que se obtienen al realizar cortes a un cilindro o a un cono recto. Cálculo de las medidas de los radios de los círculos que se obtienen al hacer cortes paralelos en un cono recto.
CÓNICAS
TAREA PARA ENTREGAR EL VIERNES 1° DE JUNIO
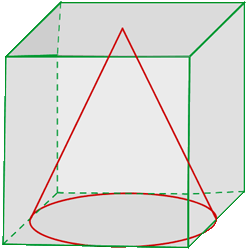
3. En un cubo de volumen un metro cúbico introducimos un cono cuya base está marcada por la circunferencia inscrita a la base del cubo. Si llenamos de agua el espacio que queda libre en el cubo, ¿qué volumen de agua necesiraríamos? Redondea a dos cifras decimales.
Medida
• Análisis de las secciones que se obtienen al realizar cortes a un cilindro o a un cono recto. Cálculo de las medidas de los radios de los círculos que se obtienen al hacer cortes paralelos en un cono recto.
CÓNICAS
Se entiende por CÓNICAS o SECCIONES CÓNICAS a las curvas planas que se producen por la intersección de un plano con un cono.
Las intersecciones del plano con el cono dependen del modo como éstas se produzcan. Cambiando el ángulo del plano y el lugar donde éste corta al cono, se producirán secciones diferentes.
Las intersecciones del plano con el cono dependen del modo como éstas se produzcan. Cambiando el ángulo del plano y el lugar donde éste corta al cono, se producirán secciones diferentes.
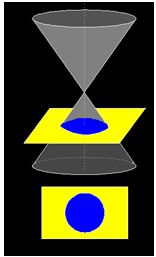
En el siguiente dibujo tienes una cartulina amarilla que “corta”
perpendicularmente al eje del cono y compruebas que la sección es el círculo en azul, siempre que el corte no se produzca por el vértice. Su contorno es una circunferencia.
Estudiaremos su contorno, es decir, la circunferencia.
Estudiaremos su contorno, es decir, la circunferencia.
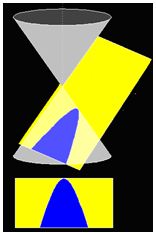
Si el plano corta oblicuamente al eje del cono y a todas sus generatrices, sin pasar por el vértice, la sección que obtenemos es una elipse.
Mantenemos la misma cartulina amarilla y la sección resultante en azul:
Si el corte lo hacemos, de forma oblicua al eje del cono pero paralela a la generatriz del mismo obtenemos una parábola:
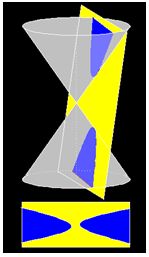
Si el plano corta a las generatrices en ambos lados del vértice del cono, obtenemos una hipérbola.
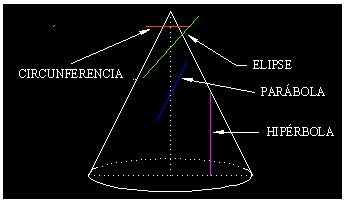
Si te fijas en la figura siguiente, a las cónicas podemos clasificarlas teniendo en cuenta el ángulo que forman el plano con el eje del cono:
El área de un polígono regular se calcula a partir de su perímetro y su apotema. Sea P el polígono regular con N lados, su área es:
En un polígono regular, el perímetro se puede determinar por el producto del número de lados por la longitud de uno de los lados, es decir, Perímetro=N·L. O sea:
TAREA PARA ENTREGAR EL VIERNES 1° DE JUNIO
Resuelve los siguientes problemas:
1Calcula el volumen de papel higiénico que hay en el siguiente rollo. Redondea a dos cifras decimales.
2. Calcular la altura de un cono de helado cuyo diámetro mide 5 cm y su volumen es de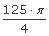 
m3. Redondea a dos cifras decimales.
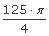m3. Redondea a dos cifras decimales.
h = cm
Si en vez de colocar una sola bola de helado en el cono, lo llenásemos entero, ¿qué volumen de helado necesitaríamos?
V = cm3
Para no mancharnos el cono se envuelve con un papel con la misma forma pero con 3 cm menos de altura. ¿Qué cantidad de papel es la que usamos?
A = cm2
3. En un cubo de volumen un metro cúbico introducimos un cono cuya base está marcada por la circunferencia inscrita a la base del cubo. Si llenamos de agua el espacio que queda libre en el cubo, ¿qué volumen de agua necesiraríamos? Redondea a dos cifras decimales.
