MATE 1. Semana del 7 al 11 Mayo 2018

Manejo de la información

Proporcionalidad y funciones 

• Análisis de la regla de tres, empleando valores enteros o fraccionarios.

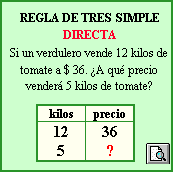
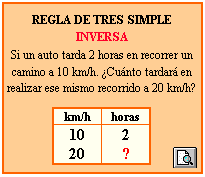
REGLA de TRES SIMPLE

Se llama razón al cociente entre dos números y se llama proporción a la igualdad de  dos razones.

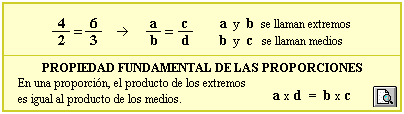Los problemas en los que los elementos mantienen una relación proporcional directa o  inversa se resuelven mediante la regla de tres simple.

La regla de tres o regla de tres simple es una forma de resolver problemas de proporcionalidad entre tres valores conocidos y una incógnita, estableciendo una relación de proporcionalidad entre todos ellos.

Es decir, lo que se pretende con ella es hallar el cuarto término de una proporción conociendo los otros tres.

En la regla de tres simple se establece, por tanto, la relación de proporcionalidad entre dos valores conocidos A y B , y conociendo un tercer valor C, se calcula un cuarto valor D.

Dicha relación de proporcionalidad existente entre A y B puede ser directa o inversa.

Será directa cuando, dentro de esa proporcionalidad, a un mayor valor de A le corresponda también un mayor valor de B (o a un menor valor de A le corresponda un menor valor de B), y será inversa, cuando a un mayor valor de Ale corresponda un menor valor de B (o a un menor valor de A le corresponda un mayor valor de B).

En el primer caso tenemos una regla de tres simple directa, y en el segundo caso una regla de tres simple inversa.

Vamos a ver cada una más detalladamente.

Regla de tres simple directa

Tenemos que:

En la regla de tres simple directa, en la relación entre los valores, se cumple que:

y decimos que A es a B directamente proporcional, como C es a D.

De esta igualdad anterior, se deduce fácilmente que, por ejemplo, si conocemos los valores A, B y C, y queremos calcular D, éste último será:

Lo vemos con un ejemplo.

“Una sandía cuesta en el supermercado 4 euros. Juán ha comprado 50 sandías ¿cuánto se habrá gastado?”

Pero… ¿quién compra 50 sandías? ¿las metes todas en el maletero del coche? A no ser que Juán tenga un puesto de frutas en el mercado… ¡se le van a estropear antes de que se las pueda comer todas!

Aprovechando que este fin de semana he estado pintando una habitación, vamos a verlo con un ejemplo algo más real:

“María tiene que comprar pintura blanca para darle una mano previa a una habitación que quiere cambiar de color. Si en el bote de pintura se indica que con 1 litro de pintura se pueden pintar 8 m2 ¿cuántos litros necesita teóricamente para pintar las paredes de la habitación si ésta tiene 40 m2 de pared?”

En este caso, la relación de proporcionalidad es directa, puesto que cuanto másmetros cuadrados de pared tengamos que pintar más litros de pintura necesitaremos. Lo hacemos como hemos visto antes:

María necesitará, por tanto, 5 litros de pintura.

Regla de tres simple inversa

En este caso tenemos que:

En la regla de tres simple inversa, en la relación entre los valores, se cumple que:

y decimos que A es a B inversamente proporcional, como C es a D.

Conocidos los valores A, B y C, el valor D será:

Por ejemplo: “Un grifo con un caudal de salida de agua de 18 litros por minuto tarda 14 horas en llenar un depósito. ¿Cuánto tardaría si su caudal fuera de 7 litros por minuto?”

La relación de proporcionalidad es inversa, ya que cuanto más caudal de salida de agua tiene el grifo menos tiempo (en horas) se necesita para llenar el depósito. Tenemos así que:

Con un grifo de 7 litros por minuto de caudal (menos caudal) necesitamos 36 horas (más tiempo) para llenar el depósito.

Bien, hasta ahora hemos visto cómo resolver problemas de proporcionalidad entre tres valores conocidos y una incógnita, estableciendo una relación de proporcionalidad entre todos ellos y utilizando la regla de tres simple que corresponda, directa o inversa.

TAREA PARA ENTREGAR EL VIERNES 11 DE MAYO

1. Problemas de reducción a la unidad. EJEMPLO:

    He aquí un problema: 3 cajas de bombones valen 6 euros. ¿Cuántos euros vale una caja?
    Una caja valdrá 6 euros : 3 cajas = 2 euros cada caja.
    Este tipo de problemas se llaman de "reducción a la unidad" porque se busca de lo que toca de una cosa para una unidad de la otra.
    De problema anterior se podría preguntar otra cosa: ¿Cuántas cajas puedo comprar con un euro?
    En este caso habrá que dividir las cajas entre los euros. 3 cajas : 6 euros = 0,5 cajas puedo comprar con un euro.

    Puedes leer el tema de cómo resolver problemas.
    Haz estos problemas EN TU CUADERNO y contesta con la solución correcta.

1. Si 8 kilos de manzanas valen 16 euros, ¿cuántos euros vale un kilo?
2. De problema anterior, ¿cuántos kilos podré comprar con un euro?
3. Tengo 12 botellas de vino y me han costado 120 euros. ¿Cuántos euros vale una botella?
4. Del problema anterior, ¿cuántas botellas puedo comprar con un 1 euro?
5. Si 500 ruedas de metal pesan 3000 kilos, ¿cuántos kilos pesa cada rueda?
6. Del problema anterior, ¿cuántas ruedas podré hacer con 1 kilo?

 2.- Regla de tres directa.

    Después de saber cuánto vale una unidad podemos saber cuánto valen otras unidades.
    Una forma resumida es aplicar la regla de tres.
    Veamos un ejemplo: 3 paquetes de cigarros valen 6 euros, ¿cuánto valdrán 10 paquetes?
    Nos dan tres datos y nos falta uno que es la incógnita.

                    Si 3 paquetes (A) cuestan   6 euros (B)
                        10 paquetes (C) costarán    x      (D)

    Un paquete valdrá 2 euros (6:3)  y 10 paquetes 20 euros (2 x 10). También multiplicamos  (6 x 10) y dividimos por 3. Salen 20 euros.
    Haciendo el problema por la regla de tres, multiplicamos los números medios B y C y dividimos por el extremo A; (6 x 10) : 3 = 20 euros.
    Hay que cuidar que las cantidades A y C sean de la misma especie. En este caso paquetes.

    Otro ejemplo: Hemos hecho el recorrido de 560 kilómetros con el coche en 8 horas. Cúantos kilómetroa recorreremos en 12 horas.

                    Si en 8 horas (A)   ------>   560 km (B)
                        en 12 horas (C)  ------>     x      (D)

    x = (560 x 12) : 8 = 6720 : 8 = 840 kilómetros.

    En general, la regla de tres con magnitudes directamente proporcionales se resuelve multiplicando los términos medios ( B y C ) y dividiendo por el extremo A.

    Resuelve estos problemas:

1. Unos 6 kilos de bombones cuestan 6,3 euros, ¿cuánto costarán 12 kilos?
2. Un obrero fabrica 200 piezas en 5 horas. ¿Cuántas piezas puede fabricar en 48 horas?
3. Un pintor tarde 3 horas en pintar 30 cuadros.¿Cuánto tardará en pintar 200 cuadros?
4. Un montador cobra 72 euros por 40 horas de trabajo.¿Cuánto cobrará por 80 horas?
5. Con 12 kilogramos de manzanas se obtienen 7 litros de sidra. ¿Cuántos litros se obtendrán con 48 kg?
6. Si 8 metros de cable cuestan 13 euros, ¿cuánto costarán 16 metros?

 3.- Regla de tres inversa. 

    En las cantidades inversamente proporcionales al aumentar una, disminuye la otra.
    Ejemplo: La velocidad de un automóvil y el tiempo que tarda en recorrer una distancia. A más velocidad, menos tiempo tardará.

    Veamos este ejemplo: 12 albañiles construyen una casa en 60 días. ¿Cuánto tardarán 2 albañiles en construirla? (con menos albañiles tardarán más tiempo, luego es inversa).

                    Si 12 albañiles (A) tardan        60 días (B)
                        2 albañiles (B) tardarán           x   (D)

    Un sólo albañil tardará (12 x 60) = 720 días. Dos albañiles, la mitad  720 : 2 = 360 días.
    Con la regla de tres multiplicamos las dos primeras cantidades A y B y dividimos por la C.
    D = (A x B) : C

    En general, la regla de tres con magnitudes inversamente proporcionales se resuelve multiplicando los dos primeros términos (A y B) y dividiendo por el tercero (C).

    Resuelve estos problemas:

1. Unos 30 soldados cavan una trinchera en 5 días. ¿Cuántos días le costarán a 15 soldados?
2. Un coche de Teruel a Zaragoza tarda 3 horas a una velocidad de 80 kilómetros por hora. ¿Cuántas horas tardará a una velocidad de 120 km por hora?
3. Unos 5 albañiles tardan 45 días en hacer un chalet. ¿Cuántos días tardarán en hacerlo 15 albañiles?
4. Leyendo 20 páginas cada día terminé un libro en 33 días. ¿Cuántos días tardaré leyendo 30 páginas diarias?