MATE 2. Semana del 7 al 11 de Mayo 2018

Manejo de la información

Proporcionalidad y funciones

• Análisis de las características de una gráfica que represente una relación de proporcionalidad en el plano cartesiano.

Características de una grafica que representa una relación de proporcionalidad en el plano cartesiano 
¿ que es un plano cartesiano ?

¡El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto.

¡El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados. Las coordenadas se forman asociando un valor del eje de las "X" y uno de las "Y", respectivamente, esto indica que un punto se puede ubicar en el plano cartesiano con base en sus coordenadas

Ubicación de los puntos de el plano cartesiano

Plan de clase (1/4)

Curso: Matemáticas 8                      Eje temático: MI

Contenido: 8.4.4 Análisis de las características de una gráfica que represente una relación de proporcionalidad en el plano cartesiano.

Intenciones didácticas: Que los alumnos reflexionen sobre la manera de ubicar puntos en el plano cartesiano.

Consigna: En equipos, resuelvan la siguiente actividad.

A partir de la siguiente figura dibujada en el primer cuadrante del plano cartesiano, construyan la figura simétrica A’B’C’D’ con respecto al eje vertical. Posteriormente contesten lo que se pide.

			a) ¿Cuáles son las coordenadas de los puntos A, B, C y D? b) ¿Cómo se llama a la primera componente de cada par ordenado? c) ¿Cómo se llama a la segunda componente de cada par ordenado? d) ¿Cuáles son las coordenadas de los puntos A’, B’, C’ y D’?
Consideraciones previas:

Los alumnos ya han manejado el plano cartesiano en otros cursos, es conveniente que se use la terminología correspondiente; par  ordenado, abscisa, ordenada, eje de las abscisas, eje de las ordenadas, origen del plano cartesiano, cuadrantes.

Si la actividad resulta fácil y el tiempo lo permite, conviene agregar las siguientes:

a)    Si a la primera coordenada de cada vértice del cuadrado ABCD le sumamos dos unidades. ¿Qué transformación sufriría la figura? ¿Cuáles serían las nuevas coordenadas de los vértices?

b)    Si a la segunda coordenada de cada vértice del cuadrado ABCD le restamos cinco unidades. ¿Qué transformación sufriría la figura? ¿Cuáles serían las nuevas coordenadas de los vértices?

Las expresiones de proporcionalidad directa tienen la forma y = kx

k es un valor constante que se le llama pendiente y se le pone también la letra m

Representación de la variación y=ax+b

Representación de la variación  y=ax+b

a, b son valores que nunca cambian.

Las expresiones que tienen una constante que se les va sumando nunca pasan por el origen

Función lineal

La función lineal es del tipo: y = mx

Su gráfica es una línea recta que pasa por el origen de coordenadas.

Ejemplo

y = 2x

x	0	1	2	3	4
y = 2x	0	2	4	6	8

Pendiente

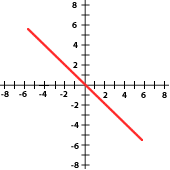
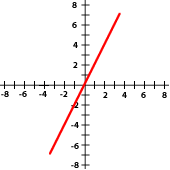
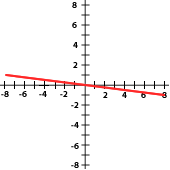
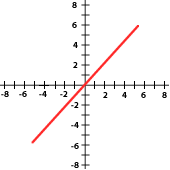
La pendiente es la inclinación de la recta con respecto al eje de abscisas.

Si m > 0 la función es creciente y ángulo que forma la recta con la parte positiva del eje OX es agudo.

Si m < 0 la función es decreciente y ángulo que forma la recta con la parte positiva del eje OX es obtuso.

TAREA PARA ENTREGAR EL VIERNES 11 DE MAYO

1. El par ordenado $(a, b)$left parenthesis, a, comma, b, right parenthesis da la ubicación del punto $P$P en el plano coordenado. El valor de $a$a es $0$0, pero $b$b no es cero.

¿Dónde puede estar ubicado el punto $P$P en el plano coordenado?

Elige todas las respuestas adecuadas:

Elige todas las respuestas adecuadas:

Elige todas las respuestas adecuadas:

• 
  

  
  

  Cuadrante I
• 
  

  
  

  Cuadrante II
• 
  

  
  

  Cuadrante III
• 
  

  
  

  Cuadrante IV
• 
  

  
  

  Eje $x$x
• 
  

  
  

  Eje $y$

2.   Coloca el punto  $(-2.5,2)\; en\; un\; plano\; cartesiano\; que\; tú\; dibujes,$luego selecciona su ubicación en el plano coordenado.

$y$$x$

Dónde se ubica $(-2.5,2)$left parenthesis, minus, 2, point, 5, comma, 2, right parenthesis en el plano coordenado?

Escoge 1 respuesta:

• 
  

  
  

  Primer cuadrante
• 
  

  
  

  Segundo cuadrante
• 
  

  
  

  Tercer cuadrante
• 
  

  
  

  Cuarto cuadrante
• 
  

  
  

  Eje $x$x
• 
  

  
  

  Eje $y$

3. Selecciona el cuadrante o el eje en el plano coordenado donde se ubica cada par ordenado.

	C I	C II	C III	C IV	Eje $x$x	Eje $y$y
$(8,3)$left parenthesis, 8, comma, 3, right parenthesis
$(9,-2)$left parenthesis, 9, comma, minus, 2, right parenthesis
$(-3.5,-6)$left parenthesis, minus, 3, point, 5, comma, minus, 6, right parenthesis

4.

La coordenada $x$x del punto $E\text{}$E es negativa y su coordenada $y$y no es $0$0.

¿Dónde puede estar ubicado el punto $E$E en el plano coordenado?

Elige todas las respuestas adecuadas:

Elige todas las respuestas adecuadas:

• 
  

  
  

  Cuadrante I
• 
  

  
  

  Cuadrante II
• 
  

  
  

  Cuadrante III
• 
  

  
  

  Cuadrante IV
• 
  

  
  

  Eje $x$x
• 
  

  
  

  Eje $y$y

Completa las siguientes tablas de funciones lineales según indique cada uno de los enunciados:

1María va a la frutería y compra plátanos a 1.70 €/Kg.

Cantidad (en Kg)	0	1	2			7
Precio (en €)	0			5.1	8.5

2Un número y su doble.

Número	−3	−2	−1	0	1	2	3
Doble

Para dibujar la gráfica de una función lineal basta hacer una tabla de valores con dos valores, pero podemos tomar tres para orientarnos mejor. Completa las siguientes tablas de valores correspondientes a las funciones lineales señaladas en cada caso.

3Completa la tabla de valores de la función lineal y = 3x

x	y
−3	−9
0
2

4Completa la tabla de valores de la función lineal y = −5x

x	y
−2
	−5
3

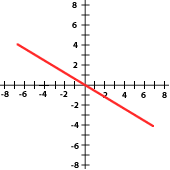
5 Relaciona cada gráfica a su expresión correspondiente:

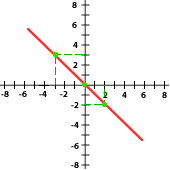
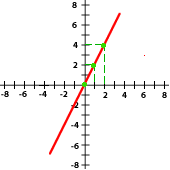
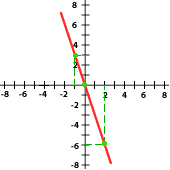
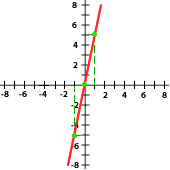
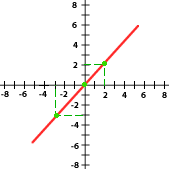
y = 2x

y = −3x

y = x

y = −x

y = 5x

a)  y = x   b) y = -3x    c) y = 2x    d) 5x   e) y =-x

6Indica si las gráficas  siguientes sus pendientes son positivas o negativas: