MATE 3. Semana del 24 de febrero al 6 marzo 2020
Bloque:
|
2
|
Eje:
|
Forma, espacio y medida.
|
TEMA:
|
Magnitudes y medidas
|
Contenido:
|
23. La pendiente, la tangente y el ángulo de inclinación de una recta
|
APRENDIZAJES ESPERADOS:
|
• Análisis de las relaciones entre el valor de la pendiente de una
recta, el valor del ángulo que se forma con la abscisa y el cociente del
cateto opuesto sobre el cateto adyacente.
|
El video de abajo puede ser omitido si ves los otros dos. Para un mejor entendimiento y que éste sea más pausado, te aconsejo que lo veas
ppppppppp
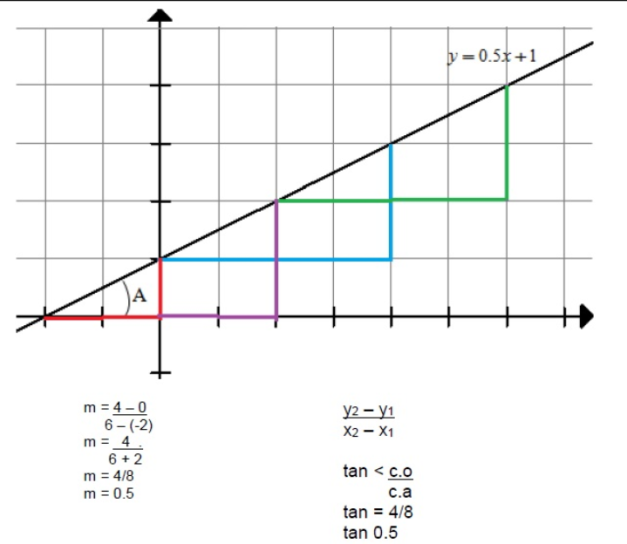
Realiza cualquiera de los apuntes 1 y 2. El tercer apunte es obligatorio
Apunte 1
Se denota con la letra m.
Si m > 0 la función es creciente y ángulo que forma la recta con la parte positiva del eje OX es agudo.

Si m < 0 la función es decreciente y ángulo que forma la recta con la parte positiva del eje OX es obtuso.

La pendiente de una recta es la tangente del ángulo que forma la recta con la dirección positiva del eje de abscisas.
Cálculo de la pendiente
Ejemplos
La pendiente de la recta que pasa por los puntos A(2, 1), B(4, 7) es:

La recta que pasa por los puntos A(1, 2), B(1, 7) no tiene pendiente, ya que la división por 0 no está definida.

Seno, coseno y tangente
Tres funciones, la misma idea.
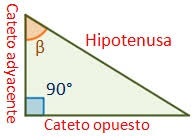
Triángulo rectángulo
Antes de concentrarnos en las funciones, nos ayudará dar nombres a los lados de un triángulo rectángulo, de esta manera:
(Adyacente significa tocando el ángulo, y opuesto es opuesto al ángulo... ¡claro!)
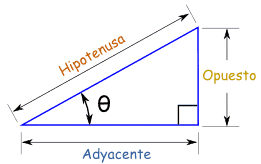
Seno, coseno y tangente
Las tres funciones más importantes en trigonometría son el seno, el coseno y la tangente. Cada una es la longitud de un lado dividida entre la longitud de otro... ¡sólo tienes que aprenderte qué lados son!
Para el ángulo θ :
Para el ángulo θ :
Función seno:
| sin(θ) = Opuesto / Hipotenusa |
Función coseno:
| cos(θ) = Adyacente / Hipotenusa |
Función tangente:
| tan(θ) = Opuesto / Adyacente |
Nota: el seno se suele denotar sin() (por la palabra inglesa "sine") o sen(). Aquí utilizaremos sin() pero puedes encontrarte la otra notación en otros libros o sitios web.
Sohcahtoa
Sohca...¿qué? ¡Sólo es una manera de recordar qué lados se dividen! Así:
Soh...
|
Seno = Opuesto / Hipotenusa
|
...cah...
|
Coseno = Adyacente / Hipotenusa
|
...toa
|
Tangente = Opuesto / Adyacente
|
Apréndete "sohcahtoa" - ¡te puede ayudar en un examen!
Ejemplos
Ejemplo 1: ¿cuáles son el seno, coseno y tangente de 30° ?
El triángulo clásico de 30° tiene hipotenusa de longitud 2, lado opuesto de longitud 1 y lado adyacente de longitud √3: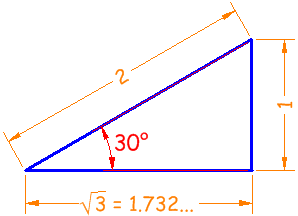
Seno
|
sin(30°) = 1 / 2 = 0.5
|
Coseno
|
cos(30°) = 1.732 / 2 = 0.866
|
Tangente
|
tan(30°) = 1 / 1.732 = 0.577
|
(¡saca la calculadora y compruébalo!)
Ejemplo 2: ¿cuáles son el seno, coseno y tangente de 45°?
El triángulo clásico de 45° tiene dos lados de 1 e hipotenusa √2: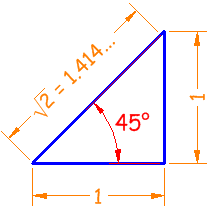
Seno
|
sin(45°) = 1 / 1.414 = 0.707
|
Coseno
|
cos(45°) = 1 / 1.414 = 0.707
|
Tangente
|
tan(45°) = 1 / 1 = 1
|
Ejercicio
Prueba este ejercicio sobre el papel donde tienes que calcular la función seno para ángulos de 0° a 360°, y dibujar el resultado. Te ayudará a entender estas funciones que son bastante simples.
Funciones menos comunes
Para completar el cuadro, hay otras 3 funciones donde divides un lado por otro, pero no se usan tanto.
Son iguales a 1 divivido entre las tres funciones básicas (sin, cos y tan), así:
Función secante:
| sec(θ) = Hipotenusa / Adyacente | (=1/cos) |
Función cosecante:
| csc(θ) = Hipotenusa / Opuesto | (=1/sin) |
Función cotangente:
| cot(θ) = Adyacente / Opuesto | (=1/tan) |
Apunte 3
Graficando Ecuaciones con Forma Pendiente-Intersección
Objetivos de Aprendizaje
· Escribir una ecuación lineal en su forma pendiente-intersección y definir sus partes.
· Graficar una recta usando la fórmula pendiente-intersección y derivar la ecuación de la recta a partir de la gráfica.
Introducción
Las líneas rectas son producidas por funciones lineales. Esto significa que una línea recta puede ser descrita por una ecuación que tenga la forma de de una ecuación lineal, 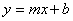 . En ésta fórmula, y es la variable dependiente, x es la variable independiente, m es una constante de tasa de cambio, y b es el ajuste que mueve la función con respecto al origen. En una ecuación más general de la línea recta, x y y son coordenadas, m es la pendiente, y b es la [intersección en y]. Como la ecuación describe una recta en términos de su pendiente y su intersección en y, ésta ecuación se llama forma pendiente-intersección.
. En ésta fórmula, y es la variable dependiente, x es la variable independiente, m es una constante de tasa de cambio, y b es el ajuste que mueve la función con respecto al origen. En una ecuación más general de la línea recta, x y y son coordenadas, m es la pendiente, y b es la [intersección en y]. Como la ecuación describe una recta en términos de su pendiente y su intersección en y, ésta ecuación se llama forma pendiente-intersección.
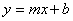 . En ésta fórmula, y es la variable dependiente, x es la variable independiente, m es una constante de tasa de cambio, y b es el ajuste que mueve la función con respecto al origen. En una ecuación más general de la línea recta, x y y son coordenadas, m es la pendiente, y b es la [intersección en y]. Como la ecuación describe una recta en términos de su pendiente y su intersección en y, ésta ecuación se llama forma pendiente-intersección.
. En ésta fórmula, y es la variable dependiente, x es la variable independiente, m es una constante de tasa de cambio, y b es el ajuste que mueve la función con respecto al origen. En una ecuación más general de la línea recta, x y y son coordenadas, m es la pendiente, y b es la [intersección en y]. Como la ecuación describe una recta en términos de su pendiente y su intersección en y, ésta ecuación se llama forma pendiente-intersección.
DebES notar que cambiando el valor de m puedes girar la recta de horizontal hasta casi vertical, pasando por cada pendiente. Cuando m, la pendiente, aumenta, la recta se hace más pronunciada. Cuando m disminuye, la pendiente se aplana.
Cambiando el valor de b la recta se mueve a lo largo del eje y. Un valor positivo de la intersección en y significa que la recta cruza el eje y sobre el origen, mientras que un valor negativo de la intersección en y significa que la recta cruza por debajo del origen.
Cambiando los valores de m y b, podemos fácilmente definir una recta. Es por eso que la fórmula pendiente-intersección es tan útil.
EJEMPLO
Ahora que entendemos la forma pendiente-intersección, podemos ver la gráfica de una recta y escribir su ecuación tan sólo identificando la pendiente y la intersección en y. Intentémoslo con ésta recta:

La forma pendiente-intersección es 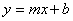 . Para ésta recta, la pendiente es
. Para ésta recta, la pendiente es 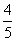 , y la intersección en y es 4. Si sustituimos esos valores en la fórmula, generamos la ecuación
, y la intersección en y es 4. Si sustituimos esos valores en la fórmula, generamos la ecuación 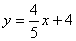 . La cual es la ecuación pendiente-intersección de nuestra recta.
. La cual es la ecuación pendiente-intersección de nuestra recta.
De Ecuación a Gráfica
Hemos visto que no es difícil convertir la gráfica de una recta a una ecuación. También podemos trabajar en la otra dirección y producir una gráfica a partir de la ecuación pendiente-intersección. Considera la ecuación 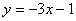 . Ésta ecuación nos dice que la intersección en y ocurre en -1. Empezamos por graficar ese punto, (0, -1), en la gráfica.
. Ésta ecuación nos dice que la intersección en y ocurre en -1. Empezamos por graficar ese punto, (0, -1), en la gráfica.

La ecuación también nos da la pendiente de la recta, que es -3. Por lo que contamos 3 unidades por encima de -1 y graficamos el segundo punto. Luego dibujamos una línea a través de estos dos puntos, y ahí la tenemos, la gráfica de 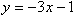 .
.
Sumario
La forma pendiente-intersección de una ecuación lineal se escribe como 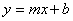 , donde m es la pendiente y b es el valor de y en la intersección en y. Como sólo necesitamos saber la pendiente y la intersección en y para escribir ésta fórmula, es muy fácil derivar la ecuación de la recta a partir de la gráfica o trazar la gráfica a partir de la ecuación.
, donde m es la pendiente y b es el valor de y en la intersección en y. Como sólo necesitamos saber la pendiente y la intersección en y para escribir ésta fórmula, es muy fácil derivar la ecuación de la recta a partir de la gráfica o trazar la gráfica a partir de la ecuación.

- A: y=6x+4
- B: y=60x+4
- C: y=6x+40
- D: y=60x+40
2. Durante un sexenio el incremento del costo del pasaje del transporte público aumentó lo mismo cada año. En el primer año del sexenio el costo era de $ 3.5 y para el ultimo año era de $ 11, el comportamiento está en la gráfica siguiente:

- A: $ 0.5
- B: $ 1.0
- C: $ 1.5
- D: $ 2.0
3. Observa el siguiente dibujo que representa una resbaladilla:

- A: 25 m
- B: 14 m
- C: 5 m
- D: 4 m
- 4.
- Juan quiere fijar una antena de 52 m de altura con un cable que vaya de la mitad de la misma al suelo. El cable hace un ángulo de 40° respecto al suelo, como se muestra en la figura:

- A: 80.8976 m
- B: 67.8811 m
- C: 40.4488 m
- D: 33.9405 m
- 5.
Un tejado con inclinación de 55° respecto a la vertical se soporta en un marco de madera en forma de triángulo- rectángulo. Si la pieza vertical del marco mide 1.40m entonces, ¿Cuál de las siguientes expresiones nos representa el valor de la medida x que es la longitud horizontal del marco de madera?
A) (1.40) (tan 55°)
B) (1.40)(sen 55°)
C) (tan 55°)/1.40
D) (cos 55°)/1.40
B) (1.40)(sen 55°)
C) (tan 55°)/1.40
D) (cos 55°)/1.40

6.
- Observa el siguiente triángulo-rectángulo, ¿Cuál de los siguientes cocientes identifica a la razón tangente del ángulo B?
A) 4/3
B) 4/5
C) 3/4
D) 3/4
B) 4/5
C) 3/4
D) 3/4

7.
- A Nacho que es el jefe de constructores el arquitecto le dijo que para trazar el puente vehicular debo considerar que la subida tiene una inclinación de 30° y una altura máxima de 23 m, tal como se muestra en el dibujo, con base en estos datos Nacho tiene que calcular la longitud total de la vía en posición diagonal que descansa sobre el soporte de 23 m, ¿cuál debe ser su tamaño? (sen30°= 0.5, cos30°=0.86, tan30°=0.57)
A) 26.5 m
B) 46.0 m
C) 19.9 m
D) 11.5 m
B) 46.0 m
C) 19.9 m
D) 11.5 m

8. Camilita encontró en su libro la figura de abajo (estaba estudiando para su examen de mate y no fue a ver al novio):
Quiere conocer el coseno del ángulo B, y tiene como dato que seno de ese mismo ángulo es 0.9396 y la tangente es 2.7474, ¿cuál será el valor correcto del coseno?
A) 0.3420
B) 0.9396
C)2.7474
D)2.92389. Calcula la altura de la torre si nuestro personaje está a 7 m de la base de la torre, el ángulo con el que está observando la cúspide es de 60º y sostiene el artilugio a una altura de 1,5 m.

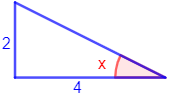
10. Calcular el valor de x
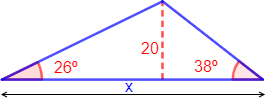
11. Calcular la base (lado x) del siguiente triángulo escaleno
12. Desde un supermercado se observa el ático de un rascacielos de 527 metros de altura bajo un ángulo de 42°. Calcular la distancia que hay desde el supermercado hasta la puerta del rascacielos.
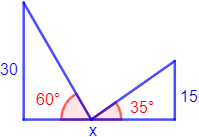
13. Calcular la base (lado x) de la siguiente figura construida con dos triángulos rectángulos:
14. ¿Cuál es la ecuación de la recta en la siguiente gráfica?
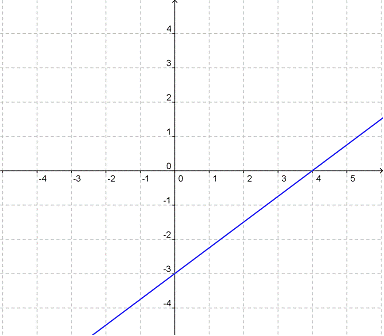
A) 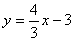
B) 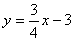
C) 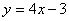
D) 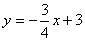
15. ¿Qué gráfica muestra la recta
A) 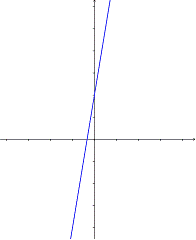 B)
B) 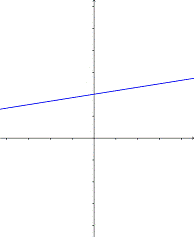
 B)
B) 
C) 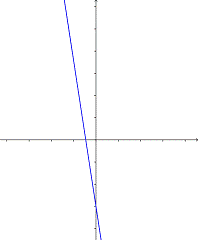 D)
D) 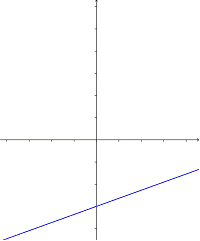
 D)
D) 
16. Escribe la ecuación de la recta que tiene pendiente
17. ¿Cuál es la ecuación de una recta que tiene pendiente −2 y pasa por el punto (0, 8)?
A) y = −2x + 8
B) y = 8x – 2
C) y = −2x + 0
D) 0 = 8x – 2
18. Encuentre la ecuación de la recta mostrada.

19. Hallar la ecuación de la recta que tiene pendiente m = 3 y b = 10 .
20. La ecuación en forma explícita de la recta que pasa por A (1,5) y tiene como pendiente m=-2 es:
21.Escribe la ecuación de la recta que interseca al eje
y en left parenthesis, 0, comma, minus, 7, right parenthesis y cuya pendiente es 5.
y, equals
23. Encuentra la ecuación de la recta.
24. Encuentra la ecuación de la recta.
25. Encuentra la ecuación de la recta.





