MATE 1. Semana del 10 al 14 de febrero 2020

BLOQUE:	2
EJE:	Número, álgebra y variación
TEMA:	Funciones
SUBTEMA:	18. Variación lineal a partir de datos en tablas y gráficas.
APRENDIZAJES ESPERADOS:	Analiza y compara situaciones de variación lineal a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con estos tipos de variación.

Identifica los elementos de un plano cartesiano. Son las bases para el ejercicio de este desafío.
El plano cartesiano se forma con cuatro cuadrantes definidos por dos ejes, uno horizontal, nombrado con la letra x; y uno vertical nombrado con la letra y.
Tiene un punto de origen localizado en el punto donde se cruzan los dos ejes y se identifica con el número cero.En el eje horizontal, del 0 a la derecha se identifican los números positivos; y del 0 a la izquierda, los negativos.En el eje vertical, del 0 hacia arriba, se identifican los números positivos; y del 0 hacia abajo, los negativos.

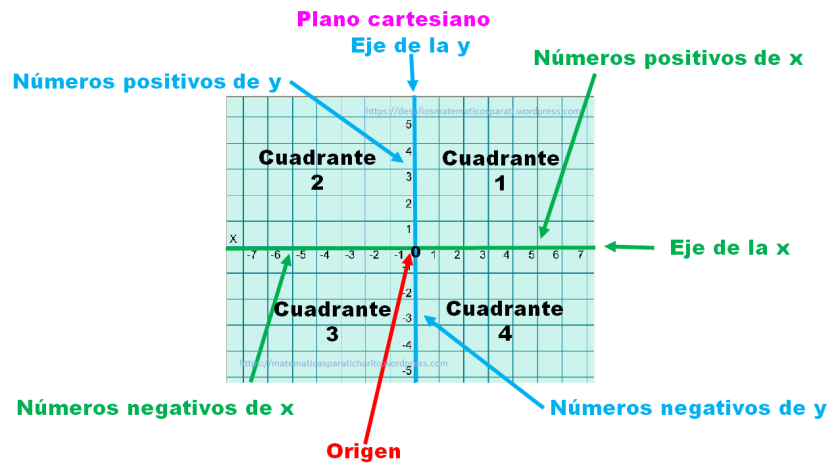
Una coordenada se forma con una pareja de números separados por una coma y escritos dentro de un paréntesis. El primer número es conocido como abscisa y el segundo como ordenada.

La coordenada sirve para ubicar un punto en el plano cartesiano
El número de la abscisa se ubica contando en el eje x, mientras que el de la ordenada se cuenta en el eje de y.

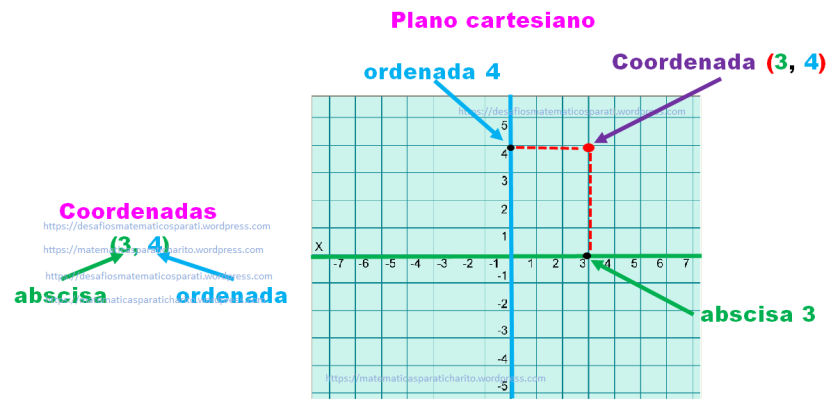
Para este ejercicio sólo trabajarás con el primer cuadrante formado por los números positivos de los dos ejes.


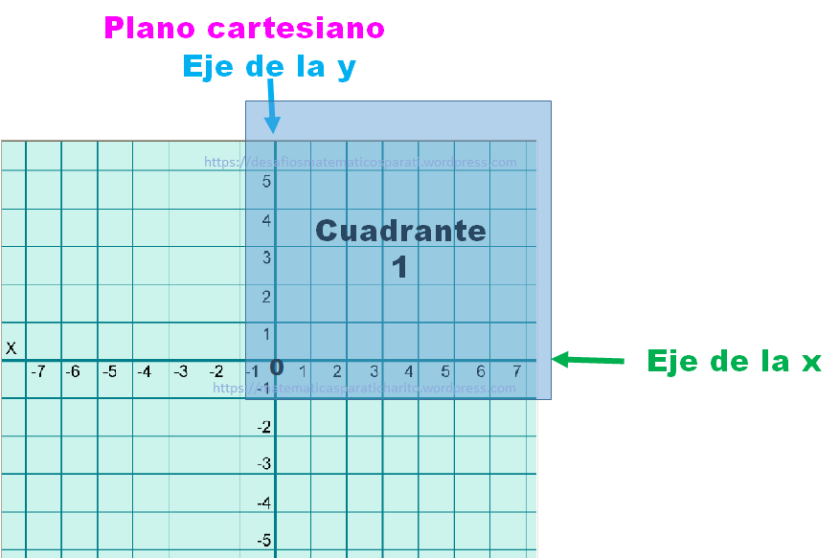
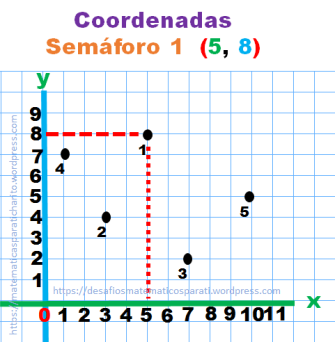
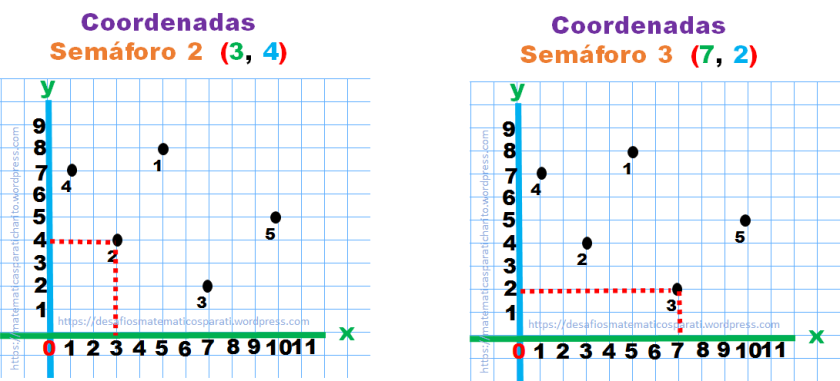
Ubica las coordenadas donde se encuentran los cinco semáforos. Recuerda escribir dentro del paréntesis, primero el número de la abscisa y después el de la ordenada separados con una coma.
Yo los ubicaré en una cuadrícula y los marcaré con puntos.

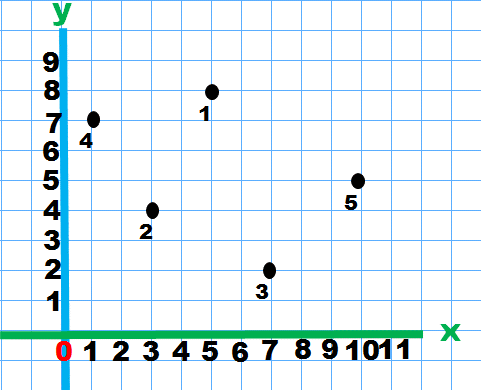
Encontremos los puntos donde se cruzan la abscisa y la ordenada, son los puntos donde se están los semáforos.



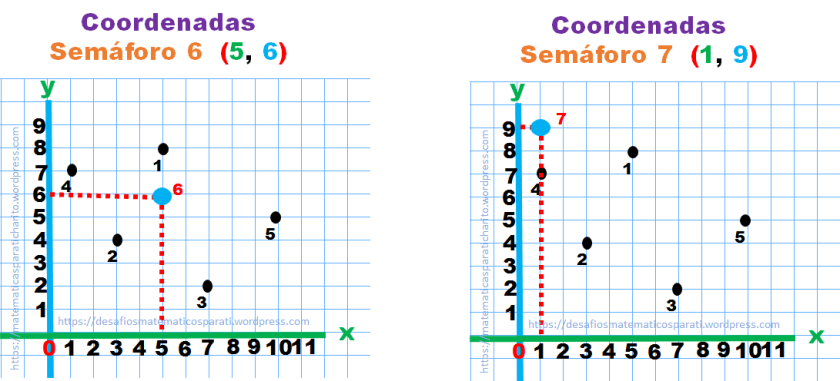
Para ubicar el semáforo seis con las coordenadas (5,6), ubica primero el 5 en la numeración horizontal y después el 6, en la vertical. Haz lo mismo para ubicar el semáforo siete con la coordenada (1,9)

En matemáticas, las tres formas principales de representar una relación son una tabla, una gráfica o una ecuación. En este artículo, representaremos la misma relación de las tres maneras para ver cómo funciona cada una.

Ejemplo de una relación: Una compañía de pizzas vende la pizza pequeña en $\$6$dollar sign, 6. Cada ingrediente cuesta $\$2$dollar sign, 2.

Representación por medio de una tabla

Sabemos que el costo de una pizza con $0$0 ingredientes es de $\$6$dollar sign, 6; una pizza con $1$1 ingrediente cuesta $\$2$dollar sign, 2 más, es decir, $\$8$dollar sign, 8, y así sucesivamente. A continuación mostramos una tabla que exhibe este hecho:

Ingredientes en la pizza $(x)$left parenthesis, x, right parenthesis	Costo total $(y)$left parenthesis, y, right parenthesis
$0$0	$\$6$dollar sign, 6
$1$1	$\$8$dollar sign, 8
$2$2	$\$10$dollar sign, 10
$3$3	$\$12$dollar sign, 12
$4$4	$\$14$dollar sign, 14

Por supuesto, esta tabla solo muestra el costo total de algunos números posibles de ingredientes. Por ejemplo, no hay razón alguna que impida que tengamos $7$7 ingredientes en la pizza (¡Más allá de que sería asquerosa!).

Veamos cómo esta tabla tiene sentido para una pizza pequeña con $4$4 ingredientes.

Este es el costo de únicamente la pizza:

$\$\greenD6$dollar sign, start color #1fab54, 6, end color #1fab54

Este es el costo de los $\blueD4$start color #11accd, 4, end color #11accd ingredientes:

$\blueD4$start color #11accd, 4, end color #11accd ingredientes $\cdot$dot $\$2$dollar sign, 2 por ingrediente $=$equals $\$\goldD8$dollar sign, start color #e07d10, 8, end color #e07d10

Lo que nos lleva al costo total de

$\$\greenD6 + \$\goldD8 = \$14$dollar sign, start color #1fab54, 6, end color #1fab54, plus, dollar sign, start color #e07d10, 8, end color #e07d10, equals, dollar sign, 14.

¿Cuánto costaría una pizza pequeña con $5$5 ingredientes?

$\$$dollar sign 

[¡Necesito ayuda! Por favor, muéstrame la solución.]

$(x)$left parenthesis, x, right parenthesis	$(y)$left parenthesis, y, right parenthesis
$0$0	$\$6$dollar sign, 6
$1$1	$\$8$dollar sign, 8
$2$2	$\$10$dollar sign, 10
$3$3	$\$12$dollar sign, 12
$4$4	$\$14$dollar sign, 14
$5$5	$\$16$dollar sign, 16

$5$5$\$16$dollar sign, 16

Representación por medio de una ecuación

Escribamos una ecuación para el costo total $y$y de una pizza con $x$x ingredientes.

Este es el costo de únicamente la pizza:

$\$\greenD6$dollar sign, start color #1fab54, 6, end color #1fab54

Este es el costo de $x$x ingredientes:

$x$x ingredientes $\cdot$dot $\$2$dollar sign, 2 por ingrediente $=$equals $x \cdot 2 = \goldD{2x}$x, dot, 2, equals, start color #e07d10, 2, x, end color #e07d10

Por lo que la ecuación del costo total $y$y de una pizza pequeña es:

$y = \greenD6 + \goldD{2x}$y, equals, start color #1fab54, 6, end color #1fab54, plus, start color #e07d10, 2, x, end color #e07d10

Veamos cómo esta ecuación tiene sentido para una pizza pequeña con $3$3 ingredientes:

$x = \blueD3$x, equals, start color #11accd, 3, end color #11accd, pues hay $\blueD3$start color #11accd, 3, end color #11accd ingredientes.

El costo total es $6 + 2(\blueD3) = 6 + 6 = \$12$6, plus, 2, left parenthesis, start color #11accd, 3, end color #11accd, right parenthesis, equals, 6, plus, 6, equals, dollar sign, 12

Usa la ecuación para encontrar el costo de una pizza con $100$100 ingredientes.

$\$$dollar sign 

[¡Necesito ayuda! Por favor, muéstrame la solución.]

$x = \blueD{100}$x, equals, start color #11accd, 100, end color #11accd$\blueD{100}$start color #11accd, 100, end color #11accd

$6 + 2(\blueD{100}) = 6 + 200 = \$206$6, plus, 2, left parenthesis, start color #11accd, 100, end color #11accd, right parenthesis, equals, 6, plus, 200, equals, dollar sign, 206

Representación por medio de una gráfica

Podemos construir pares ordenados para los valores de $x$x y $y$y:

Ingredientes en la pizza $(x)$left parenthesis, x, right parenthesis	Costo total $(y)$left parenthesis, y, right parenthesis	Par ordenado $(x , y)$left parenthesis, x, comma, y, right parenthesis
$0$0	$\$6$dollar sign, 6	$(0, 6)$left parenthesis, 0, comma, 6, right parenthesis
$1$1	$\$8$dollar sign, 8	$(1, 8)$left parenthesis, 1, comma, 8, right parenthesis
$2$2	$\$10$dollar sign, 10	$(2, 10)$left parenthesis, 2, comma, 10, right parenthesis
$3$3	$\$12$dollar sign, 12	$(3, 12)$left parenthesis, 3, comma, 12, right parenthesis
$4$4	$\$14$dollar sign, 14	$(4, 14)$left parenthesis, 4, comma, 14, right parenthesis

Podemos utilizar estos pares ordenados para crear la gráfica. Cómo quedaría?

$$EeEEE

EJERCICIOS

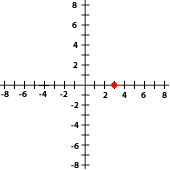
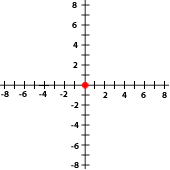
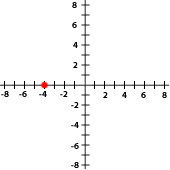
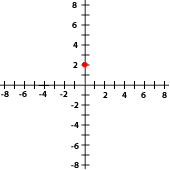
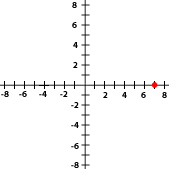
Indica las coordenadas de los puntos señalados con rojo en cada gráfica

1

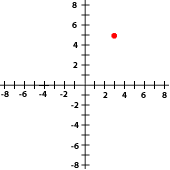
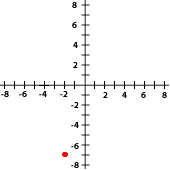
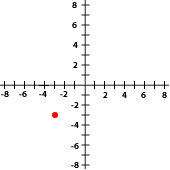
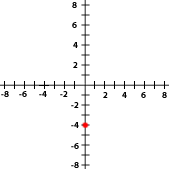
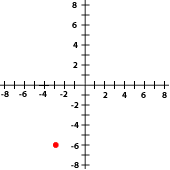
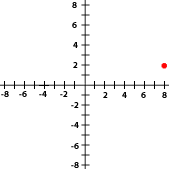
Escoge la opción correcta:

6La gráfica siguiente corresponde con el punto...

(−4,0)

(0,−4)

(−4,−4)

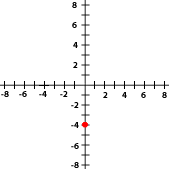
7La gráfica siguiente corresponde con el punto...

(−5,0)

(0,−5)

(5,0)

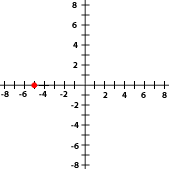
8La gráfica siguiente corresponde con el punto...

(1,0)

(1,1)

(0,1)

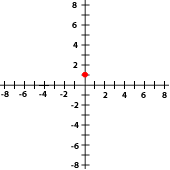
9La gráfica siguiente corresponde con el punto...

(7,0)

(7,1)

(0,7)

Varios insectos cayeron en una telaraña y se encuentran en la posición que se indica en la tabla. Considera el origen del plano cartesiano como el centro de la telaraña y ubica a los insectos.

Insectos	Posición
Mosca	(7, 9)
Avispa	(5, 2)
Mosquito	(2, 3)
Mariquita	(4, 3)
Mariposa	(8,5)
Libélula	(8, 8)

a. Si la avispa hubiera quedado atrapada 5 hilos más arriba, ¿cuáles serían sus coordenadas?
b. Escribe las coordenadas del mosquito si se hubiera atorado 3 hilos hacia la derecha.
c. ¿En qué coordenadas estaría colocada la araña si estuviera 8 hilos a la izquierda de la mosca y 4 hilos arriba

Completa las siguientes tablas según indique cada uno de los enunciados y construye su gráfica correspondiente.

1El alquiler de una moto cuesta 10 $/día. Completa la tabla que relaciona el número de días de alquiler con el precio.

Nº de días	1	2	3			10
Precio (en €)	10			60	80

2Relaciona la altura de Pedro con su edad usando los siguientes datos:
 Al año de edad medía medio metro.
 A los dos años medía 13 cm más.
 A los tres años medía 76 cm.
 A los cuatro, 87 cm.
 A los cinco le faltaban dos centímetros para llegar al metro de altura.
 A los seis, pasaba 5 cm del metro.
 Y a los siete, medía 1m y 10 cm.

Edad (en años)	1	2	3	4	5	6	7
Altura (en m)

5Completa la tabla que relaciona el lado de un cuadrado con su área.

Lado (en cm)	1	2	3			9	11
Área (en cm²)	1			36	64

-Miguel tiene en el banco ahorrados $ 1000. Decidió ahorrar $250 diarios. ¿Cuánto tendrá ahorrado al cabo de 3, 5  y 12 días?

-Desde que Renata se mudó a su nuevo hogar ha registrado la altura del árbol afuera de su ventana.

$H$H representa la altura del árbol (en centímetros) $t$t años desde que Renata se mudó.

$H=210+33t$H, equals, 210, plus, 33, t

¿Qué tan rápido crece el árbol

__________centímetros al año.

-Harry solicitó un préstamo a un banco.

$D$D representa la deuda restante de Harry (en pesos) como función del tiempo $t$t (en meses).

$D(t)=-200t+9000$D, left parenthesis, t, right parenthesis, equals, minus, 200, t, plus, 9000

¿Cuánto dinero le prestó a Harry el banco?

-La temperatura puede medirse en dos unidades comunes: grados Celsius y grados Fahrenheit.

$f$f representa la temperatura en grados Fahrenheit como función de la temperatura $c$c en grados Celsius.

$f=32+1{,}8c$f, equals, 32, plus, 1, comma, 8, c

¿Cuál es el incremento en grados Fahrenheit equivalente a un incremento de $10$10 grados Celsius?

-Andrei quiere llenar una pecera con canicas, y el espacio restante con agua.

$W$W representa la cantidad de agua (en litros) que usa Andrei si coloca $n$n canicas.

$W=32-0{,}05n$W, equals, 32, minus, 0, comma, 05, n

¿Cuál es el volumen de cada canica?