MATE 2. Semana del 3 al 6 febrero 2020
|
BLOQUE:
|
2 |
EJE:
|
Número,
álgebra y variación
|
|
TEMA:
|
Ecuaciones
|
|
SECUENCIA:
|
12.
Sistemas de ecuaciones lineales con dos incógnitas
|
|
LECCIÓN:
|
2.
Sistemas de ecuaciones lineales con dos incógnitas
|
|
APRENDIZAJES ESPERADOS:
|
•
Resuelve problemas mediante la formulación y solución algebraica de sistemas
de dos ecuaciones lineales con dos incógnitas.
|
Sistema de dos ecuaciones lineales con dos incógnitas
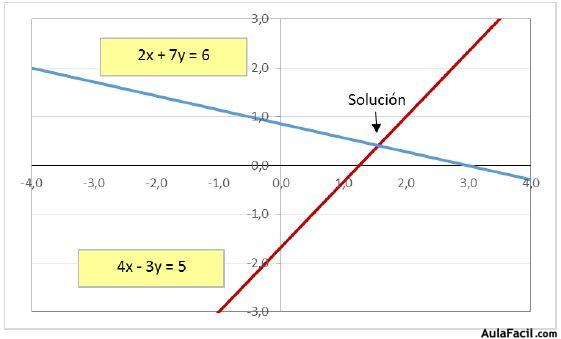
Un sistema de dos ecuaciones lineales con dos incógnitas tiene la siguiente estructura:
4x – 3y = 5
2x + 7y = 6
Cada ecuación representa una recta en el plano. La solución será el punto de corte de ambas rectas.
Solucionar este sistema de ecuaciones es encontrar los pares de valores de “x1” - “y1” que hacen cumplir ambas igualdades.
La solución de este sistema será precisamente el punto de corte de ambas rectas.
Sistemas de Ecuaciones Lineales
Para resolver un sistema de dos ecuaciones con dos incógnitas podemos utilizar uno de los siguientes métodos.
- Sustitución.
- Igualación.
- Reducción.
Resolución de Ecuaciones
Método de Sustitución
Sea el sistema
3x + y = 11
5x – y = 13
Primero en una de las ecuaciones se halla el valor de una de las incógnitas. Hallemos la y en la primera ecuación supuesto conocido el valor de x.
y=11-3x
Se sustituye en la otra ecuación el valor anteriormente hallado.
5x-(11-3x)=13
Ahora tenemos una ecuación con una sóla incógnita; la resolvemos.
5x-11+3x=13.
5x+3x=13+11.
8x=24.
x=3
Ya conocido el valor de x lo sustituimos en la expresión del valor de y que obtuvimos a partir de la primera ecuación del sistema
y=11-3x.
y=11-9.
y=2
Así la solución al Sistema de ecuaciones propuesto será x=3 e y=2
Método de igualación.
Sea el sistema
3X + Y = 11.
5X - Y = 13
Lo primero que haremos será despejar en las dos ecuaciones la misma incógnita.
y= 11 - 3x.
y= -13 + 5x.
Igualamos ambas ecuaciones. 11-3x=-13+5x.
8x=24.
x=3.
Este valor de x lo sustituímos en cualquiera de las ecuaciones de y.
y=11-9.
y=2.
Método de reducción
Sea el sistema.
3X + Y = 11.
5X - Y = 13.
Sumaremos miembro a miembro las dos ecuaciones que componen el sistema.
3x + y = 11.
5x - y = 13.
8x + 0 = 24.
8x=24
x=3 y sustituyendo este valor en cualquiera de las ecuaciones del sistema obtenemos.
y=2
Ejemplo
Sea el sistema.
3x - y = 7.
2x + 3y = 12.
5x + y = 19.
Si aplicamos el método de reducción en este caso ningún coeficiente de las variables se hace cero. Por lo tanto hay que multiplicar una de ellas por un número de forma tal que cuando sumemos una de ellas desaparezca. Por ejemplo la primera por 3.
3x – y = 7 / 3.
Obtenemos
9x - 3y = 21.
Entonces obtenemos el nuevo sistema.
9x -3y = 21.
2 x +3y = 12.
11x + 0 = 33.
11x = 33.
x=3 y sustituyendo este valor en cualquiera de las ecuaciones del sistema obtenemos.
y=2