MATE 1. Semana del 3 al 6 febrero 2020
|
BLOQUE:
|
2 |
|
EJE:
|
Número,
álgebra y variación
|
|
TEMA:
|
Proporcionalidad
|
|
SUBTEMA:
|
16.
Problemas de porcentajes
|
|
APRENDIZAJES ESPERADOS:
|
Resuelve
problemas de cálculo de porcentajes, de tanto por ciento y de la cantidad
base.
|
Porcentajes
1. Concepto de porcentaje (%)
Concepto y ejemplos de porcentaje.
Más ejemplos
El porcentaje o tanto por ciento es una forma de indicar una proporción tomando como referencia al número 100.
Escribimos el porcentaje n% (n por ciento) para referirnos a la proporción n de cada 100.
Por ejemplo, si el 40% de los alumnos de una clase son rubios, significa que por cada 100 alumnos, 40 de ellos son rubios. Pero esta no significa que haya 100 alumnos. Por ejemplo,- Si hay 100 alumnos, 40 de ellos son rubios.
- Si hay 200 alumnos, 80 de ellos son rubios.
- Si hay 50 alumnos, 20 de ellos son rubios.
Por tanto,
La cantidad que representa un tanto por ciento depende del total porque es una proporción.
2. Cálculo de porcentajes
Un porcentaje es siempre una relación de proporcionalidad directa, así que sólo tenemos que aplicar una regla de tres simple.
Explicamos dos métodos para calcular porcentajes: aplicar una regla de tres o multiplicar por un decimal.
Un porcentaje es siempre una relación de proporcionalidad directa, así que sólo tenemos que aplicar una regla de tres simple.
Explicamos dos métodos para calcular porcentajes: aplicar una regla de tres o multiplicar por un decimal.Regla de tres:
Para aplicar una regla de tres, siempre identificamos el total con el porcentaje 100%.
Ejemplo: cálculo del 25% de 324
Como 324 es el total, lo identificamos con el 100%:
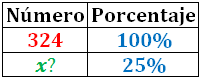 Aplicando la regla de tres, podemos calcular el valor de la incógnita x, que representa el 25% de 324:
Aplicando la regla de tres, podemos calcular el valor de la incógnita x, que representa el 25% de 324:
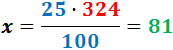 Por tanto, el 25% de 324 es 81.
Por tanto, el 25% de 324 es 81.
Regla mnemotécnica para calcular la incógnita:
Representamos dos diagonales en la tabla:
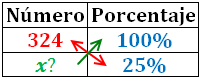 Hay una flecha que tiene un número en cada lado (la roja). Estos dos números los multiplicamos:
Hay una flecha que tiene un número en cada lado (la roja). Estos dos números los multiplicamos:
El resultado lo dividimos entre el número que apunta la otra flecha (la verde, la que tiene a la incógnita en el otro extremo):
Nota: el 25% es una cuarta parte ya que 25 es la cuarta parte de 100.
Nota 2: para obtener x hemos multiplicado 324 por 25 y dividido entre 100. Esto es lo mismo que multiplicar 324 por la fracción 25/100, es decir, multiplicar por el decimal 0,25. Esta operación es la que describimos a continuación.
Ejemplo: cálculo del 25% de 324
Como 324 es el total, lo identificamos con el 100%:
 Aplicando la regla de tres, podemos calcular el valor de la incógnita x, que representa el 25% de 324:
Aplicando la regla de tres, podemos calcular el valor de la incógnita x, que representa el 25% de 324:
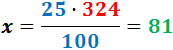 Por tanto, el 25% de 324 es 81.
Por tanto, el 25% de 324 es 81.
Regla mnemotécnica para calcular la incógnita:
Representamos dos diagonales en la tabla:
 Hay una flecha que tiene un número en cada lado (la roja). Estos dos números los multiplicamos:
Hay una flecha que tiene un número en cada lado (la roja). Estos dos números los multiplicamos:
El resultado lo dividimos entre el número que apunta la otra flecha (la verde, la que tiene a la incógnita en el otro extremo):
Nota: el 25% es una cuarta parte ya que 25 es la cuarta parte de 100.
Nota 2: para obtener x hemos multiplicado 324 por 25 y dividido entre 100. Esto es lo mismo que multiplicar 324 por la fracción 25/100, es decir, multiplicar por el decimal 0,25. Esta operación es la que describimos a continuación.
Como 324 es el total, lo identificamos con el 100%:

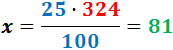
Regla mnemotécnica para calcular la incógnita:
Representamos dos diagonales en la tabla:

El resultado lo dividimos entre el número que apunta la otra flecha (la verde, la que tiene a la incógnita en el otro extremo):
Nota: el 25% es una cuarta parte ya que 25 es la cuarta parte de 100.
Nota 2: para obtener x hemos multiplicado 324 por 25 y dividido entre 100. Esto es lo mismo que multiplicar 324 por la fracción 25/100, es decir, multiplicar por el decimal 0,25. Esta operación es la que describimos a continuación.
Multiplicar por un decimal:
Vamos a explicar un método para calcular un porcentaje rápidamente. Se trata de la misma regla de tres, pero omitiendo pasos.
La operación del ejemplo anterior para calcular el 25% de 324 era
Podemos escribirla como
Es decir, multiplicamos el total (324) por un número decimal (0,25), que es la fracción 25/100. Como podemos calcular rápidamente el número decimal de un porcentaje, no hace falta escribir la tabla cada vez.
Por ejemplo,
- El 20% de es .
- El 45% de es .
- El 91,5% de es .
- El 3% de es .
La operación del ejemplo anterior para calcular el 25% de 324 era
Podemos escribirla como
Es decir, multiplicamos el total (324) por un número decimal (0,25), que es la fracción 25/100. Como podemos calcular rápidamente el número decimal de un porcentaje, no hace falta escribir la tabla cada vez.
Por ejemplo,
- El 20% de es .
- El 45% de es .
- El 91,5% de es .
- El 3% de es .
Aumentos y descuentos
En este aparto explicamos cómo calcular una cantidad final después de aplicar un aumento o un descuento.
En este aparto explicamos cómo calcular una cantidad final después de aplicar un aumento o un descuento.
Aumentos:
En el apartado 3 vimos un ejemplo en el que el precio de un cuadro subió un 50%. El precio actual se puede calcular sumando el 50% del precio inicial o calculando directamente el 150%.
Veamos otro ejemplo:
Ejemplo: Al salario de 800$ de un trabajador se le aplica un aumento del 20%. Esto quiere decir que al salario inicial le sumamos el 20%.
Calculamos el 20% de 800$:
Por tanto, el salario actual es
También, podemos obtener el sueldo actual calculando directamente el 120% de 800$ (porque 100%+20% = 120%):
En el apartado 3 vimos un ejemplo en el que el precio de un cuadro subió un 50%. El precio actual se puede calcular sumando el 50% del precio inicial o calculando directamente el 150%.
Veamos otro ejemplo:
Veamos otro ejemplo:
Ejemplo: Al salario de 800$ de un trabajador se le aplica un aumento del 20%. Esto quiere decir que al salario inicial le sumamos el 20%.
Calculamos el 20% de 800$:
Por tanto, el salario actual es
También, podemos obtener el sueldo actual calculando directamente el 120% de 800$ (porque 100%+20% = 120%):
Calculamos el 20% de 800$:
Por tanto, el salario actual es
También, podemos obtener el sueldo actual calculando directamente el 120% de 800$ (porque 100%+20% = 120%):
Descuentos:
En los descuentos o rebajas se razona del mismo modo.
Veamos un ejemplo:
Ejemplo: A un jersey de 62$ se le aplica un descuento del 10%. Esto significa que pagaremos un 10% menos del precio inicial.
Calculamos el 10% de 62$:
El precio final del jersey es de 55,8$ porque
Pagar un 10% menos es lo mismo que pagar sólo el 90% (porque 100%-10% = 90%), así que el precio final es el 90% del inicial:
Otros descuentos:
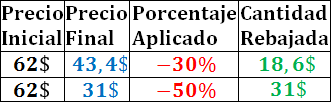 Observad que en la segunda columna están escritos el 70% y el 50% del precio inicial, que es la cantidad que pagamos. En la cuarta columna hemos escrito la cantidad rebajada: el 30% y el 50% del precio inicial (el dinero que ahorramos).
Observad que en la segunda columna están escritos el 70% y el 50% del precio inicial, que es la cantidad que pagamos. En la cuarta columna hemos escrito la cantidad rebajada: el 30% y el 50% del precio inicial (el dinero que ahorramos).
Lógicamente, cuanto mayor sea el porcentaje del descuento más decrece el precio final.
Habitualmente, se utilizan los signos ó delante de un porcentaje para señalar que es un aumento o un descuento, respectivamente. Por ejemplo,
- significa un incremento del 30%
- significa una rebaja del 30
En los descuentos o rebajas se razona del mismo modo.
Veamos un ejemplo:
Habitualmente, se utilizan los signos ó delante de un porcentaje para señalar que es un aumento o un descuento, respectivamente. Por ejemplo,Veamos un ejemplo:
Ejemplo: A un jersey de 62$ se le aplica un descuento del 10%. Esto significa que pagaremos un 10% menos del precio inicial.
Calculamos el 10% de 62$:
El precio final del jersey es de 55,8$ porque
Pagar un 10% menos es lo mismo que pagar sólo el 90% (porque 100%-10% = 90%), así que el precio final es el 90% del inicial:
Otros descuentos:
 Observad que en la segunda columna están escritos el 70% y el 50% del precio inicial, que es la cantidad que pagamos. En la cuarta columna hemos escrito la cantidad rebajada: el 30% y el 50% del precio inicial (el dinero que ahorramos).
Observad que en la segunda columna están escritos el 70% y el 50% del precio inicial, que es la cantidad que pagamos. En la cuarta columna hemos escrito la cantidad rebajada: el 30% y el 50% del precio inicial (el dinero que ahorramos).
Lógicamente, cuanto mayor sea el porcentaje del descuento más decrece el precio final.
Calculamos el 10% de 62$:
El precio final del jersey es de 55,8$ porque
Pagar un 10% menos es lo mismo que pagar sólo el 90% (porque 100%-10% = 90%), así que el precio final es el 90% del inicial:
Otros descuentos:

Lógicamente, cuanto mayor sea el porcentaje del descuento más decrece el precio final.
- significa un incremento del 30%
- significa una rebaja del 30
EJERCICIOS
Ejercicio 1
Si el precio de un artículo se rebaja en un 35%, entonces...
Pagaremos sólo el 35% del precio inicial.
| |
Pagaremos sólo el 65% del precio inicial.
| |
Pagaremos sólo el 135% del precio inicial
|
Ejercicio 2
Si el precio de una antigüedad sube un 25%, entonces...
Tendremos que pagar una cuarta parte más.
| |
Tendremos que pagar un 85% del precio inicial.
| |
Tendremos que pagar un 150% del precio inicial.
|
Ejercicio 3
Si pagamos por adelantado el 40% del precio de un artículo que ha sido rebajado, entonces
Falta por pagar un 60%.
| |
Falta por pagar un 40%.
| |
El artículo ya está pagado
|
Ejercicio 4
La fracción dos quintos (2/5 = 0,4) es el porcentaje...
2,5%
| |
0,4%
| |
40%
|
Problema 1
En un parque infantil hay 125 bolas. Calcular el porcentaje de bolas de cada color:
- Rojas: 40
- Verdes: 10
- Naranjas: 25
- Azules: 20
- Rosas: 30
Problema 2
Reescribir las siguientes proporciones en forma de porcentajes:
- Un cuarto de la población mundial vive sin electricidad.
- Sólo dos de cada cien personas en el mundo tienen los ojos verdes. Sin embargo, ocho de cada diez personas de Islandia tienen este color de ojos.
- En Rumanía, en casi la mitad de los hogares hay un gato y un perro. En Turquía, el porcentaje no llega a uno de cada diez.
Problema 3
Calcular cuánto pagaremos por un libro cuyo precio es de 25$ si le aplicamos un descuento del 25%. ¿Cuánto dinero ahorramos?
Problema 4
Después de aplicar un 30% de descuento, el precio de una computadora es de 490$. Calcular el precio inicial.
Problema 5
Ahorramos 7,05$ al aplicarle un 15% de descuento a unos pantalones. Calcular el precio inicial de los pantalones.
Problema 6
Si el número de mujeres de una población ha crecido un 20% (hay un 20% más) en un año, calcular cuántas mujeres hay ahora si antes había 2000.
Problema 7
Leemos en el cartel de una tienda que sus precios están rebajados hasta un 60%, pero el artículo que hemos comprado nos ha costado 52$ y su precio anterior era 65$. Calcular el porcentaje de la rebaja aplicada.
Problema 8
Una piscina olímpica de 2,5 millones de litros de agua está llena al 95% de su capacidad. Se calcula que se evaporará una cantidad de agua correspondiente al 5% de su capacidad total. Calcular cuántos litros se van a evaporar.
Problema 9
En una granja escuela hay caballos, vacas, gansos y pollitos. Se sabe:
- El 44% de los animales tienen cuatro patas y el resto de los animales tienen dos.
- El número de caballos es el mismo que el de gansos.
- El número de vacas es 84.
- El 40% de los animales son pollitos.
Calcular el número total de animales.
Problema 10
Tenemos 5000$ en una cuenta. A final de cada mes, se ingresa un 5% del dinero que hay en la cuenta en dicho momento. Calcular el dinero que habrá en la cuenta después de un trimestre (3 meses). ¿En qué porcentaje ha subido la cantidad inicial?
Problema 11
En una empresa automovilística, las ganancias del año pasado fueron 123 millones. Según las estadísticas, en el año actual, las ganancias van a reducirse en un 115% con respecto al año anterior. Calcular las ganancias que habrá este año.