MATE 3. Semana del 2 al 6 diciembre 2019

Bloque:	2
Eje:	Forma, espacio y medida
TEMA:	Medida
APRENDIZAJES ESPERADOS	• Explicitación y uso del teorema de Pitágoras.

 Explicitación y uso del teorema de Pitágoras

.

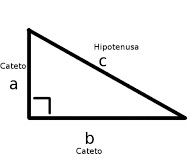
Teorema de Pitágoras

Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos: Si el triángulo rectángulo (tiene un ángulo recto (90°)) ... y pones un cuadrado sobre cada uno de sus lados, entonces... ... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos! En teorema afirma: "En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos" Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²): a2 + b2 = c2  Para entender más fácilmente Demostración Aritmética: Consiste en sumar las áreas de los cuadros formados en los lados de un triangulo rectángulo. Demostración geométrica: Se forman los cuadrados a partir de los lados de un triangulo rectángulo (ACB) y se cortan los cuadrados formados de los catetos, identifica que se pude sobre poner en el cuadro de la hipotenusa y no sobra absolutamente nada:

Utilidad del teorema de Pitágoras

Encontrando la Longitud de la Hipotenusa

Podemos usar el Teorema de Pitágoras para encontrar la longitud de la hipotenusa de un triángulo rectángulo si conocemos la longitud de sus catetos. Es decir, si conocemos las longitudes de a y b, podemos encontrar c.

Hagámoslo.

Encontrando la Longitud de un Cateto

Podemos también usar el Teorema de Pitágoras para encontrar la longitud de uno de los catetos de un triángulo rectángulo si nos dan las medidas de la hipotenusa y del otro cateto. Considera el triángulo siguiente:

Ejemplos

1) Una ciudad se encuentra 17 km al oeste y 8 km al norte de otra. ¿Cuál es la distancia real lineal entre las dos ciudades?

 Lo primero es realizar un pequeño dibujo que nos permita identificar la situación y ver cómo definimos un triángulo rectángulo en la misma.

Este podría ser un buen dibujo, donde observamos que se cumplen los datos que nos da el problema y que además la distancia real entre las ciudades, vendría a ser la hipotenusa de nuestro triángulo rectángulo.

El triángulo entonces queda claramente definido y sabemos que tenemos un cateto que mide 17 km, otro que mide 8 km y que la distancia real que se nos está pidiendo es la hipotenusa del tal triángulo. Aplicamos Teorema de Pitágoras y el planteo sería así:

a² = b² + c²
a² = 8² + 17² = 64 + 289 = 353
 a = √353 = 18.8

Respuesta final: la distancia real entre las dos ciudades es de 18,8 km

2) Una escalera cuya longitud es de 3 metros  se encuentra apoyada contra una pared en el suelo horizontal y alcanza 2,8 m sobre esa pared vertical. La pregunta es: ¿a qué distancia está al pie de la escalera de la base de la pared?

 

En este caso, el dibujo que podemos hacer para interpretar la letra del problema sería algo como esto, donde nuevamente se identifica sin problemas el triángulo rectángulo.

Queda claro que la escalera cumple el rol de la hipotenusa, la altura de la pared (dato conocido) es uno de los catetos y la distancia del pie de la escalera hasta la base de la pared, es el otro cateto, precisamente la medida que se nos pide calcular y que como es una incógnita para nosotros hemos llamado “x”.

El planteo de resolución en este caso podría ser el siguiente:

a² = b² + c²
3² = b² + 2.8² 
 9 =  b² + 7.84
b² = 9 – 7.84 = 1.16
b = √1.16 = 1.08

Respuesta final: el pie de la escalera está a 1,08 mt de la pared.

3) Una cáncha de fútbol (rectangular como sabemos)  mide 125 metros de largo. Si la longitud de sus diagonales es de 150 metros. ¿cuál es el ancho del campo de juego?

 Analizando la figura, vemos que el triángulo queda comprendido por esa diagonal del campo de juego (la hipotenusa), el largo del campo (uno de los catetos) y el ancho (el otro cateto cuya longitud es  lo que se nos pide hallar). El planteo de resolución sería el siguiente:

 a²         =  b² + c²
150²     = 125² + c² 
22,500  = 15,625 + c² 
         c² = 22,500 – 15,625 = 6,875
         c  = √6,875

          c = 82.9

Respuesta final: el ancho del campo de fútbol es de 82,9 metros

Sumario

El Teorema de Pitágoras nos dice que para cualquier triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, El teorema está representado por la fórmula 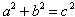.  Si conocemos las longitudes de dos de los lados del triángulo, podemos aplicar el Teorema de Pitágoras para encontrar la longitud del tercer lado.

EJERCICIOS
1.

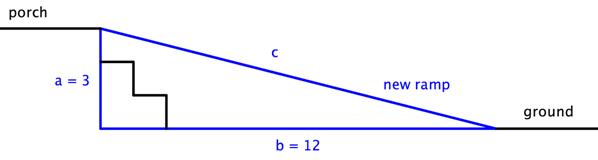
Los propietarios de una casa quieren convertir a una rampa los escalones que llevan del suelo al porche. El porche está a 3 pies sobre el suelo, y debido a regulaciones de construcción, la rampa debe empezar a 12 pies de distancia con respecto al porche. ¿Qué tan larga debe ser la rampa?

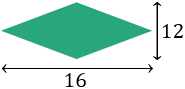
2. Calcular el perímetro del siguiente rombo si sabemos que sus diagonales (altura y anchura) miden 16 y 12.

3. Calcular la altura que podemos alcanzar con una escalera de 3 metros apoyada sobre la pared si la parte inferior la situamos a 70 centímetros de ésta.

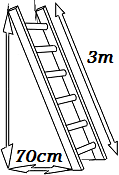
Ver solución

Problema 4

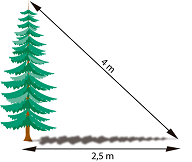
Al atardecer, un árbol proyecta una sombra de 2,5 metros de longitud. Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de 4 metros, ¿cuál es la altura del árbol?

Problema 5

La medida que se utiliza en los televisores es la longitud de la diagonal de la pantalla en unidades de pulgadas. Una pulgada equivale a 2,54 centímetros:

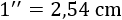
Si David desea comprar un televisor para colocarlo en un hueco de 96x79cm, ¿de cuántas pulgadas debe ser el televisor?

Problema 6

Un clavadista está entrenando en una piscina con una plataforma. Cuando realiza el salto, cae a una distancia de 1 metro de la plataforma sumergiéndose 2,4 metros bajo el agua. Para salir a la superficie, bucea hasta el final de la piscina siguiendo una línea transversal de 8,8 metros de longitud.

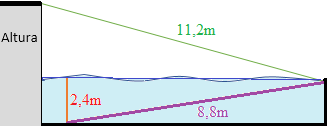
Si la longitud desde la parte superior de la plataforma al lugar en donde emerge del agua es de 11,2 metros, ¿cuál es la altura de la plataforma (desde el nivel del agua)?

7. Para aplicar el teorema de Pitágoras...

	Es necesario tener un ángulo obtuso.
	Es necesario tener un ángulo recto.
	Es necesario tener un triángulo equilátero.
	Todas las opciones anteriores son falsas.

8. En un triángulo rectángulo de lados 1cm y 1dm, ¿cuánto mide la hipotenusa?

	$$\sqrt{101}cm$$
	$$\sqrt{202}cm$$
	$$\sqrt{101}dm$$
	Todas las opciones anteriores son falsas.

9. La siguiente figura está compuesta por dos rectángulos (uno azul y uno amarillo) y un triángulo equilátero (todos sus lados miden lo mismo).

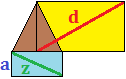
Sabemos que uno de los lados y la diagonal del rectángulo azul miden:

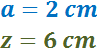
Se desea calcular cuánto mide la diagonal del otro rectángulo (d) aplicando el teorema de Pitágoras.

	No es posible calcular la diagonal con los datos que conocemos.
	Es posible calcularla y mide 7.5cm.
	Es posible calcularla y mide 11cm.
	Ninguna de las opciones anteriores es cierta.

10. LA DIAGONAL DE UN CUADRADO DE ÁREA 1 CM2 MIDE...

	$$1cm$$
	$$1dm$$
	$$\sqrt{2}cm$$
	$$\sqrt{3}dm$$

 

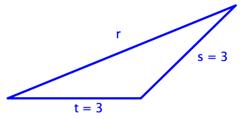
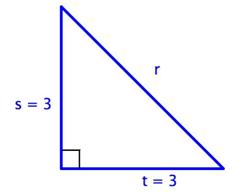
¿Para cuál de los siguientes triángulos es ? A)  B)  C)  D)