MATE 3. Semana del 28 enero al 1º febrero 2019

Bloque:	3
Eje:	Forma, espacio y medida
TEMA:	Figuras y cuerpos
SUBTEMA	• Resolución de problemas geométricos mediante el teorema de Tales.
APRENDIZAJES ESPERADOS	• Resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.

TEOREMA DE THALES

Si dos rectas cualesquiera se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.

     

Ejemplos

1 Las rectas a, b y c son paralelas. Halla la longitud de x.

2 Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?

Sí, porque se cumple el teorema de Thales.

Teorema de Thales en un triángulo

Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.

     

Ejemplo:

Hallar las medidas de los segmentos a y b.

Aplicaciones del teorema de Thales

El teorema de Thales se utiliza para dividir un segmento en varias partes iguales.

Ejemplo:

Dividir el segmento AB en 3 partes iguales.

1 Se dibuja una semirrecta de origen el extremo A del segmento.

2 Tomando como unidad cualquier medida, se señalan en la semirrecta 3 unidades de medida a partir de A

3 Por cada una de las divisiones de la semirrecta se trazan rectas paralelas al segmento que une B con la última división sobre la semirrecta. Los puntos obtenidos en el segmento AB determinan las 3 partes iguales en que se divide.

TAREA PARA ENTREGAR EL VIERNES 1º

Señala la opción correcta:

1Para poder aplicar el teorema de Thales necesitamos...

dos rectas cualesquiera y varias rectas paralelas entre sí que corten a las anteriores.

dos rectas paralelas y varias rectas cualesquiera que cortan a las anteriores.

dos rectas cualesquiera y varias rectas paralelas entre sí que pueden serlo o no a las anteriores.

2Una de las aplicaciones del teorema de Thales es...

dividir un segmento en varias partes iguales.

formar un segmento a partir de varias de sus partes.

Las dos respuestas anteriores son correctas.

3Podemos aplicar el teorema de Thales en triángulos cuando...

trazamos rectas paralelas a alguno de sus lados.

trazamos rectas perpendiculares a alguno de sus lados.

trazamos rectas paralelas a alguno de sus lados que intersequen a los otros dos lados del mismo.

4Sabiendo que las rectas r, s y t son paralelas, la longitud de x es

2.5 cm

3 cm.

No se puede calcular.

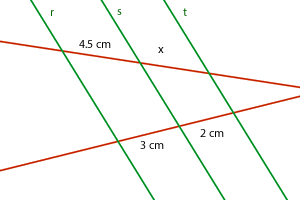
5Sabiendo que las rectas r, s y t son paralelas, las longitudes que faltan son:

x = 2.625 cm, y = 10 cm.

x = 10 cm, y = 2.625 cm.

Faltan datos para resolver el problema.

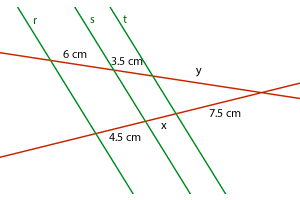
6Sean a y b dos rectas cualesquiera y r y s dos rectas que las cortan. Si los segmentos que determinan a y b son m = 5.5, n = 4, m' = 2.5 y n' = 2 entonces...

r y s son paralelas. 

r y s no son paralelas.

r y s son perpendiculares.

7Sabiendo que el segmento DE es paralelo a la base del triángulo, las medidas de los segmentos a y bson...

a = 8 cm y b = 10 cm.

a = 9 cm y b = 11 cm.

Ninguna de las respuestas anteriores es correcta.

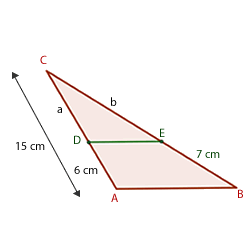
8Sabiendo que los segmentos que miden 3 cm y 4 cm son paralelos, calcular a y b.

a = 3 cm y b = 0.5 cm.

a = 3 cm y b = 1.6 cm.

a = 3.5 cm y b = 0.6 cm.

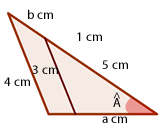
Resuelve los siguientes problemas:

9¿Cuál es la altura del montón de libros situado sobre el césped?

 cm

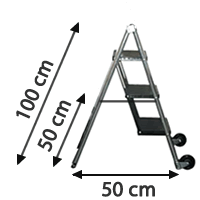
10Observando la escalera que aparece en el dibujo calcula la longitud de la cuerda que une los peldaños de la escalera con su parte posterior.

¿Cuál es la distancia entre el chico y la base de la torre (el chico ve la torre reflejada en el agua)?

El bañista se encuentra a 5 metros del barco. La borda del barco está a 1 metro sobre el nivel del mar. El mástil del barco sobresale 3 metros de la borda. El bañista ve alineados el extremos del mástil y el foco del faro.

¿A qué altura sobre el nivel del mar se encuentra el foco del faro?

Ejercicio 6

¿A qué altura se encuentra el extremo superior de la escultura, sabiendo que Paula la ve alineada con el borde de la valla?

Examen tipo PLANEA

1.    Un edificio en forma de prisma rectangular ocupa un volumen de 7 500 m3, ¿cuánto mide el ancho de su base (x) si su altura mide 25 m y el frente mide 20?

A) 15 m	C) 130 m
B) 25 m	D) 375 m

 

2.      El ingreso de Ramón es directamente proporcional al tiempo que labora, ¿cuál de las siguientes gráficas representa lo que gana en función de las horas que trabaja?

Considera el pago como de $5.00 por hora.

	y											y
	Ingreso ($)  25										Ingreso ($)  25
	20										20
	15										15
A)	10									C)	10
	5										5
										x														x
	Tiempo (hrs)											Tiempo (hrs)
			1  2  3  4  5											1		2		3		4		5
	y											y
	Ingreso ($)  25										Ingreso ($)  25
B)	20									D)	20
	15										15
	10										10
	5									x	5													x
	Tiempo (hrs)
			1  2  3  4  5									Tiempo (hrs)		1		2		3		4		5

3.      La suma de las estaturas de Rosa, Julia y Lucero es de 4.5 m. La estatura de Rosa es 1.49 m y la de Julia 1.46 m. ¿Cuál es la estatura de Lucero?

A) 1.10 m	C) 1.65 m
B) 1.55 m	D) 1.73 m

4.      Ángel y Luis se observan mutuamente desde diferentes lugares, tal como se muestra en la figura. Los ángulos formados con la horizontal y la línea de mira se llaman ángulo de elevación (α) y de depresión (β), respectivamente. ¿Cuál es la medida del ángulo de elevación (α) que tiene Luis?

A) 54°	C) 120°
B) 90°	D) 126°

5.  Observa el corte que se le hizo a un cono con el plano que se muestra:

 

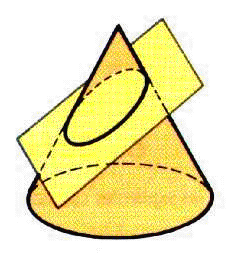
¿Cuál de las siguientes figuras se forma en la intersección del cono con el plano?

A) circunferencia          C) elipse

B) parábola                  D) hipérbola