MATE 2: Semana del 28 enero al 1º febrero 2019

BLOQUE	2
EJE:	Forma, espacio y medida
TEMA:	Medida
Subtema	• Justificación de las fórmulas para calcular el volumen de cubos, prismas y pirámides rectos
APRENDIZAJES ESPERADOS:	• Resuelve problemas en los que sea necesario calcular cualquiera de las variables de las fórmulas para obtener el volumen de cubos, prismas y pirámides rectos. Establece relaciones de variación entre dichos términos.

1. Volumen y capacidad

Unidades de volumen
Una unidad de volumen es 1000 veces mayor que la del orden inmediato inferior y 1000 veces más pequeña que la del orden inmediato superior.

Capacidad y volumen
El volumen es la cantidad de espacio que ocupa un cuerpo y capacidad es lo que cabe dentro de un recipiente. En general se llama capacidad de un recipiente a su volumen.

Relación entre las unidades.
Cada unidad de volumen es 1000 veces mayor que la del orden inferior siguiente y 1000 veces menor que la del orden superior anterior. Para pasar de una unidad a otra basta con observar cuántos niveles se suben o se bajan. Multiplicaremos por mil tantas veces como niveles se bajen y dividiremos entre mil tantas veces como niveles se suban. Por ejemplo: para pasar de hm3 a m3 hay que bajar dos niveles, lo que equivale a multiplicar por 1000 dos veces, que es igual que multiplicar por 1.000.000. En general se llama capacidad de un recipiente a su volumen. Tanto las unidades de volumen, como los múltiplos y divisores del litro, se usan para medir volúmenes y capacidades.

2. Volúmenes de prismas y pirámides Cubo Un cubo es un prisma particular formado por seis caras cuadradas. Su volumen es el cubo de la longitud de la arista. Ortoedro Un ortoedro es un prisma cuyas caras son todas

Recordemos antes los elementos del prisma.

Área y volumen de un prisma.

Para calcular el área total de un prisma siempre es necesario conocer tres medidas:

1. El área de una base.
2. El perímetro de la base
3. La altura del prisma

Las fórmulas generales para obtener el área y el volumen de cualquier prismason las siguientes:

El volumen de un octaedro (u octoedro) se calcula mediante la fórmula siguiente:

CUERPO GEOMÉTRICO	VOLUMEN	FÓRMULA
PRISMA	Área de la base por altura			Ábxh
PIRÁMIDE	Un tercio del área de la base por altura			Ábxh
		3
CUBO	La arista al cubo			a³
CILINDRO	Área de la base por altura		π r² xh
CONO	Un tercio del área de la base por la altura		π r² x h
		3
ESFERA	Cuatro tercios de pi por el cubo del radio	4/3 π x rᶟ

TAREA PARA ENTREGAR EL VIERNES 1º

1. Layla quiere construir una caja de madera que tenga un volumen de $45$ centímetros cúbicos. Empezó con un ancho de $3\text{ cm}$ y una altura de $3\text{ cm}$.

¿Cuál debe ser el largo de la caja?

 $\text {cm}$

2. Bruce compró una enorme caja de jugo que se muestra a continuación. Planea beber $630$ centímetros cúbicos de jugo cada día.

¿Cuántos días le llevará a Bruce beber toda la caja de jugo?

Escoge 1 respuesta:

Escoge 1 respuesta:

• $1$ día
• $4$ días
• $7$ días
• $10$ días

$10 \dfrac12 \text{ cm}$$20 \text{ cm}$$30 \text{ cm}$

3. El joyero de Camila tiene un volumen de $36$ centímetros cúbicos.

¿Cuáles de las siguientes podrían ser las dimensiones del joyero de Elaine?

Elige todas las respuestas adecuadas:

Elige todas las respuestas adecuadas:

• $12\text{ cm}$ de largo, $12\text{ cm}$ de ancho, $12\text{ cm}$ de alto
• $3\text{ cm}$ de largo, $4\text{ cm}$ de ancho, $3\text{ cm}$ de alto
• $4\text{ cm}$ de largo, $4\text{ cm}$ de ancho, $2\text{ cm}$ de alto

4. Lizz quiere conocer el volumen de su anillo de oro en centímetros cúbicos. Consigue un vaso con una base rectangular de 

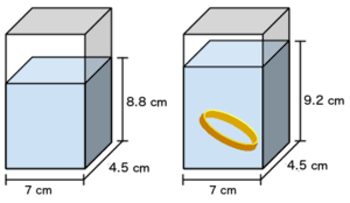
$7\text{ cm}$ por $4.5\text{ cm}$ y llena el vaso con agua a una altura de $8.8\text{ cm}$. Laura deja caer su anillo en el vaso y mide la nueva altura del agua, que es $9.2\text{ cm}$.

¿Cuál es el volumen en centímetros cúbicos del anillo de Laura?

$\qquad$

 $\text{cm}^3$

5.

La familia González se está mudando y necesita una camión con al menos $55$ metros cúbicos de capacidad. Los camiones de mudanzas entre los que han escogido se muestran en la tabla de abajo.

¿Cuál es el camión más pequeño que pueden usar?

Escoge 1 respuesta:

Escoge 1 respuesta:

• Camión pequeño
• Camión mediano
• Camión grande

Dimensiones de los camiones de mudanzas

	Largo $\text{(m})$	Ancho $\text{(m})$	Alto $\text{(m})$
Camión pequeño	$3 \dfrac13$	$2$	$2$
Camión mediano	$5$	$2 \dfrac23$	$3$
Camión grande	$7$	$3$	$3 \dfrac23$

6. La alberca de Santiago contiene 

$270$ metros cúbicos de agua. La base de la alberca mide $15\text{ m}$ de largo y $9\text{ m}$ de ancho.

¿Cuál es la altura del agua de la alberca de Santiago?

 $\text {m}$

7. Medir la caja del inodoro de tu casa y calcular el volumen de  la misma. Cuánta agua utilizas al día en tu casa  incluyendo a tu familia?

8. Calcula, por tanteo, la longitud de la arista de un cubo de 343 m3 de volumen.

 La arista medirá 7 m, ya que: 7 · 7 · 7 = 343 m3 5.

9. Halla el peso de un bloque cúbico de hormigón de 1,9 m de lado. (Un metro cúbico de hormigón pesa 2350 kg)  El volumen del bloque es: V= (1.9)3 = 6 859 m3 Su peso será: m= 2350 · 6 859 = 16 118 7 Kg.

10. ¿Cuántos peces, pequeños o medianos, se pueden introducir en un acuario cuyas medidas interiores son 88 x 65 x 70 cm? (Se recomienda introducir, a lo sumo, un pez mediano o pequeño cada cuatro litros de agua)

11. La Gran Pirámide de Giza es la única que perdura de las siete maravillas del mundo antiguo. Actualmente tiene una altura de 137 m y la base es un cuadrado de 230 m de lado. ¿Cuál es su volumen aproximado?

12. Las dimensiones de un paquete de leche son 19.2 cm, 5.9 cm y 9 cm. El fabricante quiere cambiar el envase reduciendo el área de la base un 15% y aumentando la altura un 10%. Calcular el volumen del nuevo envase redondeando a dos cifras decimales.

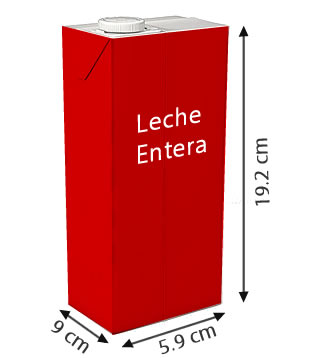
  m³

¿El nuevo envase traerá menos leche?

Si el precio del paquete es de 0.90 € y se venden 95000 litros de leche al mes, ¿Cuánto gana la empresa con el nuevo envase?

13. Marta tiene una colección de minerales. Uno de sus favoritos es la fluorita (el cual tiene forma de octaedro) que podemos observar en el siguiente dibujo:

Sabiendo que su arista mide 1.3 cm, calcula el volumen de esta pieza de colección.

 

V =  cm³