MATE 3. Semana del 23 al 27 septiembre 2019
EJE:
|
Análisis de datos |
TEMA:
|
Proporcionalidad y funciones
|
SUBTEMAS:
|
4. Representaciones de una misma situación
|
CONTENIDO:
|
• Análisis de representaciones (gráficas, tabulares y algebraicas)
que corresponden a una misma situación. Identificación de las que
corresponden a una relación de proporcionalidad.
|
APRENDIZAJES ESPERADOS
|
• Explica la diferencia entre eventos complementarios, mutuamente
excluyentes e independientes.
• Explica el tipo de transformación (reflexión, rotación o traslación) que se aplica a una figura para obtener la figura transformada. Identifica las propiedades que se conservan. |
Qué tanto sabemos de proporciones
• Revisemos qué tanto recuerdas sobre proporcionalidad y su representación en una gráfica cartesiana.
Pero para entrar a revisar un ejercicio revisemos los elementos de un plano cartesiano.
Ejemplifiquemos…
• Si acompañan a su mamá a comprar refrescos, ¿qué determina cuánto van a pagar? Si cada refresco costara $2.5, ¿cuánto pagarían por comprar tres? ¿Por qué se dice que una variación es proporcional? ¿Cómo representaríamos estos datos en un plano cartesiano?
Seguimos encontrando pistas…
• Podemos representar estos datos en una tabla
Cantidad
|
Costo
|
1
|
2.5
|
2
|
5.0
|
3
|
7.5
|
4
|
10
|
5
|
12.5
|
Ahora sólo nos falta graficar estos datos en un plano cartesiano.
Aplicando lo aprendido…
• Con base en la gráfica de la travesía de una moto de carreras que va a una velocidad constante y se encuentra en determinado momento en el punto A (abscisa 20, ordenada 50) contesten las siguientes preguntas:
Encuentra el valor faltante en las tabulaciones.
• En equipos resuelvan el siguiente problema:
• Un automóvil viaja a una velocidad constante, algunas distancias y tiempos de recorrido se muestran en la tabla. Completa los datos que hacen falta en ella y contesta las preguntas.
Tiempo (h)
|
1.5
|
3
|
5
| |
Distancia
(km)
|
240
|
720
|
Concluyendo…
• Cuál es la constante de proporcionalidad?___________
• ¿Cuál de las siguientes expresiones d = 40t; d= 80t; d= 120t es la que corresponde? ___________________________
• Argumenten su respuesta _________________________
• Con base en la expresión algebraica identificada, calculen la distancia recorrida por el automóvil en:
• a) 10 horas ________________________________
• b) 12 horas y media ______________________________
Imagina que estás con tu prima de 6 años en el zoológico una tarde de verano. Ella está en la edad en la que insiste en contar todo lo que ve. Mientras van caminando por el estacionamiento, ella quiere contar todas las llantas de los carros. Es tierno, pero se pierde mucho tiempo, por lo que le enseñas un truco que ella puede usar. Puede contar sólo el número de carros y luego multiplicar por 4 porque el número de llantas está relacionado de forma predecible al número de carros. Ella piensa que eso es divertido, y por fin logran entrar al zoológico.
Ahora tu sobrina decide que quiere contar todas las patas de los animales. ¿Es posible agilizar las cosas diciéndole que sólo cuente las cabezas y luego multiplique por una cantidad fija para obtener el número de patas? No, porque animales distintos tienen distinto número de patas — los leones tienen 4 patas, los flamencos tienen 2, y las serpientes no tienen ninguna. Al aumentar el número de animales, el número de patas no aumenta en un patrón fijo o predecible. Suspiras y te compras una bolsa extra grande de palomitas para pasar el tiempo.
Estas dos situaciones son relaciones — cada una de ellas tiene una variable de entrada independiente (el número de carros o el número de animales) y una variable de salida dependiente (el número de llantas o de patas). Pero la primera relación es un ejemplo de una clase especial, llamada función proporcional. Una función es proporcional cuando la salida es igual a la entrada multiplicada por una constante. El número de llantas es igual al número de carros multiplicado por 4. Si no hay carros en el estacionamiento, entonces el número de llantas es 4 por 0, o 0. Si hay 3 carros, el número de llantas es 4 por 3. Si hay 10 carros, hay 4 veces 10 llantas.
En cualquier función, una cantidad es dependiente de la otra. En el ejemplo del carro, el número de llantas depende del número de carros en el estacionamiento. Algebraicamente, podemos representar ésta relación con una ecuación.
llantas = 4 • carros
El número 4 nos describe cómo es la relación entre el número de carros y el número de llantas. Todas las funciones proporcionales funcionan de la misma manera. Llamamos a esa proporción constante de variación, o constante de proporcionalidad. Es una constante porque éste número no cambia dentro de la función. Como la entrada y la salida están ligadas por una constante, cambios en la variable independiente causan un cambio proporcional en la variable dependiente en una forma constante. Ésta relación proporcional le da su nombre a las funciones proporcionales.
Podemos utilizar la ecuación de los carros y las llantas como base para escribir una ecuación algebraica general que funcionará para todas las funciones proporcionales. En nuestro ejemplo, las llantas son la salida, 4 es la constante, y los carros son la entrada. Pongamos éstos términos genéricos en la ecuación. Obtenemos salida = constante • entrada. Ésa es la fórmula para todas las funciones proporcionales.
llantas = 4 • carros
salida = constante • entrada
Cambiémosla de una fórmula verbal a una simbólica — será más rápido de escribir. La salida de una función es también conocida como la variable dependiente y es generalmente representada simbólicamente como y. La entrada se llama variable independiente, representada por el símbolo x. Representemos la constante con la letra k. Ahora pondremos esos símbolos en la ecuación.
llantas = 4 • carros
salida = constante • entrada
y = kx
¡Y lo hemos logrado! Todas las funciones proporcionales se pueden describir con la ecuación y = kx.
¿Cuáles de las siguientes ecuaciones representan funciones proporcionales?
Ecuación 1: 
Ecuación 2: 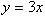
Ecuación 3: 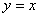
Ecuación 4: 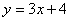
A) La Ecuación 1
B) Las Ecuaciones 2 y 3
C) La Ecuación 4
D) Las Ecuaciones 2 y 4
Funciones Proporcionales en Tablas y Conjuntos de Pares Ordenados
Como otras funciones, las funciones proporcionales pueden ser descritas y exploradas usando tablas y conjuntos de pares ordenados. Veamos cómo las tablas de funciones proporcionales pueden ser útiles.
Mary trabaja en un puesto cerca de la granja familiar, vendiendo huevos a $1.99 por cartón los fines de semana. Cuando los clientes compran muchos cartones, ella tiene que sumar los totales con lápiz y papel, y le preocupa cometer errores. Por suerte, ésta es una relación proporcional — la salida (costo total) es igual a la entrada (número de cartones) multiplicada por una constante (el precio por cartón). Mary puede usar una función proporcional para obtener una tabla de precios.
Número de cartones
|
Precio total
|
Ahora sólo tiene que utilizar la ecuación para calcular los valores y llenar la tabla. Recuerda, la ecuación de la función proporcional es y = kx. Por lo que en éste caso, costo total = precio del cartón • número de cartones. Costo total = 1.99 • número de cartones.
¿Cuál es la constante de la función mostrada en la tabla?
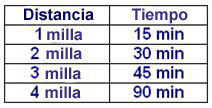
A) 15
B) 1
C) Distancia
D) Tiempo
Funciones Proporcionales en Gráficas
Cuando las funciones proporcionales son graficadas, muestran algunas características distintivas — todas las funciones proporcionales son una línea recta que pasa a través del origen.
Grafiquemos la función costo/cartón que hemos estado discutiendo.
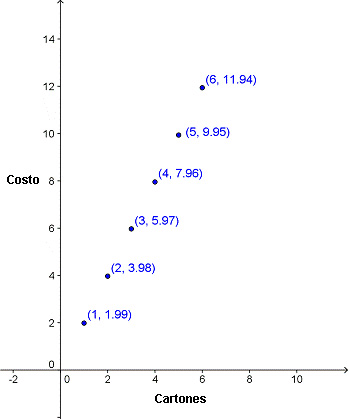
Ésta es una función discreta — está hecha de puntos individuales, porque el puesto de la granja sólo vende cartones de huevo completos. Pero podemos ver que todos los puntos están espaciados de manera uniforme, y aparentemente forman una línea recta. También podemos ver que a pesar de no estar graficado, el punto (0,0) satisface la función — el costo de 0 cartones sería de $0.
Ahora veamos la gráfica de una función proporcional continua para ver cómo se comparan. Imagina un grifo que vierte agua en una tina a un ritmo de 2.5 galones por minuto. La cantidad de agua en la tina varía directamente con la cantidad de tiempo que el grifo ha estado abierto. Podemos representar ésta relación entre el tiempo y el agua en la tina con la siguiente fórmula:
Total de galones = 2.5 galones/minuto • tiempo en minutos
Usando g para representar el total de galones de agua y t para representar el tiempo, podemos abreviar ésta relación como g = 2.5t, la cual se ve muy familiar a la fórmula estándar de funciones proporcionales, y = kx.
Construyamos una tabla para representar la relación entre el tiempo y la cantidad de agua en la tina. Después de 1 minuto, hay 2.5 galones en la tina. En 2 minutos, el total es 5 galones, y así sucesivamente. Para encontrar la cantidad total de agua en la tina en cualquier momento, podemos multiplicar el tiempo por 2.5 galones por minuto. Seis minutos nos dan suficiente puntos para crear una tabla que nos sirva.
Tiempo
|
Total de galones
|
1
|
2.5
|
2
|
5.0
|
3
|
7.5
|
4
|
10.0
|
5
|
12.5
|
6
|
15.0
|
Ahora podemos graficar esos puntos.
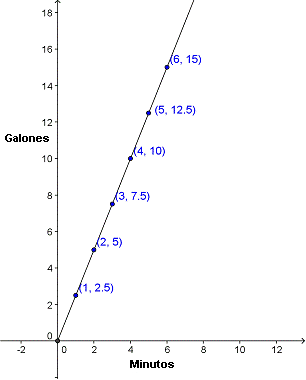
Ésta vez trazaremos una línea que conecte a los puntos, ya que el tiempo y el agua se incrementan continuamente. Y mira — los puntos quedan en una línea recta que inicia en el origen y se levanta en con un ángulo constante, justo como la gráfica anterior. Cuando las variables en una función cambian con un ritmo o una tasa constante como ésta, tienen una relación proporcional. Ésta tasa de cambio constante se llama constante de variación.
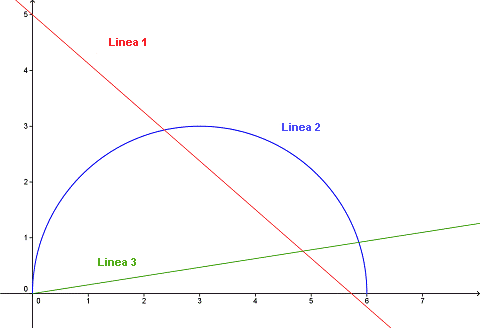
¿Cuál línea es una función proporcional?