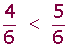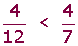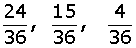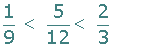MATE 1. Semana del 9 al 13 septiembre 2019

Los signos que se utilizan para mostrar que una fracción  o un número es mayor, menor o igual a otra son los siguientes.

Orden y comparación de números decimales 

1- Relaciones de orden entre números decimales
Para comparar números decimales puedes comparar las partes enteras de los números decimales entre sí y luego las cifras decimales según su posición, comenzando por la de mayor valor ( décimos), hasta que una de ellas sea de menor  o mayor que la otra.
Por ejemplo, comparar 4,25 y 4,21

 

Otro caso es cuando tenemos números decimales, con distintas cantidades de cifras decimales después de la coma.
Para comparar si un número decimal es mayor, menor o igual a otro podemos igualar con ceros las cifra decimales para que cada cantidad tenga el mismo número de cifras decimales después de la coma.
Ya igualadas las cifras procedemos a comparar y a ubicar en la posición que le corresponde.

En el siguiente ejemplo queremos saber Cuál número es mayor entre 0,2 y 0,85. Observa en la gráfica que lo primero que se hace es igualar el número de cifras decimales agregando ceros a la derecha, para luego poder compararlas.

 

Orden en las fracciones

Con igual denominador

De dos fracciones que tienen el mismo denominador es menor la que tiene menor numerador.

Con igual numerador

De dos fracciones que tienen el mismo numerador es menor el que tiene mayor denominador.

Orden con numeradores y denominadores distintos

En primer lugar las tenemos que poner a común denominador.

Es menor la que tiene menor numerador.

Común denominador

Reducir varias fracciones a común denominador consiste en convertirlas en otras equivalentes que tengan el mismo denominador.

Para la reducción de fracciones a común denominador seguiremos los siguientes pasos:

1º Determinamos el denominador común, que será el mínimo común múltiplo de los denominadores.

2º El denominador común, se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.

Ejemplos

Poner a común denominador los siguientes grupos de fracciones:

1. 

Descomponemos en factores los denominadores

3 = 3

12 = 2² · 3

9 = 3²

m.c.m.(3, 12, 9) = 2² ·3² = 36

El común denominador será 36

Dividimos 36 entre 3 y lo multiplicamos por 2

Dividimos 36 entre 12 y lo multiplicamos por 5

Dividimos 36 entre 9 y lo multiplicamos por 1

2. 

m.c.m.(5, 3, 10) = 2 · 3 · 5 = 30

3. 

m.c.m.(3, 4, 6) = 2² · 3 = 12

TAREA PARA ENTREGAR EL JUEVES 12 

1. Ordena los números de menor a mayor.
Pon el número más pequeño a la izquierda y coloca el signo 

donde corresponda de las series de tres cantidades

1.

• $111115{,}42$5, comma, 42
• $5{,}024$5, comma, 024
• $5{,}042$5, comma, 042

2.

• $3$3
• $0{,}39$0, comma, 39
• $0{,}33$0, comma, 33

3. 

• $8{,}283$8, comma, 283
• $8{,}23$8, comma, 23
• $8{,}289$8, comma, 289

4. 

• $1{,}001$1, comma, 001
• $0{,}113$0, comma, 113
• $1{,}101$1, comma, 101

5. 

             35.48       37.85    39.0


6. 

             1/2    3/4       3/8

7. 

            1/3    2/6      3/9

8.          3/7     3/9

9.         2/5     6/5

10.      3/9     3/4

11.      5/12      2/15       5/4        7/5

12. Ania, Camila y Samantha  compran un refresco cada una. A los diez minutos le queda la mitad a Ania, tres cuartos a Camila y un tercio a Samantha. Ordena de menor a mayor a las tres amigas, seg'un la cantidad que les quede.

13. Ordena de mayor a menor las siguientes cantidades

         3/2       2/3       3/4     4/3



14.