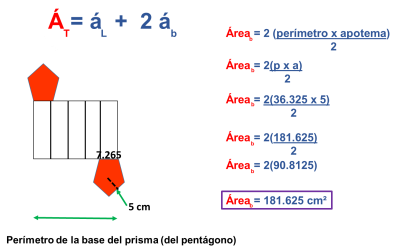MATE 2. Semana del 8 al 12 Enero 2018
Medida
• Justificación de las fórmulas para calcular el volumen de cubos, prismas y pirámides rectos.
Te dejo el siguiente video para que construyas tu cubo y lo lleves a la clase para que te ganes participaciones
Con este video te das cuenta de por qué el volumen de una pirámide es el volumen de un cubo con la misma medida de la base y la misma altura dividido entre 3
• Justificación de las fórmulas para calcular el volumen de cubos, prismas y pirámides rectos.
Te dejo el siguiente video para que construyas tu cubo y lo lleves a la clase para que te ganes participaciones
Con este video te das cuenta de por qué el volumen de una pirámide es el volumen de un cubo con la misma medida de la base y la misma altura dividido entre 3
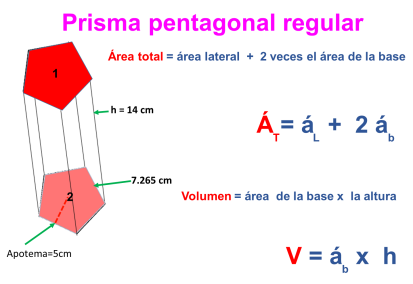
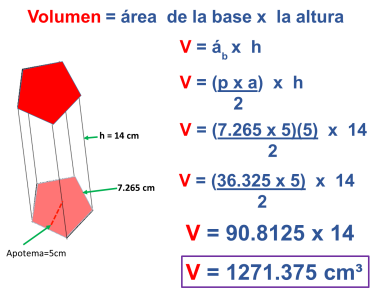
Hallar el área total y el volumen de un prisma pentagonal regular cuya base mide 7.265 de lado y 5 cm de apotema, y la altura el prisma mide 14 cm.
Nos enfocamos en la forma de las bases del prisma para despejar estas fórmulas. El problema indica que es un prisma pentagonal regular con las siguientes medidas.
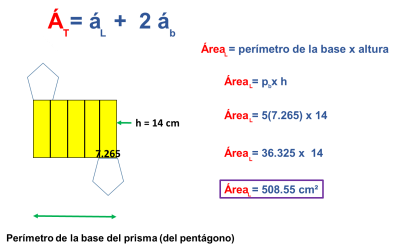
Obtengamos primero el área lateral (el de las cinco caras rectangulares) que es el área coloreada.
Ver vídeo (para recordar cómo se obtiene el área de un rectángulo).
Y ahora el área de las bases. Para ello en la fórmula general vamos a sustituir por la fórmula para obtener el área de un pentágono, ya que la base es pentagonal; y después el resultado se multiplicará por 2 (ya que el prisma tiene dos bases iguales, en este caso, pentágonos regulares). Es el área coloreada.
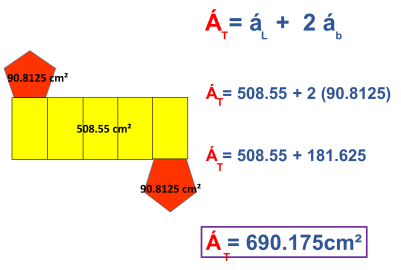
Por último sumaremos los valores del área lateral y del área de las dos bases para obtener el área total del prisma pentagonal regular especificado.
Ahora obtenemos el volumen del prisma pentagonal regular sustituyendo la fórmula del área de la base por la del área del pentágono y multiplicando por la altura del poliedro.
Resuelve los siguientes problemas:
1Halla el área y el volumen de un prisma triangular de altura 6 cm y base un triángulo equilátero de lado 5 cm. Redondea a dos cifras decimales.
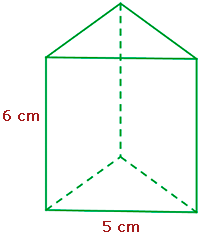

A = cm2
V = cm3
2María regala a su padre un best seller por su cumpleaños. Elige la encuadernación de tapas duras que tiene forma de prisma rectangular, siendo sus medidas 18 cm de largo, 12 cm de ancho y 6 cm de grosor. Si sabemos que al envolverlo un 10% del envoltorio queda oculto por sí mismo, ¿cuál es la cantidad de papel de regalo gastada?


cm2
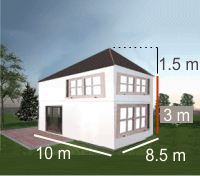
3Calcula el volumen que ocupa la siguiente casa.

V = m3
Calcular el área de la fachada
A = m2
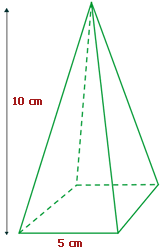
4Calcula el área y el volumen de una pirámide pentagonal de altura 7 cm cuya base es un pentágono regular de 3 cm de lado y apotema 2.06 cm. Redondea a dos cifras decimales.
A = cm2
V = cm3
Calcula la apotema de la pirámide.
Ap = cm
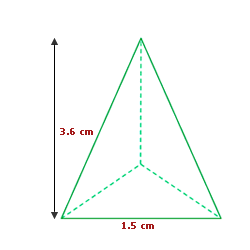
5Una pirámide triangular cuya base es un triángulo equilátero de lado 1.5 cm, tiene una altura de 3.6 cm y la apotema de la base mide 0.43 cm. Calcula el volumen y el área de dicha pirámide redondeando a dos cifras decimales.

A = cm2
V = cm3
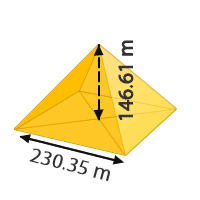
6Por lo general las famosas pirámides de Egipto son pirámides cuadrangulares. La pirámide de Keops es una de las más famosas. Aproximando sus medidas podemos afirmar que tiene por base un cuadrado de lado 230.35 m y una altura de 146.61 m, calcula el volumen que ocupa dicha pirámide. Redondea a dos cifras decimales en los casos que sea necesario.

V = m3
Si quisiésemos cubrir la pirámide de Keops con una tela, ¿qué cantidad de la misma necesitaríamos?
A = m2
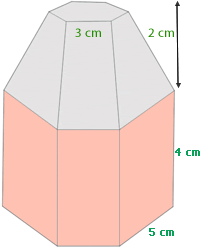
7Calcular la arista de de la pirámide de la siguiente figura.

a = cm
8En el cajón del escritorio Sandra tiene poco espacio y quiere meter una cajita como la de la figura para guardar pendientes. Si el espacio que queda en el escritorio es de 12 cm de ancho, 10 de profundidad y 11 de alto, ¿cabrá la cajita en el escritorio?. Redondea a dos cifras decimales.

Si la parte de la caja del tronco de pirámide es la que corresponde a la tapadera, calcular la cantidad de tela necesaria para forrarla por fuera.
A = cm2