MATE 2. Semana del 27 al 30 Noviembre 2017
Problemas aditivos y TAREA
• Resolución de problemas que impliquen adición y sustracción de monomios
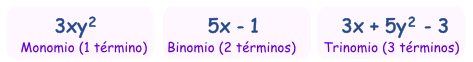
Suma de polinomios vertical
te dejo un link para que practiques la suma y resta de polinomios
• Resolución de problemas que impliquen adición y sustracción de monomios
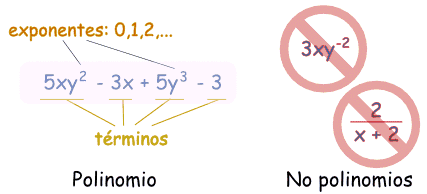
Polinomios
Un polinomio es así: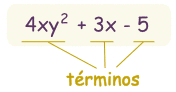 |
| un ejemplo de polinomio este tiene 3 términos |
Están hechos de:
| constantes (como 3, -20, o ½) | |
| variables (como x e y) | |
| exponentes (como el 2 en y2) pero sólo pueden ser 0, 1, 2, 3, ... etc |
Que se pueden combinar usando:
| + - × | sumas, restas y multiplicaciones... |
Estas reglas hacen que los polinomios sean simples, ¡así es fácil trabajar con ellos!
¿Son polinomios o no?

Estos son polinomios:
- 3x
- x - 2
- 3xyz + 3xy2z - 0.1xz - 200y + 0.5
Y estos no son polinomios
- 2/(x+2) no lo es, porque dividir no está permitido
- 3xy-2 no lo es, porque un exponente es "-2" (los exponentes sólo pueden ser 0,1,2,...)
Pero esto sí está permitido:
- x/2 está permitido, porque también es (½)x (la constante es ½, o 0.5)
- también 3x/8 por la misma razón (la constante es 3/8, o 0.375)
Monomios, binomios, trinomios
Hay nombres especiales para los polinomios con 1, 2 o 3 términos:
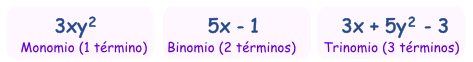
| ¿Cómo te aprendes los nombres? ¡Piensa en bicicletas! |
 |
(También existen cuatrinomio (4 términos) y quintinomio (5 términos), pero se usan poco)
Muchos términos
Los polinomios pueden tener montones de términos, pero no infinitos términos.
¿Qué tienen de especial los polinomios?
Por su definición tan estricta, es fácil trabajar con polinomios.
Por ejemplo sabemos que:
- Si sumas o restas polinomios te sale un polinomio
- Si multiplicas polinomios te sale un polinomio
Así que puedes hacer muchas sumas y multiplicaciones con ellos, y siempre sale un polinomio al final.
Grado
El grado de un polinomio con una sola variable es el mayor exponente de esa variable.
Ejemplo:
| El grado es 3 (el mayor exponente de x) |
Para casos más complicados, lee Grado (de una expresión).
Suma de polinomios horizontal
Suma de polinomios vertical
te dejo un link para que practiques la suma y resta de polinomios
Resta de polinomios
La resta de polinomios consiste en sumar al minuendo el opuesto del sustraendo.
P(x) − Q(x) = (2x3 + 5x − 3) − (2x3 − 3x2 + 4x)
P(x) − Q(x) = 2x3 + 5x − 3 − 2x3 + 3x2 − 4x
P(x) − Q(x) = 2x3 − 2x3 + 3x2 + 5x − 4x − 3
P(x) − Q(x) = 3x2 + x − 3
TAREA
Fecha de entrega: Jueves 30 Noviembre
SUMAS
1)(3x4−2x6+x3−x+5)+(x6−3x2+4x−1)=
2)(2x+3x3−5x3+2x4+5x−1)+(8x3−x4+5x2−9x3)=
3)(2x5−3x4+x3−8x2+2x−7)+(−4+2x2−6x4+x5)=
RESTAS
4)(4x4−3x3+5x4+8x3−4x2+3)−(−5x3−4x4+7+2x2−5x)=
5)(2x7+x5−4x+6x3−2)−(9x3−12x5+2x7−3x3)=
6)(11x2−4x4+8x−9)−(23x4−5x2−6−5x)
RESTAS
