MATE 2. Semana del 27 al 30 abril 2020
|
BLOQUE:
|
2
|
|
EJE:
|
Análisis de datos
|
|
TEMA:
|
Estadística
|
|
SECUENCIA:
|
18. Medidas de tendencia central, rango y desviación media
|
|
LECCIÓN:
|
3. Desviación media
|
|
APRENDIZAJES ESPERADOS:
|
• Usa e interpreta las medidas de tendencia central (moda, media
aritmética y mediana), el rango y la desviación media de un conjunto de datos
y decide cuál de ellas conviene más en el análisis de los datos en cuestión.
|
Desviación media
La desviación media de un conjunto de datos, es la media aritmética de los valores absolutos de lo que se desvía cada valor respecto a la media aritmética.
La fórmula de la desviación media es la siguiente:

Donde:
- x̄: media aritmética de los datos.
- x1, x2, x3, …, xn: datos.
- xi: cada uno de los datos.
- n: número de datos.
Recuerda calcular la media aritmética x̄ antes de aplicar la fórmula de la desviación media. Su fórmula es esta:

La desviación media también es llamada desviación promedio de la media o desviación absoluta promedio. Es una medida de dispersión poco usada debido a la dificultad de hacer cálculos con la función valor absoluto.
Ejemplo 1:
Calcular la desviación media de los siguientes datos: 2, 4, 6 y 8.
Solución:
Empezamos calculando la media aritmética de los datos, teniendo en cuenta que tenemos 4 datos (n = 4).
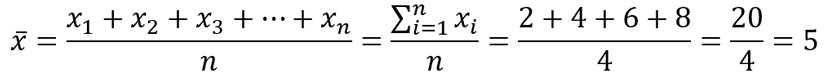
El valor de la media aritmética es de 5.
Ahora aplicamos la fórmula de la desviación media:

El valor de la desviación media, es de 2.
Ejemplo 2:
Calcular la desviación media de los siguientes datos: 3, 5, 8, 6, 2, 4, 7 y 5.
Solución:
Como son muchos datos, vamos a colocar los datos en una tablita:

Sumamos los datos y calculamos su media aritmética, teniendo en cuenta que son 8 datos (n = 8).

Ahora sí, viene el cálculo de la media aritmética.

El valor de la media aritmética es 5.
Agregamos una columna más a la tabla donde colocaremos los valores de xi – μ ó xi - x̄

Agregamos otra columna más a la tabla donde colocaremos los valores de |xi – μ| ó |xi – x̄|

Ahora sí, calculamos la desviación media con los valores obtenidos en la tabla:

El valor de la desviación media es de 1,5.
La desviación media siempre queda expresada en las mismas unidades que los datos originales, por ejemplo, si los datos originales están expresados en kilogramos, pues la desviación media también quedará expresada en kilogramos.
Ejercicios para practicar
Calcula la desviación media de los siguientes datos:
a) 10 cm, 12 cm, 20 cm. Respuesta: D.M. = 4 cm.
b) 12 s, 15 s, 18 s, 17 s. Respuesta: D.M. = 2 s.
Video 1
En el siguiente video, revisaremos la definición de desviación media y resolveremos un primer ejercicio
En este segundo video, resolveremos un ejercicio de desviación media con una mayor cantidad de datos
TAREA PARA ENTREGAR EL JUEVES 30 ABRIL ANTES DE LAS 2:00 PM
CALCULAR LA DESVIACIÓN MEDIA PARA CADA EJERCICIO
2. Número de hermanos que tienen 7 personas:
3, 0, 1, 0, 2, 0, 1
3.
Hallar la desviación media del siguiente conjunto de
datos: 1, 3, 5 y 7.
Respuesta: 2.
4.
Hallar la desviación media del siguiente conjunto de
datos: 2, 3, 6, 11, 13.
Respuesta: 4.
5.
Hallar la desviación media de los siguientes datos: 3,
5, 8, 2, 10, 6, 3, 4, 4 y 5.
Respuesta: 1,8.