MATE 1. Seman del 4 al 8 de mayo 2020
BLOQUE :
|
3
|
EJE:
|
Número, álgebra y variación
|
TEMA:
|
Funciones
|
SUBTEMAS:
|
27. Razón de cambio
|
APRENDIZAJES ESPERADOS
|
Analiza y compara situaciones de variación lineal a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con estos tipos de variación.
|

Intenciones didácticas: A partir de cierta información, que los alumnos construyan tablas y gráficas y que a partir de éstas, relacionen cantidades y obtengan nueva información.
1. Función de proporcionalidad directa
Definición: Se llama función de proporcionalidad directa o, simplemente, función lineal a cualquier función que relacione dos magnitudes directamente proporcionales (x,y).
Su ecuación tiene la forma y = mx
EJEMPLO y = 3x
El factor m (3)es la constante de proporcionalidad y recibe el nombre de pendiente de la función (o razón de cambio), porque indica la inclinación de la recta que la representa gráficamente.
Recuerda: dos magnitudes son directamente proporcionales si su cociente es constante.
Ejemplo si y = 3x entonces (despejamos m de la ecuación, pasamos a la x del otro lado de la igualdad con su operación contraria, es decir, está multiplicando al 3 y pasa al lado contrario dividiendo )
y/x = 3 = m = constante
En la siguiente tabla se muestra el tiempo que ha recorrido un auto y su distancia correspondiente. Nótese que las dos magnitudes (tiempo y distancia) son directamente proporcionales ya que su cociente siempre es igual a 50, por lo que su constante de proporcionalidad k ó m, también llamada pendiente, es igual a 50 como ya lo habíamos calculado.
Definición: Se llama función de proporcionalidad directa o, simplemente, función lineal a cualquier función que relacione dos magnitudes directamente proporcionales (x,y).
Su ecuación tiene la forma y = mx
EJEMPLO y = 3x
El factor m (3)es la constante de proporcionalidad y recibe el nombre de pendiente de la función (o razón de cambio), porque indica la inclinación de la recta que la representa gráficamente.
Recuerda: dos magnitudes son directamente proporcionales si su cociente es constante.
Ejemplo si y = 3x entonces (despejamos m de la ecuación, pasamos a la x del otro lado de la igualdad con su operación contraria, es decir, está multiplicando al 3 y pasa al lado contrario dividiendo )
y/x = 3 = m = constante
En la siguiente tabla se muestra el tiempo que ha recorrido un auto y su distancia correspondiente. Nótese que las dos magnitudes (tiempo y distancia) son directamente proporcionales ya que su cociente siempre es igual a 50, por lo que su constante de proporcionalidad k ó m, también llamada pendiente, es igual a 50 como ya lo habíamos calculado.
|
x
|
Tiempo (horas)
|
1
|
2
|
3
|
4
|
5
|
6
|
|
y
|
Distancia
(km)
|
50
|
100
|
150
|
200
|
250
|
300
|
|
k= m
|
k = y/x
|
50/1= 50
|
100/2= 50
|
150/3= 50
|
200/40= 50
|
250/5= 50
|
300/6= 50
|
Representación gráfica
Como has visto, las funciones lineales se representan gráficamente como líneas rectas. Además, como y=mx, si x=0 entonces y=0; por lo tanto la gráfica de la mayoría de las funciones lineales pasa por el punto (0,0). Para dibujar la gráfica basta con obtener las coordenadas de otro punto, dando un valor arbitrario a la x y unir ese punto con el origen de coordenadas (0,0). Si x=1, entonces y=m, por tanto m representa la variación de la y por cada unidad de x, es decir, la inclinación o pendiente de la recta. Si m es positiva, representa la cantidad que sube la y por cada unidad de x y si m es negativa la cantidad que baja. Como otras funciones, las funciones proporcionales pueden ser descritas y exploradas usando tablas y conjuntos de pares ordenados. Veamos cómo las tablas de funciones proporcionales pueden ser útiles.
Mary trabaja en un puesto cerca de la granja familiar, vendiendo huevos a $1.99 por cartón los fines de semana. Cuando los clientes compran muchos cartones, ella tiene que sumar los totales con lápiz y papel, y le preocupa cometer errores. Por suerte, ésta es una relación proporcional — la salida (costo total) es igual a la entrada (número de cartones) multiplicada por una constante (el precio por cartón). Mary puede usar una función proporcional para obtener una tabla de precios.
Número de cartones
|
Precio total
|
Ahora sólo tiene que utilizar la ecuación para calcular los valores y llenar la tabla. Recuerda,
la ecuación de la función proporcional es y = kx. Por lo que en éste caso,
costo total = precio del cartón • número de cartones.
Costo total = 1.99 • número de cartones = 1.99 x n .
Es decir, y = mx = 1.99xn
donde y = Costo total
1.99 = la constante k ó m
x = número de cartones
|
Número de cartones
|
Precio total
|
|
1
|
1.99x1= $1.99
|
|
2
|
1.99x2= $3.98
|
|
3
|
1.99x3= $5.97
|
|
4
|
1.99x4= $7.96
|
|
5
|
1.99x5= $9.95
|
|
6
|
1.99x6=$11.94
|
Mary puede también escribir las entradas y salidas posibles de ésta función como pares ordenados. Un cartón de huevos cuesta $1.99 y puede ser representado como (1, 1.99). Dos cartones cuestan $3.98, o (2, 3.98), y así sucesivamente.
(1, 1.99)
(2, 3.98)
(3, 5.97)
(4, 7.96)
(5, 9.95)
(6, 11.94)
Nota que en cada par ordenado el valor de y es 1.99 veces el valor de x.
Funciones Proporcionales en Gráficas
Cuando las funciones proporcionales son graficadas, muestran algunas características distintivas — todas las funciones proporcionales son una línea recta que pasa a través del origen la mayoría de la veces.
Grafiquemos la función costo/cartón que hemos estado discutiendo.
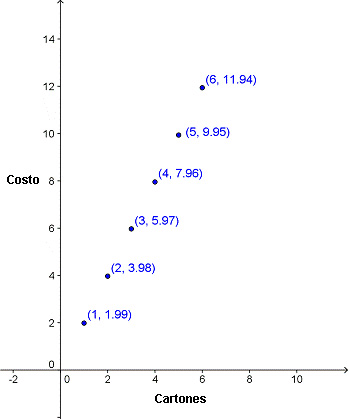
Pero podemos ver que todos los puntos están espaciados de manera uniforme, y aparentemente forman una línea recta. También podemos ver que a pesar de no estar graficado, el punto (0,0) satisface la función — el costo de 0 cartones sería de $0.
Sumario
En una función proporcional, la salida, por ejemplo en el caso de 2 cartones del ejemplo anterior, ( $3.98) es igual a la entrada (2) multiplicada por una constante ($1.99). La constante describe la tasa con la que las variables cambian. Como ésta tasa, o constante de variación, no cambia, las funciones proporcionales tienen una ecuación y una gráfica distintivas. Todas las funciones proporcionales tienen la fórmula y = kx y forman una línea recta que termina o pasa por el origen en la mayoría de los casos.
TAREA PARA ENTREGAR EL VIERNES 8 DE MAYO
| 1.- Los tres hermanos Pérez asistieron al cine. El boleto de entrada cuesta $50.00: a) ¿Cuánto pagaron por las tres entradas? ________________ b) Si cada uno llevó un invitado, ¿cuánto se pagó en total para que todos entraran? _________ c) Si además asistieron los padres de los hermanos Pérez, ¿cuánto se pagó por todos? ______ 1. A partir de la información anterior, completen la siguiente tabla: 2. Con los datos obtenidos en la tabla anterior, tracen la gráfica correspondiente. Observen la gráfica y contesten: a) ¿Cuánto se pagará por cinco personas? _____________ b) ¿Cuánto se pagará por nueve personas? _____________ 2.- Analicen la siguiente gráfica que muestra los cambios en el precio de un artículo durante los primeros meses del año, posteriormente den respuesta a las preguntas a) ¿Cuánto varió el precio del primero al tercer mes? __________________________ b) ¿Cuánto varió el precio del primero al cuarto mes? _________________________ c) Suponiendo que el incremento fue el mismo cada mes, ¿cuánto varió el precio del tercero al sexto mes? _____________________________ d) ¿Cuál es el incremento mensual del precio del artículo? _________________________ e) Si el primer mes corresponde a enero, ¿cuál es el precio del artículo en marzo? __________ f) Si el incremento fue el mismo cada mes, ¿cuál será el precio del artículo en diciembre? ________________________ g) Respecto al inciso a, encuentren el cociente del incremento en el precio entre el número de meses, es decir la “razón de cambio”. Encuentren la razón de cambio en los incisos b y c y compárenla con la del inciso a. ¿Cómo son? ________________________________________ RECUERDEN QUE LA RAZÓN DE CAMBIO SE OBTIENE POR MEDIO DE:
|
6. Para pintar un edificio de departamentos, se necesita comprar pintura de diferentes colores, si con el tipo de pintura seleccionada se cubren 24 m2 por cada 4 litros:
a) Anoten las cantidades que faltan en la tabla.
m2
|
30
|
48
|
72
|
120
|
180
|
240
|
litros
|
b)¿Qué expresión algebraica permite conocer la cantidad de litros cuando se conoce el número de metros cuadrados por cubrir? _______
Dibujo de sucesiones