MATE 2. Semana del 6 al 10 de mayo 2019
|
BLOQUE
| IV |
|
EJE:
|
Número, álgebra y variación
|
|
TEMA:
|
Patrones, figuras geométricas y expresiones equivalentes
|
|
Subtema
|
• Construcción de sucesiones de números enteros a partir de las
reglas algebraicas que las definen. Obtención de la regla general (en
lenguaje algebraico) de una sucesión con progresión aritmética de números
enteros
|
|
APRENDIZAJES ESPERADOS:
|
• Representa sucesiones de números enteros a partir de una regla dada
y viceversa.
|
1. Concepto de sucesión
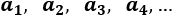
Ejemplo
Un ejemplo de sucesión es el conjunto de los números pares: 2, 4, 6, 8, 10, 12, 14,...
Ejemplo
En la sucesión de las pares, el primer término es y el sexto es . El término general es2. Sucesión aritmética
Una sucesión es aritmética cuando cada término se obtiene sumando un número al término que le precede. Este número se denomina diferencia y se denota por .
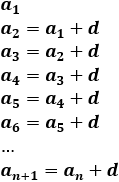
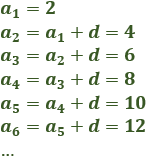 La diferencia se calcula restando dos términos consecutivos:
La diferencia se calcula restando dos términos consecutivos:
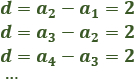
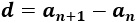 Es decir, la diferencia se obtiene restando términos consecutivos.
Es decir, la diferencia se obtiene restando términos consecutivos.
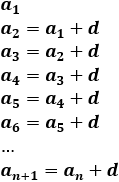
Ver ejemplo
Ejemplo
La sucesión de los números pares es aritmética con diferencia ya que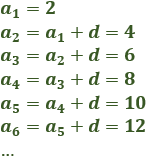
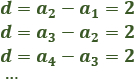
Fórmula para calcular la diferencia:
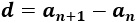
Si la diferencia entre dos términos consecutivos no es constante en toda la sucesión, entonces la sucesión no es aritmética.
4. Término general
Se puede calcular cualquier término de la sucesión mediante una fórmula (fórmula o término general). Esta fórmula se obtiene a partir del primer término y de la diferencia:
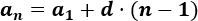
Como el primer término es y la diferencia es , el término que ocupa la décima posición es
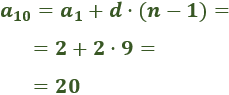
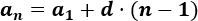
Ver ejemplo
Ejemplo
Calculamos el término 10-ésimo de la sucesión de los pares.Como el primer término es y la diferencia es , el término que ocupa la décima posición es
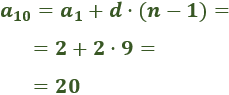
TAREA PARA ENTREGAR EL JUEVES 9
Problema 1
Calcular la diferencia de las siguientes sucesiones:
- 11, 13, 15, 17, 19,...
- 11, 16, 21, 26, 31,...
- 10, 6, 2, -2, -6, -10,...
Problema 2
¿Cuál de las siguientes sucesiones no es aritmética?
- 16, 26, 36, 46,...
- 16, 6, 13, 3,...
- -26, -36, - 46, -56,...
Problema 3
¿Cuál es el segundo término de la siguiente sucesión aritmética?
Problema 4
Calcular los dos siguientes términos de las sucesiones aritméticas:
- 45, 55, 65,...
- 11, 22, 33,...
- 87, 76, 65,...
¿Cuál es la diferencia de estas sucesiones?
Problema 5
Si dos sucesiones tienen la misma diferencia, ¿son la misma sucesión?
Problema 6
Determinar si las siguientes sucesiones son crecientes o decrecientes:
- 20, 15, 10, 5,...
- -3, -6, -9, -12,...
- 4, 14, 24, 34,...
Problema 7
Calcular el término de cada sucesión:
- 8, 14, 20, 26,...
- 4, 10, 16, 22,...
- 8, 5, 2, -1,...
Problema 8
Calcular el término de cada sucesión a partir de los datos proporcionados:
Determinar si las sucesiones son crecientes o decrecientes.
Problema 9
Calcular el término general de las siguientes sucesiones:
- 6, 13, 20, 27,...
- 6, 2, -2, -6,...
- 0, -1/2, -1, -3/2,...