MATE 3. Semana del 7 al 11 de enero 2019

Bloque:	3
Eje:	Sentido numérico y pensamiento algebraico
TEMA:	Patrones y ecuaciones
APRENDIZAJES ESPERADOS	• Resolución de problemas que implican el uso de ecuaciones cuadráticas. Aplicación de la fórmula general para resolver dichas ecuaciones

Ecuación cuadrática

Esto es una ecuación cuadrática:

(a, b, y c pueden tener cualquier valor, excepto que a no puede ser 0.)

La letra "x" es la variable o incógnita, y las letras a, b y c son los coeficientes (lee las Definiciones básicas de Álgebra)

Y el nombre cuadrática viene de "cuad" que quiere decir cuadrado, porque el exponente más grande es un cuadrado (en otras palabras x2).

Ejemplos de ecuaciones cuadráticas:

		En esta a=2, b=5 y c=3
		Aquí hay una un poco más complicada: ¿Dónde está a? En realidad a=1, porque normalmente no escribimos "1x2" b=-3 ¿Y dónde está c? Bueno, c=0, así que no se ve.
		¡Ups! Esta no es una ecuación cuadrática, porque le falta el x2 (es decir a=0, y por eso no puede ser cuadrática)

¿Qué tienen de especial?

Las ecuaciones cuadráticas se pueden resolver usando una fórmula especial llamada fórmula cuadrática:

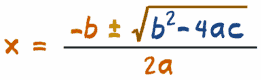
	El "±" quiere decir que tienes que hacer más Y menos, ¡así que normalmente hay dos soluciones!
	La parte azul (b2 - 4ac) se llama discriminante, porque sirve para "discriminar" (decidir) entre los tipos posibles de respuesta: si es positivo, hay DOS soluciones si es cero sólo hay UNA solución, y si es negativo hay dos soluciones que incluyen números imaginarios .

Solución

Para resolverla, sólo pon los valores de a,b y c en la fórmula cuadrática y haz los cálculos.

Ejemplo: resuelve 5x² + 6x + 1 = 0

Fórmula cuadrática: x = [ -b ± √(b²-4ac) ] / 2a

Los coeficientes son: a = 5, b = 6, c = 1

Sustituye a,b,c: x = [ -6 ± √(6²-4×5×1) ] / 2×5

Resuelve: x = [ -6 ± √(36-20) ]/10 = [ -6 ± √(16) ]/10 = ( -6 ± 4 )/10

Respuesta: x = -0.2 and -1

(Comprobación:
5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 = 0.2 -1.2 + 1 = 0
5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 + 1 = 0)

Ecuaciones cuadráticas disfrazadas

Algunas ecuaciones no parece que sean cuadráticas, pero con manipulaciones astutas se pueden transformar en una:

Disfrazadas	Qué hacer	En forma estándar	a, b y c
x2 = 3x -1	Mueve todos los términos a la izquierda	x2 - 3x + 1 = 0	a=1, b=-3, c=1
2(x2 - 2x) = 5	Desarrolla paréntesis	2x2 - 4x - 5 = 0	a=2, b=-4, c=-5
x(x-1) = 3	Desarrolla paréntesis	x2 - x - 3 = 0	a=1, b=-1, c=-3
5 + 1/x - 1/x2 = 0	Multiplica por x2	5x2 + x - 1 = 0	a=5, b=1, c=-1

Ejemplo
Problema	Usar la fórmula cuadrática para resolver la ecuación
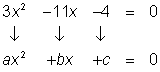			a = 3, b = -11,  c = -4 Nota que la resta de signos significa que los coeficientes b y c son negativos
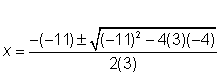			Sustituir los valores en la fórmula cuadrática
			Simplificar, teniendo cuidado con los signos
			Simplificar más
			Simplificar el radical: .
	o		Separar y simplificar para encontrar las soluciones de la ecuación cuadrática. Nota que en una, 13 es sumado y en la otra, 13 es restado
Solución	x = 4 o

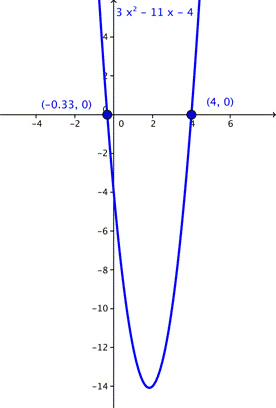
La solución para la ecuación cuadrática nos da las coordenadas en x de las intersecciones en x, o las raíces de una ecuación cuadrática. Las raíces de la ecuación cuadrática son los valores donde la parábola cruza el eje x. Podemos comprobar esto observando la gráfica de la función 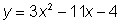 y ver que las raíces son (4, 0) y (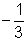, 0).

Ejemplo
Problema	Usar la fórmula cuadrática para resolver la ecuación
			Restar 6x de cada lado y sumar 16 a ambos lados para transformar la ecuación a su forma.
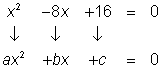			Identificar los coeficientes a, b, y c. x2= 1x2, entonces a = 1. Como 8x está siendo restado, b es negativo. a = 1, b = -8, c = 16.
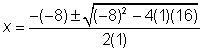			Aplicar la fórmula cuadrática
			Simplificar
			Como la raíz cuadrada de 0 es 0, y sumar o restar 0 dan el mismo resultado, existe sólo un valor posible
Solución	x = 4

Esta ecuación cuadrática sólo tiene una solución, por lo que la gráfica de la función 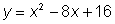 tocará el eje x una vez. Tiene una sola raíz.

Sumario

La fórmula cuadrática, 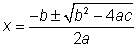, se obtiene al completar el cuadrado de la ecuación cuadrática .  La fórmula puede ser usada para encontrar la solución de una ecuación cuadrática e identificar cualquier raíz posible, o las intersecciones en x, de la función.

El discriminante de una fórmula cuadrática es la cantidad debajo del radical , 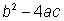. Determina cuántas soluciones existen para la ecuación cuadrática. Si el discriminante es positivo, hay dos raíces. Si es cero, existe una raíz. Si el discriminante es negativo, no existen raíces.

TAREA PARA ENTREGAR EL VIERNES 11 DE  ENERO

1.- Seth resolvió una ecuación cuadrática. Su trabajo, sin el paso $3$, se muestra a continuación.

¿Qué pudo haber escrito Seth como resultado del paso $3$?

$\begin{aligned} \dfrac{1}{2}(x-1)^2+5&=23 \\\\ \dfrac{1}{2}(x-1)^2&=18&\text{Paso }1. \\\\ (x-1)^2&=36&\text{Paso }2. \\\\ &&\text{Paso }3. \\\\ x=-5&\text{ o }x=7&\text{Paso }4. \end{aligned}$

Escoge 1 respuesta:

Escoge 1 respuesta:

• 
  

  
  

  
  

  $x^2=35$
• 
  

  
  

  
  

  $x^2-1=36$
• 
  

  
  

  
  

  $x^2=36$
• 
  

  
  

  
  

  $x-1=\pm6$

2.- Mitchell resolvió una ecuación cuadrática. Su trabajo se muestra a continuación.

¿En qué paso Mitchell cometió un error?

$\begin{aligned} 5(x-2)^2+6&=86 \\\\ 5(x-2)^2&=80&\text{Paso }1. \\\\ (x-2)^2&=16&\text{Paso }2. \\\\ x^2-2^2&=16&\text{Paso }3. \\\\ x^2&=20&\text{Paso }4. \\\\ x&=\pm\sqrt{20}&\text{Paso }5. \end{aligned}$

Escoge 1 respuesta:

Escoge 1 respuesta:

• 
  

  
  

  
  

  $\text{Paso } 2$
• 
  

  
  

  
  

  $\text{Paso } 3$
• 
  

  
  

  
  

  $\text{Paso } 4$
• 
  

  
  

  
  

  $\text{Paso } 5$

3.- Tara resolvió una ecuación cuadrática. Su trabajo, sin el paso 2, se muestra a continuación.

¿Qué pudo haber escrito Tara como resultado del paso $2$?

$\begin{aligned} 2(x-3)^2+6&=14 \\\\ 2(x-3)^2&=8&\text{Paso }1. \\\\ &&\text{Paso }2. \\\\ x-3&=\pm 2&\text{Paso }3. \\\\ x=1&\text{ o }x=5&\text{Paso }4. \end{aligned}$

Escoge 1 respuesta:

Escoge 1 respuesta:

• 
  

  
  

  
  

  $(x-3)^2=6$
• 
  

  
  

  
  

  $(x-3)^2=4$
• 
  

  
  

  
  

  $x^2-3^2=8$
• 
  

  
  

  
  

  $x-3=4$

4

Determinar el tipo y número de soluciones de la ecuación

5

Determinar el tipo y número de soluciones de la ecuación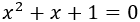

6.- Resolver la ecuación de segundo grado incompleta

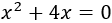
Problema 7

Encontrar las raíces de la función polinómica de segundo grado

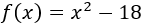
Problema 8

Resolver la ecuación de segundo grado completa

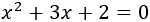
Problema 9

Resolver la ecuación

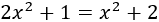
Problema 10

Resolver la ecuación completa

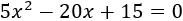
Aplicando la fórmula general resuelve las siguientes ecuaciones cuadráticas

1Solución

2

3

4

5

6 x² + (7 − x)² = 25

        

7.-Los tres lados de un triángulo rectángulo son proporcionales a los números 3, 4 y 5. Halla la longitud de cada lado sabiendo que el área del triángulo es 24 m².

8.- Un jardín rectangular de 50 m de largo por 34 m de ancho está rodeado por un camino de arena uniforme. Halla la anchura de dicho camino si se sabe que su área es 540 m².

9.- Halla un número entero sabiendo que la suma con su inverso es 

Reactivos tipo PLANEA

.