MATE 2. Semana del 16 al 19 octubre 2018
FORMA, ESPACIO Y MEDIDA.
• Resolución de problemas que impliquen el cálculo de áreas de figuras compuestas, incluyendo áreas laterales y totales de prismas y pirámides



TAREA PARA ENTREGAR EL JUEVES 18
1.- Hallar el área total y el volumen de un prisma triangular cuya base mide 10 x 43 y con una altura de 42 cm; si la altura el prisma mide 60 cm.
2.- Hallar el área total y el volumen de un prisma cuadrangular regular cuyo lado de la base mide 1.20 m y la altura de 4 m.
3.- Hallar el área total y el volumen de un prisma cuadrangular irregular cuya base mide 38 cm por 21 cm y la altura del prisma es de 30 cm.
4.- Hallar el área total y el volumen de un prisma pentagonal regular cuya base mide 7.265 de lado y 5cm de apotema, y la altura el prisma mide 14 cm.

7. Encuentre el área total de la superficie de una pirámide regular con una base cuadrada para cada lado de la base mide 16 pulgadas, la altura de la inclinación de un lado es de 17 pulgadas y la altitud es de 15 pulgadas.

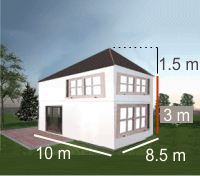
8. Calcula el volumen que ocupa la siguiente casa.
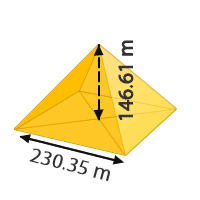
9. Por lo general las famosas pirámides de Egipto son pirámides cuadrangulares. La pirámide de Keops es una de las más famosas. Aproximando sus medidas podemos afirmar que tiene por base un cuadrado de lado 230.35 m y una altura de 146.61 m, calcula el volumen que ocupa dicha pirámide. Redondea a dos cifras decimales en los casos que sea necesario.
• Resolución de problemas que impliquen el cálculo de áreas de figuras compuestas, incluyendo áreas laterales y totales de prismas y pirámides

1.1- El prisma
Los prismas son poliedros que tienen:

1.2- La pirámide
Es una figura tridimensional constituida por una base poligonal y por caras laterales cuyas aristas concurren a un punto del espacio llamado cúspide o vértice común, por lo tanto las caras laterales siempre serán triangulares. El eje o altura de la pirámide es la línea que va del vértice al centro de la base.
Es una figura tridimensional constituida por una base poligonal y por caras laterales cuyas aristas concurren a un punto del espacio llamado cúspide o vértice común, por lo tanto las caras laterales siempre serán triangulares. El eje o altura de la pirámide es la línea que va del vértice al centro de la base.
La apotema lateral de una pirámide regular es la altura de cualquiera de sus caras laterales.

Área y volumen de un prisma.
Para calcular el área total de un prisma siempre es necesario conocer tres medidas:
- El área de una base.
- El perímetro de la base
- La altura del prisma
Las fórmulas generales para obtener el área y el volumen de cualquier prisma son las siguientes:
TAREA PARA ENTREGAR EL JUEVES 18
1.- Hallar el área total y el volumen de un prisma triangular cuya base mide 10 x 43 y con una altura de 42 cm; si la altura el prisma mide 60 cm.
2.- Hallar el área total y el volumen de un prisma cuadrangular regular cuyo lado de la base mide 1.20 m y la altura de 4 m.
3.- Hallar el área total y el volumen de un prisma cuadrangular irregular cuya base mide 38 cm por 21 cm y la altura del prisma es de 30 cm.
4.- Hallar el área total y el volumen de un prisma pentagonal regular cuya base mide 7.265 de lado y 5cm de apotema, y la altura el prisma mide 14 cm.
5- El área total de una pirámide cuya base es un rectángulo de lados 5cm y 11 cm, y su apotema cm, es igual a:
A- 183 cm2 B- 203 cm2 C- 220 cm2 D- 440 cm2
6. Encuentre el área lateral de la superficie de una pirámide regular con una base triangular si cada uno mide la longitud de la inclinación de 5 pulgadas.

7. Encuentre el área total de la superficie de una pirámide regular con una base cuadrada para cada lado de la base mide 16 pulgadas, la altura de la inclinación de un lado es de 17 pulgadas y la altitud es de 15 pulgadas.

8. Calcula el volumen que ocupa la siguiente casa.

V = m3
Calcular el área de la fachada
A = m2
9. Por lo general las famosas pirámides de Egipto son pirámides cuadrangulares. La pirámide de Keops es una de las más famosas. Aproximando sus medidas podemos afirmar que tiene por base un cuadrado de lado 230.35 m y una altura de 146.61 m, calcula el volumen que ocupa dicha pirámide. Redondea a dos cifras decimales en los casos que sea necesario.

V = m3
