MATE 1. Semana del 15 al 19 octubre 2018
ÁNGULOS FORMADOS POR DOS RECTAS PARALELAS Y UNA SECANTE
Recta secante
Es una línea transversal que corta dos o mas rectas.
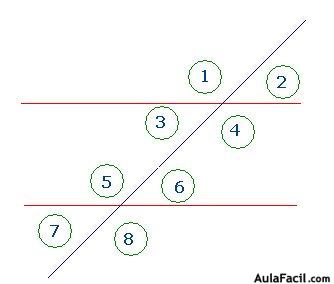
Cuando dos rectas paralelas son cortadas por una secante (S,S´), se forman ocho ángulos; como se muestra en la siguiente figura:

Los ocho ángulos que se forman de las dos rectas paralelas y la secante se denominan:
1.- Ángulos internos: son cuatro y son los ángulos: 3,4,5 y 6
2.- Ángulos externos: también son cuatro y los conforman los ángulos: 1,2,7 y 8
Los anteriores ángulos también se clasifican en:
1.- Ángulos alternos internos: los ángulos internos son también llamados no adyacentes, (son iguales), se ubican de los dos lados de la secante y son los ángulos: (3 y 5),(4 y 6)
2..- Ángulos alternos externos: ángulos externos no adyacentes, (son iguales) y también son situados en distinto lado de la secante, son los ángulos: (1 y 7), (2 y 8)
3.- Ángulos correspondientes: son los dos ángulos no adyacentes, (son iguales), se ubican en el mismo lado de la secante y son los ángulos: (1 y 5), (4 y 8), (2 y 6), (3 y 7)
4.- Ángulos conjugados o colaterales: son ángulos suplementarios (su suma es de 180°) pueden ser dos ángulos internos o dos externos, están situados del mismo lado de la secante. Los ángulos conjugados internos son: (3 y 6), (4 y 5); y los ángulos conjugados externos son: (2 y 7), (1 y 8).
Se sabe que de los ocho ángulos:
*Cuatro son agudos e iguales entre sí: el ángulo 2,4,6,8
*Cuatro son obtusos y también iguales entre sí: el ángulo 1,3,5,7.
Ejemplo 1:
En la siguiente gráfica halla los valores de "x" y "y", según la clasificación de los pares de ángulos cortados por una secante entre dos rectas.

1. Por ser ángulos alternos internos: el ángulo de 130° es igual que el ángulo x; por lo tanto x=130°
2. Por ser ángulos correspondientes: el ángulo x+y= 180°, por lo tanto: x=130°
Sustituyendo la expresión anterior, tenemos que:
130°+y=180°
y=180°-130°
y=50°
Obteniendo como resultado que: X=130° y Y=50°
Por si aún queda duda, aquí está este otro ejemplo:
Ejemplo 2:
En la siguiente gráfica halla el valor de "x" y "y"...

olución:
1. Por ser ángulos alternos internos: X=30°
2. La figura contiene a un triángulo cuya suma de sus ángulos interiores es 180°, por lo que: x+y+70°= 180°
Por lo tanto si se conoce que x=30°
Sustituyendo los valores de x en la ecuación anterior tenemos que:
30+y+70°=180°
y=180°-130°
y=50°
Finalmente, el ángulo X=30° y el ángulo Y=80°
1. Por ser ángulos alternos internos: X=30°
2. La figura contiene a un triángulo cuya suma de sus ángulos interiores es 180°, por lo que: x+y+70°= 180°
Por lo tanto si se conoce que x=30°
Sustituyendo los valores de x en la ecuación anterior tenemos que:
30+y+70°=180°
y=180°-130°
y=50°
Finalmente, el ángulo X=30° y el ángulo Y=80°
olución:
1. Por ser ángulos alternos internos: X=30°
2. La figura contiene a un triángulo cuya suma de sus ángulos interiores es 180°, por lo que: x+y+70°= 180°
Por lo tanto si se conoce que x=30°
Sustituyendo los valores de x en la ecuación anterior tenemos que:
30+y+70°=180°
y=180°-130°
y=50°
Finalmente, el ángulo X=30° y el ángulo Y=80°
Clasificación de ángulos según su medida
2 Tipos de ángulos según su posición
3 Clases de ángulos según su suma
4 Ángulos entre paralelas y una recta transversal
Relaciones entre parejas de ángulos
En casi todas las figuras geométricas donde intervengan rectas aparecen ángulos, los cuales es posible relacionar en cuanto a sus dimensiones y a su posición en el plano.
Así, dos ángulos pueden ser entre sí complementarios, suplementarios o adyacentes.
1 + 2= 90°

Dos ángulos son suplementarios si la suma de sus medidas es 180°1 + 2 son complementarios, ya que:
1 + 2= 180°
1 + 2= 180°


Como ya vimos, por definición, un ángulo es una figura geométrica formada en una superficie por dos líneas rectas que parten de un mismo punto.
Fijando nuestra atención en las rectas, sabemos que estas pueden ser secantes (que se cortan) o paralelas (que no se cortan nunca).
Dos rectas secantes se cortan en un punto y determinan cuatro ángulos. Cada ángulo tiene dos lados y un vértice.

Ángulos opuestos por el vértice.
Son los ángulos formados por dos rectas que se cortan en un punto llamado vértice (V).
Los ángulos opuestos por el vértice son iguales.

Si el angulo # 1 mide 45 grado, entonces el angulo # 2 también tiene 45 grado, ya que los dos son apuesto por el vértice.
< 1 = < 2
< 3 = < 4
Ángulos determinados por dos rectas paralelas y una secante.
Cuando dos rectas paralelas es cortadas por una tercera recta secante, se forman 8 ángulos,

Esta distribución permite caracterizar parejas de ángulos según su posición, haciendo notar que los ángulos 3, 4, 5, y 6 son internos y que los ángulos 1, 2, 7, 8 son externos.

También se puede deducir que:
-Los ángulos 1 y 5 son correspondientes.
-Los ángulos 1 y 5 son correspondientes.
-Los ángulos 1 y 3 son opuesto.
-Los ángulos 1 y 2 son adyacentes.
-Los ángulos 5 y 8 son opuesto.
-Los ángulos 5 y 6 son adyacentes.
...y así sucesivamente.
TAREA PARA ENTREGAR EL JUEVES 11
Dadas las rectas p y q cortadas por la transversal r y las medidas de los ángulos dados
Hallar:
1-) Si medida de angulo g = 125°......... m
encontrar las medidas de los demás ángulos.
Hallar:
2-) Si medida de angulo a = 75°......... m
encontrar las medidas de los demás ángulos.

3. Observa la figura siguiente y después, contesta a las preguntas siguientes:
- ¿Cómo son los ángulos 1 y 2?
- ¿Cómo podemos llamar a los ángulos 1 y 4?
- ¿Son suplementarios los ángulos 2 y 4?
- ¿Son iguales los ángulos 2 y 3? ¿Por qué?
- ¿Son correspondientes los ángulos 3 y 7?
- ¿Cómo son los ángulos 4 y 6?
- ¿Es el ángulo 6 correspondiente al ángulo 3?
- ¿Son iguales los ángulos 5 y 8? ¿Por qué?
- ¿Cómo puedes llamarles a los ángulos 1 y 8?
- ¿Son alternos internos los ángulos 5 y 6?
Relaciona cada ángulo al lugar que corresponda:







Convexo
Llano
Cóncavo
Elige la opción correcta:
3Dos ángulos adyacentes son los que...
4Un ángulo obtuso...
5Un ángulo agudo...
6Si tenemos cuatro ángulos opuestos por el vértice y uno de ellos mide 60°, los otros tres miden respectivamene...
7Los ángulos...

8Los ángulos...

Completa según se indique:
9El ángulo complementario de 57°.
º
10El ángulo complementario de 35° 25' 56''.
º'''
Completa según se indique:
11El ángulo suplementario de 123°.
º
12El ángulo suplementario de 35° 25' 56''